«Виртуальная» Нобелевская премия по химии (2013)
10 октября 2013
«Виртуальная» Нобелевская премия по химии (2013)
- 1521
- 0
- 1
Центральной метафорой Нобелевской премии по химии 2013 года стало символическое «примирение» Ньютона с котом Шредингера :-)
пресс-релиз Нобелевского комитета
-
Автор
-
Редакторы
Темы
Статья на конкурс «био/мол/текст»: Не так давно закончились те славные времена, когда химики и молекулярные биологи «собирали» молекулы из пластикового конструктора. Сегодня для этих целей используется компьютер, причем в виртуальной «кремниевой» реальности (in silico) можно моделировать не только структуру, но и функции биологических молекул, и даже протекание химических реакций. Нобелевская премия по химии в 2013 году вручена Мартину Карплюсу, Майклу Левитту и Ариэ Варшелю за то, что они заложили фундамент для химического и структурного моделирования биологических молекул.
Конкурс «био/мол/текст»-2013
Эта статья представлена на конкурс научно-популярных работ «био/мол/текст»-2013 в номинации «Лучшее новостное сообщение».
Спонсор конкурса — дальновидная компания Thermo Fisher Scientific. Спонсор приза зрительских симпатий — фирма Helicon.
Химия (а точнее, биохимия) совершила в последние 50–60 лет невиданный скачок, и одним из ярчайших достижений стало определение пространственной структуры белков. Стандартные методы анализа строения белков — рентгеновская кристаллография и спектроскопия ядерного магнитного резонанса [1] — уже давно оперируют такими объемами информации, что не могли бы существовать без компьютеров и соответствующего программного обеспечения. Однако не многим известно, что основу этого программного обеспечения составляют алгоритмы расчета энергии изучаемой структуры, которые, в свою очередь, опираются на эмпирические и теоретические потенциалы взаимодействия между атомами. Вот так компьютеры и теоретические модели и стали важным подспорьем биохимиков-экспериментаторов.
История использования теоретических моделей в химии восходит своими корнями в середину ХХ века, когда были совершены два революционных открытия: после многолетних поисков были обнаружены принципы организации структуры белков и нуклеиновых кислот [2].
Но наука не стоит на месте, и в наши дни акцент химических исследований переносится со структуры на функцию. Вместо вопроса «что это такое?» все чаще звучит вопрос «как это работает?», и на этот вопрос дать ответ значительно труднее. Дело в том, что современные экспериментальные методы — такие как изотопное мечение или фемтосекундная спектроскопия — могут дать какие-то подсказки относительно механизма реакции, но едва ли они способны до конца объяснить столь сложные процессы, как, например, биохимические. И тут на помощь снова приходит теоретическое рассмотрение. Дело в том, что одним из важнейших понятий в теории химических реакций является переходное состояние — такая конфигурация атомов, которая является промежуточной между реагентами и продуктами и обладает при этом минимально возможной (свободной) энергией. Это состояние обычно не может быть обнаружено экспериментально, зато теория предлагает несколько методов изучения подобных структур. И мы снова видим, как теория приходит на помощь эксперименту.
Работа, за которую в этом (2013-м) году присуждена Нобелевская премия по химии, посвящена методам моделирования больших и сложных химических систем и реакций с помощью как классической, так и квантово-механической теории. Сейчас такой обоюдный подход воспринимается уже как нечто само собой разумеющееся, но именно он и является главной заслугой лауреатов. В то время как квантовохимические модели нацелены на описание электронов и ядер атомов, классические модели рассматривают атомы и группы атомов как целое, и поэтому они имеют гораздо меньше степеней свободы и могут быть гораздо быстрее обработаны с помощью компьютера. Более того, физические принципы, лежащие в основе классической модели, гораздо проще, и это тоже вносит свою лепту в ускорение расчетов. Стоило большого труда разработать такой подход, который позволял бы для центральной части системы использовать квантовохимическое описание, остальную часть системы описывать с классической точки зрения и физически осмысленно связывать эти части между собой. Кроме того, как-то надо описать окружение и всей системы в целом. Для этого часто ее помещают в диэлектрическую среду (рис. 1).
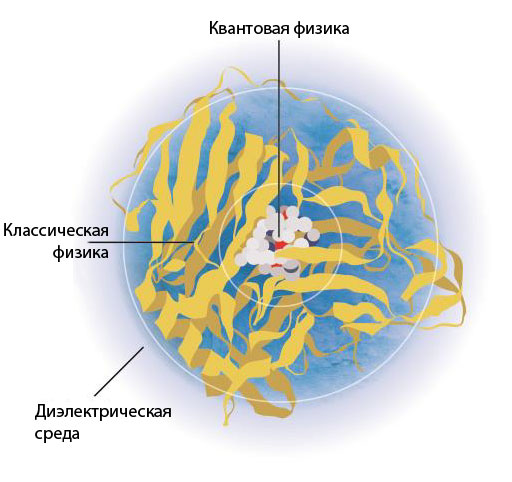
Рисунок 1. Медная оксидаза в водном окружении. Разделение системы на концентрические сферы иллюстрирует области, рассматриваемые с разной степенью физической достоверности: центральная часть моделируется наиболее достоверно (с помощью квантовой механики), окружающие атомы белка и растворитель — методами классической механики, а совсем удаленные области не включают явного описания атомов, а лишь усредненный параметр среды (диэлектрическую проницаемость).
Как все начиналось
Описанное выше теоретическое моделирование опирается, главным образом, на четыре группы работ. Центральная часть системы (рис. 1; атомы окрашены серым и красным) описывается квантово-химическими методами, за разработку которых Вальтер Кон (Walter Kohn) и Джон Попл (John Pople) получили Нобелевскую премию в 1998 году. Квантовая механика, на которую опирается квантовая химия, была разработана за 75 лет до того и принесла пять Нобелевских премий в период с 1918 по 1933 год. Лауреатами стали Макс Планк в 1918, Нильс Бор в 1922, Луи де Бройль в 1929, Вернер Гейзенберг в 1932 и Эрвин Шредингер с Полем Дираком в 1933.
Описание остальной части системы имеет не менее славную предысторию. Прежде всего, необходимо было ввести потенциал межмолекулярного взаимодействия в такого рода моделях. Это также было сделано в докомпьютерную эру — в 1946 году — тремя независимыми группами исследователей [3–5], которые взяли за основу потенциал Кулона (электростатический потенциал) и потенциал Ван-дер-Ваальса. (Кстати, сам Ян Дидерик Ван-дер-Ваальс тоже стал лауреатом Нобелевской премии по физике в 1910 году.) Со временем оказалось, что наибольших успехов удалось добиться группе Фрэнка Уэстхаймера (Frank Westheimer). Появление компьютеров придало новый импульс работам в этой области. Норман Эллинджер (Norman Allinger) разработал программу для оптимизации структуры молекул с использованием этих классических потенциалов. Такой подход получил название молекулярной механики [6] и стал применяться для изучения систем органических молекул.
Подробно про метод молекулярной механики «Биомолекула» уже писала: «Молекулярная динамика биомолекул. Часть I. История полувековой давности» [8].
Параллельным путем пошли Джордж Немети (George Nemethy) и Гарольд Шерага (Harold Scheraga) [7]. Вдохновившись идеями Уэстхаймера и Эллинджера, они разработали упрощенную версию потенциалов взаимодействия и использовали их при оптимизации структуры белков. Примерно в это же время для создания меж- и внутримолекулярных потенциалов стали использоваться и квантово-химические методы. Здесь лидерство захватили Шнеир Лифсон (Shneior Lifson) и Ариэ Варшель (Arieh Warshel), разработавшие метод согласованного силового поля (Consistent Force Field, CFF) [8], [9]. Майкл Левитт (Michael Levitt) и Ш. Лифсон стали первыми, кто использовал этот метод для минимизации энергии белка [10].
Достоинством методов, использующих классические потенциалы, является относительная легкость расчета энергии и возможность изучения больших систем. Недостатком же является необходимость рассматривать лишь небольшие изменения в структурах взаимодействующих молекул, поэтому такие методы не могут применяться для изучения химических реакций, в которых происходит образование новых молекул.
Напротив, квантовохимические методы могут с успехов применяться для изучения химических реакций, т.е. процессов разрушения одних молекул и образования других, но эти методы являются очень ресурсоемкими и подходят для изучения лишь небольших систем.
Если считать, что задача создания потенциальной функции для описания окружения решена, то остается решить вопрос с описанием конформации этого окружения. Тут снова есть два пути решения: первый был использован Эллинджером в его молекулярно-механических методах и состоял в минимизации энергии системы и создании одной характерной конформации; второй был предложен Немети и Шерагой и состоял в использовании методов статистической механики, таких как молекулярная динамика (МД) [8], [11] или метод Монте Карло (МК) [11] для создания множества конфигураций с правильными статистическими весами.
Важность работы лауреатов не зависит от того, какая стратегия используется для выбора изучаемой конформации. Разработанная теория указывает, как аккуратно и эффективно оценивать изменения энергии в таких реальных системах, где значительные перестройки геометрии или изменение электронного состояния в небольшой части изучаемой системы сопряжено со слабо изменяющимся окружением. Одним из путей решения этой проблемы является создание эффективной компьютерной программы, основанной на уравнении Шредингера и способной работать с системами любого требуемого размера. Перспективным направлением на этом пути является метод Кар-Паринелло [12], но и он является слишком требовательным к компьютерным ресурсам, когда речь заходит о расчете биомолекулярных и супрамолекулярных систем с требуемой точностью. Другим путем является сочетание классического подхода к моделированию окружения на основе работ Уэстхаймера [3], Эллинджера [6] и Немети и Шераги [7] с квантовохимическим подходом к моделированию центральной области, где и происходит интересующая химическая реакция.
Вклад нынешних лауреатов
Первый шаг на пути к созданию мультимасштабного моделирования был сделан, когда Ариэ Варшел (Arieh Warshel) посетил Мартина Карплюса (Martin Karplus) в Гарварде в начале 70-х. Варшель имел подготовку в области меж- и внутримолекулярных потенциалов, Карплюс же имел обладал опытом квантово-химических расчетов. Вместе они создали программу, которая могла отлично вычислять π-электронные и колебательные спектры ряда плоских молекул [13]. В основе программы лежало классическое рассмотрение σ-электронов и ядер, а для π-электронов использовался скорректированный квантово-химический метод PPP (Praiser—Parr—Pople) [14]. На рис. 2 представлена типичная молекула, рассмотренная в работе [13].
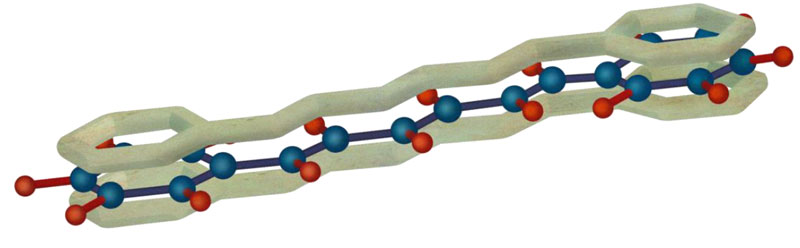
Рисунок 2. Зеркально симметричная молекула 1,6-дифенил-1,3,5-гексатриена, изученная Мартином Карплюсом и Ариэ Варшелем.
Эта работа стала первой, в которой было показано, что возможно создание гибридных методов, сочетающих в себе достоинства классических и квантовых методов в описании сложных химических систем. В данном случае рассмотрение было ограничено плоскими молекулами, в которых соображения симметрии позволяют естественным образом провести разделение между π-электронами, рассматриваемыми квантово-химически, и σ-электронами, рассматриваемыми классически, но позже было показано, что метод может быть применен не только к плоским молекулам. В своей работе «Диэлектрическая, электростатическая и стерическая стабилизация иона карбония в реакции с лизоцимом» [15] Карплюс и Варшель продемонстрировали, что существует общая схема разделения электронов на те, которые будут включены в классическую модель, и те, которые будут в явном виде описаны квантово-химически. Кроме того, были созданы схемы обмена энергией между классической и квантово-химической подсистемами, а также между ними обеими и диэлектрическим окружением. Общий вид рассмотренной системы представлен на рис. 3.
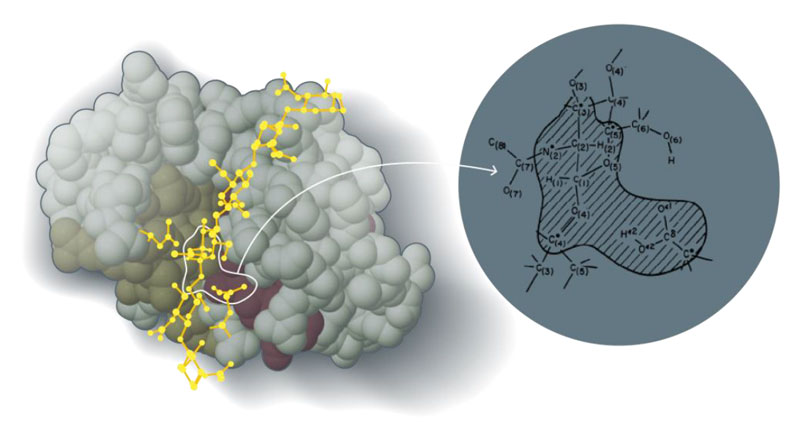
Рисунок 3. Чтобы понять, как лизоцим расщепляет гликозидную цепь, с помощью квантовой химии необходимо смоделировать только соответствующие части системы, в то время как остальная часть системы может быть рассмотрена с использованием молекулярной механики или как непрерывная среда
[15], рисунок адаптирован
Примерно в то же время был сделан еще один важный шаг, который позволил изучать еще бoльшие системы. В своей работе, посвященной фолдингу бычьего панкреатического ингибитора трипсина (bovine pancreas trypsin inhibitor, BPTI) [8], [16], Левитт и Варшель ввели псевдоатомы — частицы, объединяющие несколько атомов (рис. 4). Такой подход, называемый крупнозернистым представлением, позволяет ускорить расчеты, поскольку сокращает число частиц в системе и особенно число парных взаимодействий между ними.
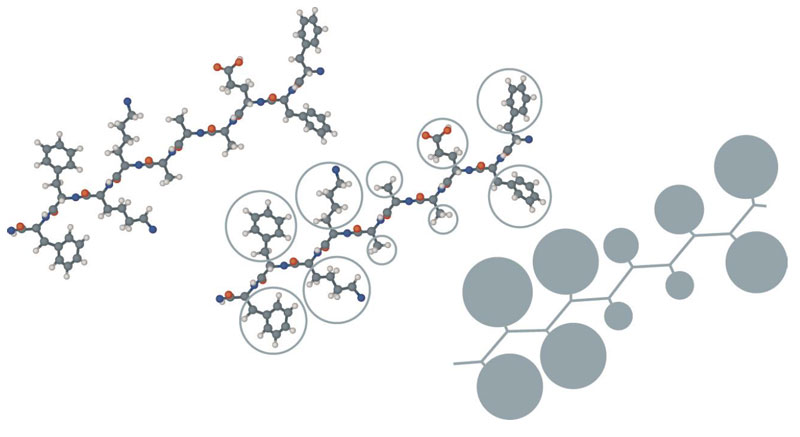
Рисунок 4. Рассмотрение точной структуры полипептидной цепи (сверху) может быть упрощено введением контактного объема для каждого аминокислотного остатка (в центре) и использованием получившегося «ожерелья» (снизу) для дальнейших расчетов.
Проблема фолдинга белка — то есть задача определения пространственной (третичной) структуры белка исходя из его аминокислотной последовательности — активно решается в настоящее время. Современные алгоритмы предсказания структуры позволяют решать эту задачу лишь для относительно небольших белков (менее 200 аминокислотных остатков), но этого совершенно недостаточно для удовлетворения потребностей структурной биологии [17].
Мультимасштабное моделирование сегодня
Работа, получившая в этом году признание Нобелевского комитета, стала отправной точкой как для дальнейшего теоретического анализа и создания более точных моделей, так и для прикладных исследований. Предложенные методы были применены к изучению не только сложных процессов в органической химии и биохимии, но и гетерогенного катализа и теоретического расчета спектров молекул, растворенных в жидкостях. Но важнее всего то, что эта работа положила начало плодотворному сотрудничеству между теоретиками и экспериментаторами, что позволило сделать решаемыми многие неприступные прежде задачи.
Как говорил русский математик и механик 19 века Пафнутий Львович Чебышёв: «Теория без практики мертва и бесплодна, практика без теории бесполезна и пагубна». В связи с этим очень символично, что один из суперкомпьютеров МГУ так и называется «Чебышев», а среди проводимых на нем расчетов большую долю занимают как раз квантово-химические и молекулярно-механические расчеты сложных биологических систем.
В СССР пионерские работы в области молекулярной динамики были сделаны в Вычислительном центре Академии наук в г. Пущино Н.К. Балабаевым [18]. В настоящее время в России в области молекулярного моделирования биологических структур работают несколько групп ученых. Это группа молекулярного моделирования под рук. проф. К.В. Шайтана на биологическом факультете МГУ, лаборатория моделирования биомолекулярных систем под рук. проф. Р.Г. Ефремова в Институте биоорганической химии РАН, лаборатория структурной биоинформатики под рук. д.б.н. А.В. Веселовского в Институте биомедицинской химии РАМН, лаборатория химической кибернетики под рук. проф. А.В. Немухина на химическом факультете МГУ, группа компьютерного молекулярного дизайна под рук. в.н.с. В.А. Палюлина на химическом факультете МГУ, лаборатория биокатализа и биотрансформаций под рук. проф. В.К. Швядаса НИИ ФХБ имени А.Н. Белозерского МГУ, группа под рук. с.н.с. А.Л. Рабиновича в лаборатории экологической биохимии Института биологии КарНЦ РАН.
Написано по пресс-релизу Нобелевского комитета.
Литература
- Ловля бабочек, или Чем структурная геномика поможет биологии;
- На заре молекулярной графики;
- F. H. Westheimer, Joseph E. Mayer. (1946). The Theory of the Racemization of Optically Active Derivatives of Diphenyl. The Journal of Chemical Physics. 14, 733-738;
- Terrell L. Hill. (1946). On Steric Effects. The Journal of Chemical Physics. 14, 465-465;
- I. Dostrovsky, E. D. Hughes, C. K. Ingold. (1946). 50. Mechanism of substitution at a saturated carbon atom. Part XXXII. The rôle of steric hindrance. (Section G) magnitude of steric effects, range of occurrence of steric and polar effects, and place of the wagner rearrangement in nucleophilic substitution and elimination. J. Chem. Soc.. 0, 173-194;
- Norman L. Allinger, Mary Ann Miller, Libby W. Chow, R. A. Ford, J. C. Graham. (1965). The Calculated Electronic Spectra and Structures of Some Cyclic Conjugated Hydrocarbons1,2. J. Am. Chem. Soc.. 87, 3430-3435;
- George Némethy, Harold A. Scheraga. (1965). Theoretical determination of sterically allowed conformations of a polypeptide chain by a computer method. Biopolymers. 3, 155-184;
- Молекулярная динамика биомолекул. Часть I. История полувековой давности;
- S. Lifson, A. Warshel. (1968). Consistent Force Field for Calculations of Conformations, Vibrational Spectra, and Enthalpies of Cycloalkane andn‐Alkane Molecules. The Journal of Chemical Physics. 49, 5116-5129;
- Michael Levitt, Shneior Lifson. (1969). Refinement of protein conformations using a macromolecular energy minimization procedure. Journal of Molecular Biology. 46, 269-279;
- Frenkel D. and Smit B. Understanding Molecular Simulations. San Diego (USA): Academic Press, 1996;
- R. Car, M. Parrinello. (1985). Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett.. 55, 2471-2474;
- A. Warshel, M. Karplus. (1972). Calculation of ground and excited state potential surfaces of conjugated molecules. I. Formulation and parametrization. J. Am. Chem. Soc.. 94, 5612-5625;
- Rudolph Pariser, Robert G. Parr. (1953). A Semi‐Empirical Theory of the Electronic Spectra and Electronic Structure of Complex Unsaturated Molecules. I.. The Journal of Chemical Physics. 21, 466-471;
- A. Warshel, M. Levitt. (1976). Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. Journal of Molecular Biology. 103, 227-249;
- Michael Levitt, Arieh Warshel. (1975). Computer simulation of protein folding. Nature. 253, 694-698;
- Торжество компьютерных методов: предсказание строения белков;
- Yu. Ya. Gotlib, N. K. Balabaev, A. A. Darinskii, I. M. Neelov. (1980). Investigation of Local Motions in Polymers by the Method of Molecular Dynamics. Macromolecules. 13, 602-608.