Молекулярная коммутация — новый механизм регуляции генов и не только
02 апреля 2024
Молекулярная коммутация — новый механизм регуляции генов и не только
- 1905
- 0
- 8
Рисунок в полном размере.
иллюстрация сгенерирована при помощи Microsoft designer
-
Автор
-
Редакторы
Статья на конкурс «Био/Мол/Текст»: Все мы давно привыкли к структуре ДНК. В этой изящной молекуле при помощи одной цепи можно однозначно восстановить вторую. Это свойство не только обеспечивает стабильность и прочность ДНК, но и делает возможными такие процессы, как репликация и транскрипция. По сути, открытие структуры ДНК положило начало современной молекулярной биологии. Однако, несмотря на всю красоту двойной спирали, нуклеотиды могут взаимодействовать и без ее образования. И нет, речь идет не про образование вторичной структуры РНК или ДНК. В новом исследовании изучалось именно взаимодействие между двумя цепями нуклеотидов как в ДНК, лишь с более короткими молекулами длинной в несколько десятков пар нуклеотидов. Только, в отличие от ДНК, связь между цепочками была не стопроцентной, то есть не все нуклеотиды подходили друг к другу.
Конкурс «Био/Мол/Текст»-2023/2024
 Эта работа заняла первое место в номинации «Школьная» конкурса «Био/Мол/Текст»-2023/2024.
Эта работа заняла первое место в номинации «Школьная» конкурса «Био/Мол/Текст»-2023/2024.

Генеральный партнер конкурса — международная инновационная биотехнологическая компания BIOCAD.

«Книжный» спонсор конкурса — «Альпина нон-фикшн»
Континуум аффинностей
Не надо пугаться этого страшного термина, на самом деле все достаточно просто. Основная мысль в том, что, поскольку мы больше не обязаны идеально подстраивать друг под друга две цепи в молекуле, мы можем выбрать любое количество комплементарных (образующих пары) нуклеотидов. При этом чем больше их будет, тем сильнее связь между двумя цепями. Это значит, что можно подобрать две цепочки ДНК с практически любой силой связи или стабильностью. Дальше идет чуть более строгое определение, но если вы знаете, что такое константа диссоциации, его можно понять без труда.
На всякий случай поясню, как считается константа диссоциации. Константа диссоциации Kd[AB] определяет стабильность комплекса AB — чем она выше, тем меньше концентрация комплекса AB и тем больше концентрация A и B по отдельности. Формула, по которой считается константа диссоциации: [A][B]/[AB], где [A] — концентрация свободного A, [B] — концентрация свободного B, а [AB] — концентрация комплекса, везде она измеряется в моль/литр. В контексте этой статьи константа диссоциации показывает стабильность комплекса из двух одноцепочечных ДНК.
Дальше мы будем в основном оперировать именно одноцепочечными ДНК так как Kd между двумя половинками может быть достаточно высоким, чтобы они практически не соединялись; к тому же в системе может быть больше, чем 2 цепочки ДНК. Благодаря связи произвольного числа комплементарных нуклеотидов разные пары одноцепочечных ДНК (или «половинок» нормальной двухцепочечной молекулы ДНК) могут иметь огромный набор различных Kd, автор исследования назвал это свойство континуумом аффинностей (см. риc. 1). Причем континуум аффинностей даже у коротких молекул очень «плотный», то есть для любой молекулы можно подобрать пару с практически любой аффинностью. Более того, можно подобрать такой набор одноцепочечных ДНК, чтобы у каждой возможной пары была определенная константа диссоциации.
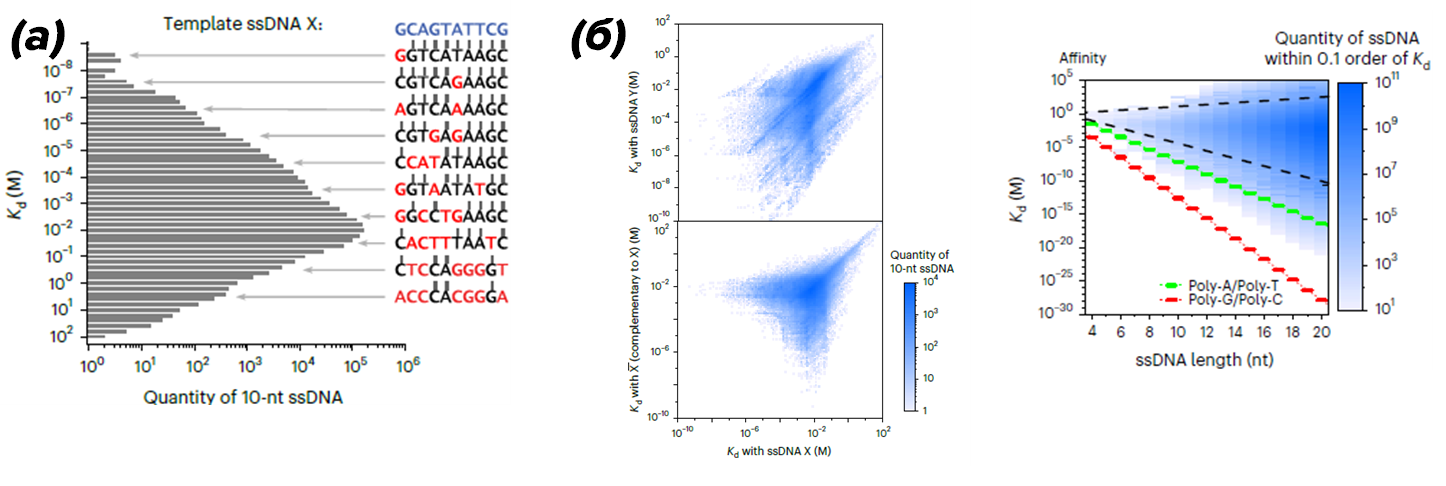
Рисунок 1. Одномерный (а) и двумерный (б) континуум аффинности — количество цепочек ДНК, имеющих определенное сродство (аффинность) к одной и более определенными цепями ДНК. Хотя «плотность» графика может особо не впечатлять, стоит заметить, что рассматриваются олигонуклеотиды длиной всего в 10 нуклеотидов. У более длинных молекул континуум аффинностей будет намного более обширным. На графике (а) показано количество цепочек ДНК, имеющих определенное сродство к цепочке X, которая выбрана случайно. На графиках (б) оттенками синего обозначено количество возможных цепей ДНК с разным сродством к цепочке X и цепочке Y или X, где X — это случайная цепочка ДНК длиной 10 нуклеотидов, X — цепь, комплементарная X, а Y — другая случайная цепь ДНК той же длины.
Снизу показан разброс аффинности для оцДНК (одноцепочечной ДНК) различной длины, оттенками синего показаны количества оцДНК с определенной аффинности к случайной оцДНК определенной длины. Зеленая линия — аффинность комплекса из 2 цепей — одна содержит только аденин, вторая — только тимин. Красная линия показывает то же, но для гуанина и цитозина.
Например, если в системе из олигов A, B и C Kd [AB] меньше, чем Kd [AC], то комплексы AB будут выгоднее, чем комплексы AC, и комплексов AB будет больше. При этом можно подобрать такие С и B, чтобы они, например, взаимодействовали только с A, но не друг с другом — Kd комплекса CB должна быть очень высокой.
На этом этапе стоит сделать еще одно небольшое пояснение: хотя выше речь шла о «похожих на ДНК» молекулах: на самом деле, с РНК все работает точно так же — двухцепочечные РНК тоже могут иметь различную «прочность» или, если по-научному — различную Kd между отдельными цепями. Короткие одноцепочечные ДНК или РНК называются олигонуклеотидами или олигами. Дальше этот термин будет использоваться достаточно много.
Дальше начинается самое интересное. Системы, где одни олиги могут вытеснять другие из комплексов, могут быть намного сложнее, чем кажется на первый взгляд. Из олигов можно даже создавать системы, которые ведут себя как схемы в электронике! Но обо всем по порядку.
Но сначала стоит обсудить обсудить общие «правила», по которым проводился эксперимент, ведь невозможно просто взять и посмотреть, какие олиги с какими соединяются. Во всех экспериментах в исследовании использовались 3 основных «типа» олигонуклеотидов: I (input — «входные данные»), Q (quencher — «тушитель») и S (signal — сигнал). Цепь S способна испускать световой сигнал благодаря прикрепленному к 5’ концу флуоресцентному красителю Cy5, но цепь Q блокирует этот сигнал при помощи тушителя BHQ2 на ее 3’ конце который поглощает излучение Cy5, когда цепь Q соединяется с S. Цепь I, в свою очередь, добавляется в систему и неким образом влияет на нее. В такой системе мы можем фиксировать флуоресценцию Cy5, только когда цепь S свободна, т.е. не связана с тушителем.
Начнем с самой простой системы олигов, которая к тому же уже рассматривалась выше. Для того, чтобы S высвобождалась при добавлении I, достаточно только трех вышеупомянутых молекул — S, I и Q. Это можно реализовать, если подобрать такой I, чтобы он лучше соединялся с Q, чем S и вытеснял S из менее выгодного комплекса с Q. При этом I не должна взаимодействовать с S (рис. 2).
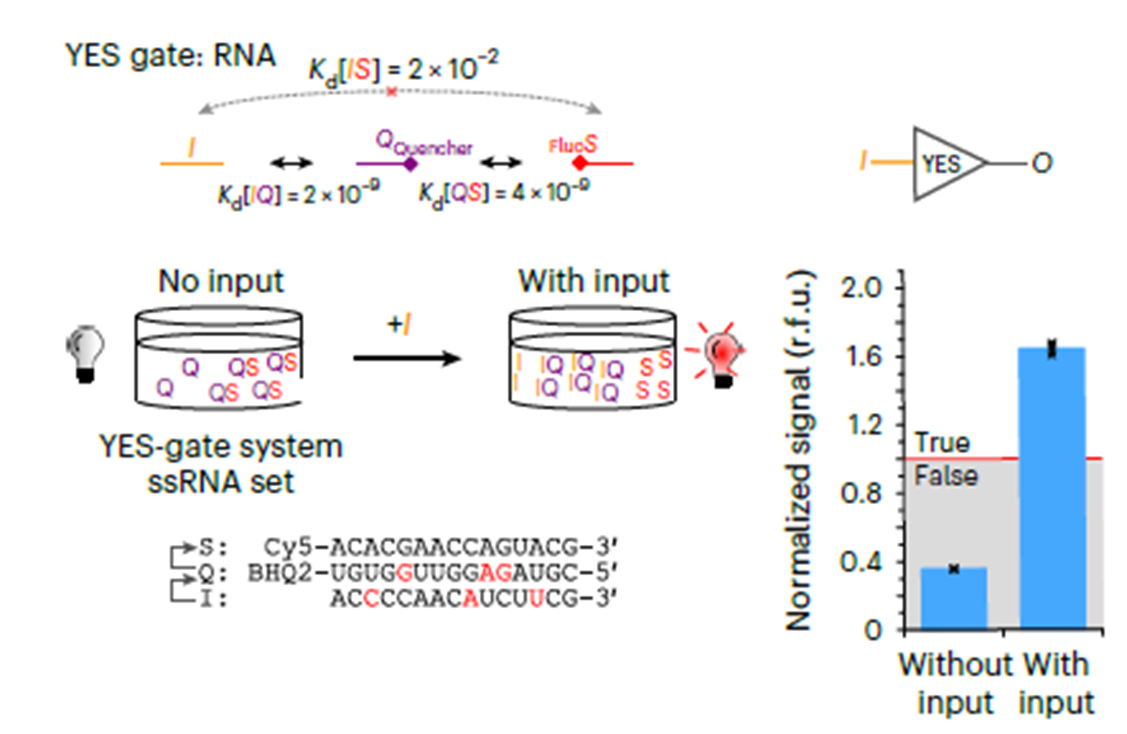
Рисунок 2. Принцип работы оператора ДА. Т.к. Kd[QS] достаточна низка (4*10-9), Q будет связываться с S. Однако Kd[IQ] < Kd[QS] (2*10-9 против 4*10-9), следовательно, комплекс IQ является более выгодным и будет образовываться чаще. При этом значение Kd[IS] очень велико, поэтому комплексы IS почти не будут образовываться. В правом верхнем углу показана система в упрощенном виде. В правом нижним углу находится иллюстрация силы сигнала с добавлением I и без его добавления.
Если же мы хотим, чтобы добавление I, наоборот, блокировало сигнал (рис. 3), в систему достаточно добавить только один олиг M, который без добавления I связывается с Q (как I из прошлого примера), и сигнал испускается. Однако при добавлении I он забирает M из комплекса с Q, Q высвобождается и связывается с S, блокируя тем самым сигнал. Здесь, как и в предыдущей системе, цепи ДНК образуют только такие пары.
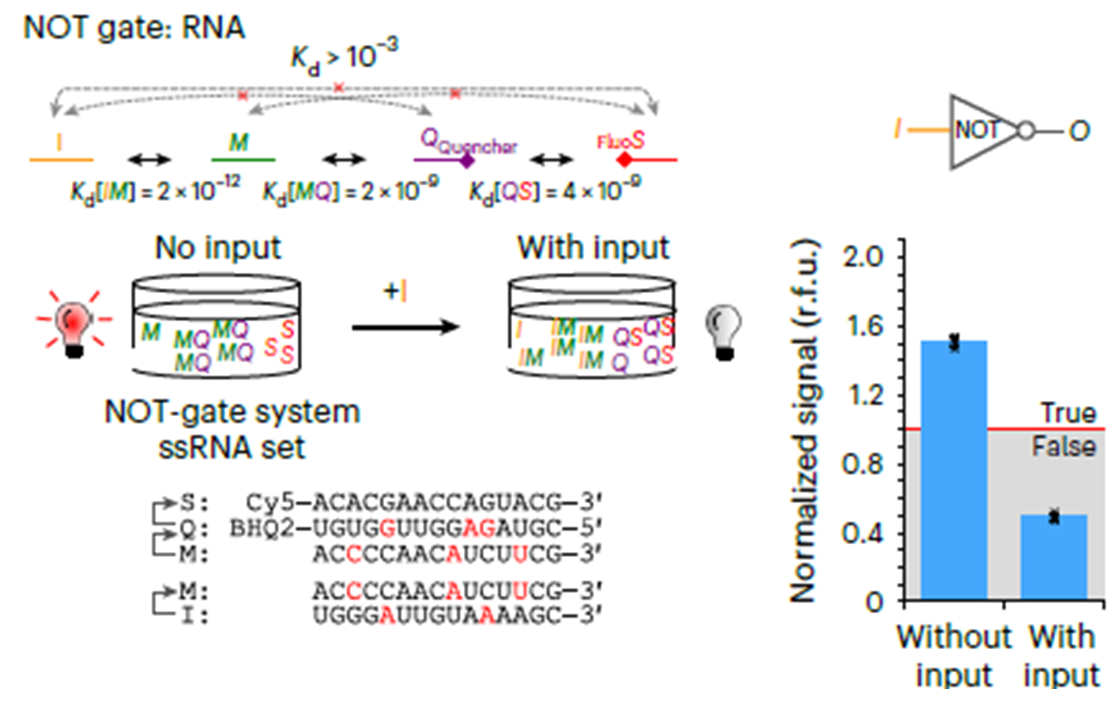
Рисунок 3. Логическая операция отрицания. На рисунке слева сверху показана схема взаимодействия олигонуклеотидов и константы диссоциации их комплексов. Ниже показана визуализация работы логической операции и последовательности РНК, которые были использованы. Справа показаны обозначение операции отрицания и результаты измерения сигнала при добавлении I и без его добавления.
У вас может возникнуть вопрос: в чем практический смысл всего, что описывалось выше? В генной инженерии есть метод подавления (сайленсинга) генов при помощи связывания мРНК с комплементарной ей одноцепочечной ДНК (далее M1) и разрезания этой мРНК РНКазой-H (которая разрезает РНК в комплексе РНК-ДНК) [1]. Этот метод также используется при лечении генетических и вирусных заболеваний. В исследовании [2] моделируется ситуация, где этот метод «ломается», и мРНК остается целой. При этом такой эффект оказывает только один олиг, который даже не комплементарен мРНК или M1. По сути, автор сконструировал систему как ту, что рассматривалась выше в первом примере (рис. 2). Автор исследования провел эксперимент: в нем в качестве сигнальной РНК (S) использовалась РНК, кодирующая белок люциферазу (люцифераза отвечает за биолюминесценцию), а одноцепочечную ДНК M1 — как тушитель. Далее автор подобрал максимально некомплементарную по отношению к S РНК R1 (ее можно рассматривать как аналог цепи I из вышеописанной системы) и такую РНК M2, чтобы она выполняла роль M из второго примера (рис. 3). В итоге получилась система, где сайленсинг мРНК происходит только при добавлении R1. При отсутствии R1 сигнал наблюдается, однако при ее добавлении трансляция люциферазы блокируется, и сигнал не наблюдается. Этот эксперимент демонстрирует, что некомплементарные к мРНК и M1 олиги могут влиять на этот механизм и даже подавлять его работу, хотя обычно при поиске возможных побочных эффектов рассматриваются только комплементарные взаимодействия.
В свою очередь, уже ДНК и РНК, используемые в генной терапии, могут влиять на естественные процессы в клетке схожим образом, что может быть причиной некоторых побочных эффектов генной терапии.
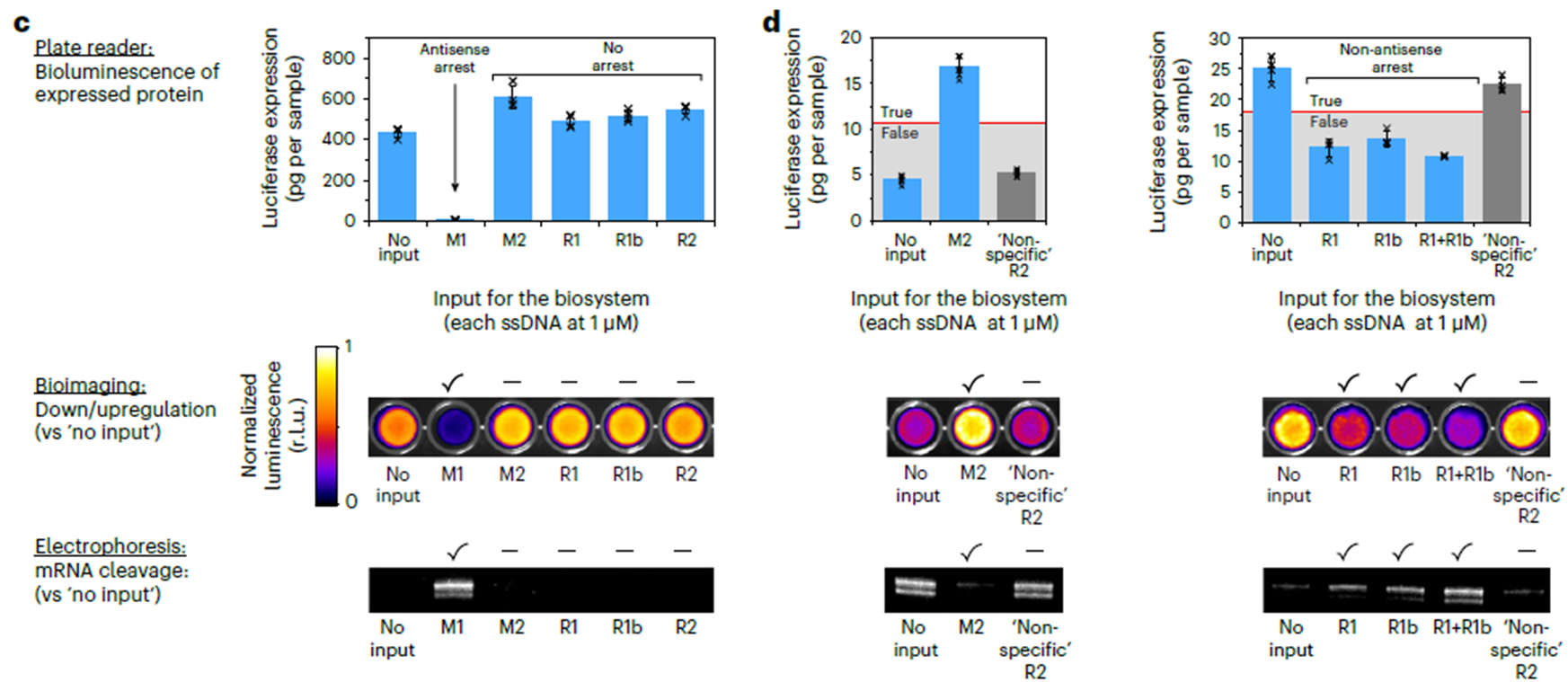
Рисунок 4. Экспрессия люциферазы при добавлении различных наборов олигонуклеотидов. Слева находится схема экспрессии при наличии в системе только иРНК люциферазы, РНКазы-H и системы трансляции; она показывает, что никакие олиги, кроме M1, не влияют на иРНК. Вторая схема показывает результаты измерения концентрации люциферазы в той же системе, но с добавлением M1. Третья схема показывает функционирование полной системы из иРНК, M1 и M2 и РНКазы-H. В данном случае R1, R1b и R2 — максимально некомплементарные к иРНК короткие молекулы РНК, при этом R1 и R1b способны связываться с M2 и тем самым блокировать трансляцию. Все измерения соответствуют модели.
Краткое введение в Булеву алгебру
Вернемся к теории. Я упоминал, что системы из олигонуклеотидов могут быть похожи на схемы в электронике, поэтому, чтобы лучше понять системы из олигонуклеотидов, сначала нужно осознать принцип работы вычислительных схем в электронике. Поэтому, мне придется сделать небольшое отступление в математику. Булева алгебра — это раздел математики, который работает с логическими значениями (далее: 1 — наличие сигнала, 0 — отсутствие сигнала). В ней существует 4 «основные» операции или 4 базовых логических вентиля: ДА, НЕТ, И, ИЛИ. Операция ДА принимает на вход аргумент x, а на выход выводит то его значение (0, если x = 0; и 1, если x = 1). Операция НЕТ на вход тоже принимает одну переменную и выводит противоположное значение (если x = 1, то 0; если x = 0, то 1). Операции И и ИЛИ принимают на вход по 2 или больше переменных. Операция И возвращает ответ 1, если все входные переменные равны 1. Операция ИЛИ выводит 1, если хотя бы одна из входных переменных равна 1. В противном случае обе операции возвращают 0. При помощи комбинирования логических вентилей можно создавать Булевы функции, которые определенным образом обрабатывают набор логических значений или двоичный код и которые можно реализовывать в виде электронных схем.
Математика на олигах
Первые два — логические вентили ДА и НЕТ — мы уже обсудили (см. рис. 2 и рис. 3). Остаются еще два — вентили И и ИЛИ. Для реализации операции И используется 2 цепи I: I1 и I2. В системе также присутствуют 2 Q: Q1 и Q2. Каждый Q соединяется с S и блокирует ее. При этом концентрация каждого Q достаточна для блокирования всего S. При этом Q1 и Q2 связываются с I1 и I2, и эта связь сильнее, чем связь с S, поэтому когда все Q связаны, S высвобождается и испускает сигнал. При этом каждая I связывается только со своим Q и больше ни с какими другими цепями. Q тоже не взаимодействуют друг с другом. В реализации операции ИЛИ, в свою очередь, участвует только одна Q, с которой связываются все три I. На самом деле, обе операции могут принимать большее количество I, в таком случае количество Q тоже будет другим, равным количеству I. Максимальное количество I, при котором операция И будет работать, если использовать олиги длиной 15 нуклеотидов, равно 572. По крайней мере, такой результат показывает алгоритм NUPACK, который применялся в исследовании для моделирования взаимодействия НК (рис. 5).
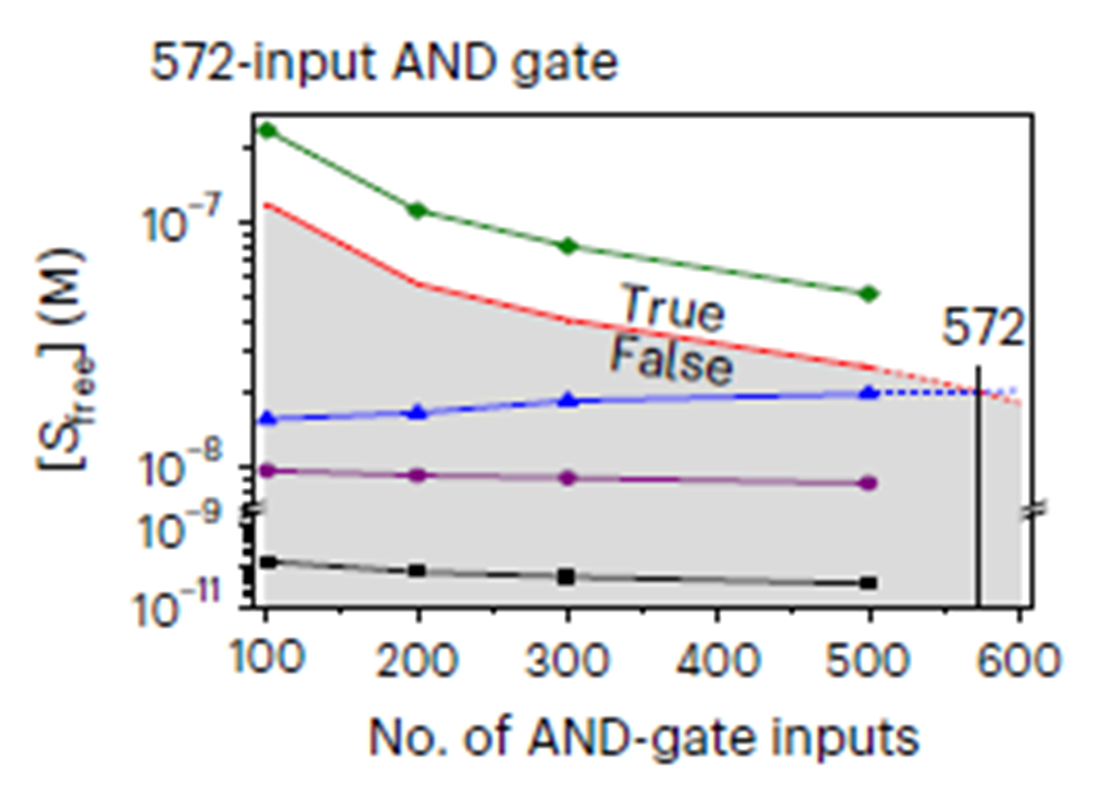
Рисунок 5. Показана зависимость концентрации S при различных входных данных от количества входов для операции И. Зеленые ромбы — на вход даются все I; черные квадраты — на вход не подавалось ничего. Синие треугольники — максимальное значение при добавлении в систему всех I кроме одного, фиолетовые круги — минимальное значение при тех же условиях.
Теперь у нас есть все, чтобы собирать «электронные схемы» при помощи олигонуклеотидов. В данном случае вместо цепочки S, которая сама может испускать сигнал, можно использовать другую цепь, которая при высвобождении будет участвовать в последующих операциях. В исследовании [2] в качестве примера такой схемы демонстрируется система, которая может считать квадратный корень 4-битного числа. Система принимает 4 I — каждый ответственен за свой разряд, если она дана, в нем стоит 1, иначе — 0. Ответ выводится по 2 каналам — S1 и S2. Стоит заметить, что корень вычисляется с точностью до целых с округлением вниз (рис. 6).
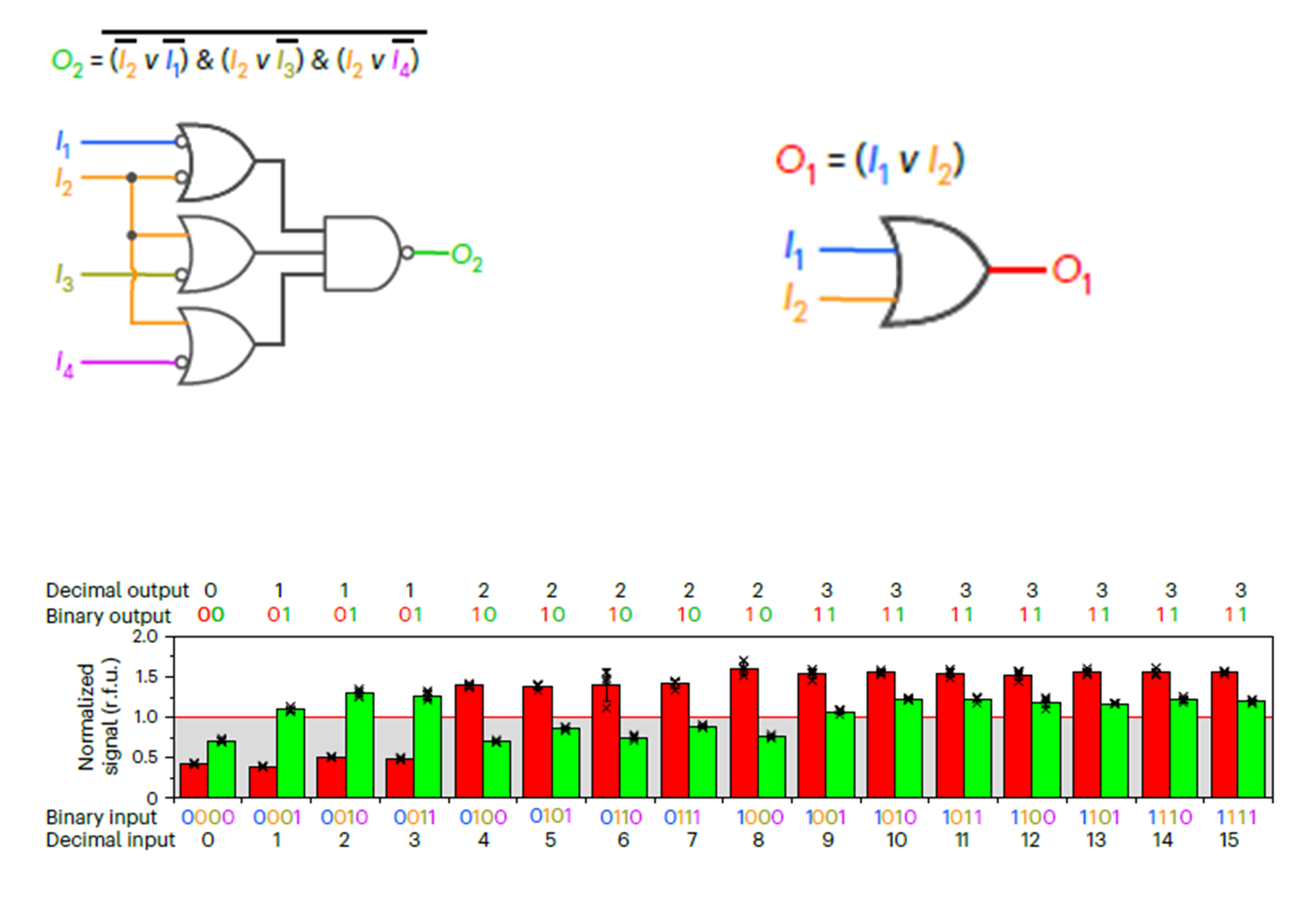
Рисунок 6. На данной схеме символ полукруга с заостренным краем обозначает вентиль ИЛИ, символ полуэллипса обозначает вентиль И, а маленькие кружочки — вентиль НЕ. O1 и O2 обозначают высвобождение S1 и S2, соответственно. Ниже показаны результаты измерения сигнала по каждому каналу O1 (зеленый) и O2 (красный) при добавлении различных комбинаций I. Красная линия обозначает порог значения при котором оно будет приниматься за ДА.
Данная схема работает крайне просто. Корень числа будет иметь единицу во 2 разряде, и канал O1 будет передавать сигнал (минимальное такое число — 10 в двоичной системе счисления, 2 — в десятичной), только если это число больше или равно 4 (0100 в двоичной системе счисления), т.е. в 3 разряде или выше стоит 1 (канал I1 или канал I2 равен 1). Схема для O2 более сложная, но принцип работы тот же — она возвращает положительный ответ только для определенного набора чисел. При этом данная система решает задачу вычисления квадратного корня 15-битного числа намного быстрее аналогов. На данный момент самое быстрое решение требует 37 олигов и 25 минут [3], в то время как механизм, основанный на молекулярной коммутации, считает ответ за 5 минут.
Хранение информации
Реализация Булевых функций — это не все, на что способны системы из олигов. При помощи вышеописанных логических вентилей автор исследования [2] создает простую систему хранения информации с функциями записи и чтения. Она состоит из трех вентилей И и четырех допустимых I: I1, I2, I3, а также R. Активация каждого из вентилей ведет к высвобождению своего S (каждый S имеет свою частоту флуоресценции). Каждый из трех вентилей И активируется одним из I и R, т.е. без R сигнал испускаться вообще не будет. Для записи информации в эту систему нужно добавить определенный набор I, а для его чтения нужно добавить R. Такую «флешку» невозможно прочитать, не имея олига R. Возможно, эта технология может быть использована для более надежного хранения данных.
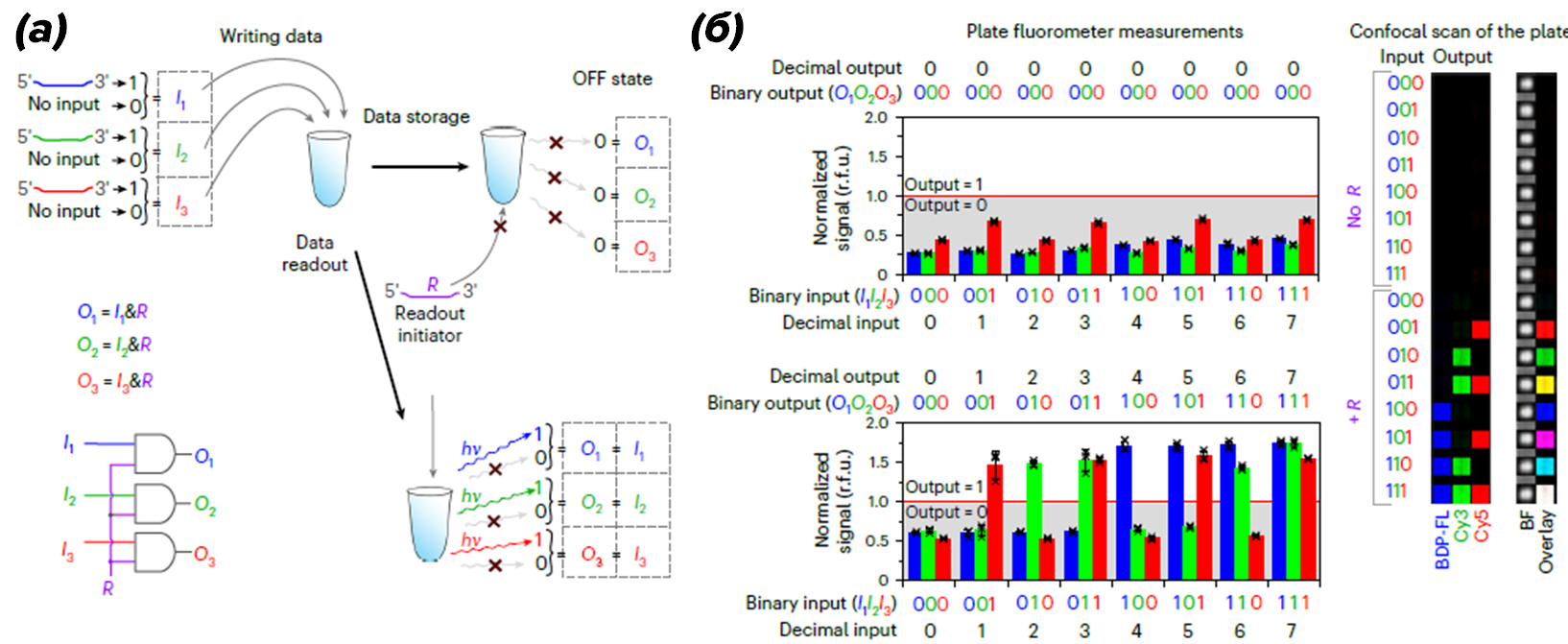
Рисунок 7. В левом нижнем углу показана схема данной системы (O1, O2, O3 обозначают высвобождение соответствующего S). Оставшуюся часть схемы (a) заполняет иллюстрация работы системы. Сверху — без добавления R (сигнала нет), снизу — с добавлением R (сигнал для каждого S зависит от наличия соответствующего I). Справа показаны результаты наблюдения для этой системы при добавлении различных комбинаций I и R.
Аналоговые функции
Автор приводит и другой, «аналоговый» механизм вычисления при помощи молекул одноцепочечной ДНК (рис. 6). Этот механизм не имеет ничего общего с булевыми функциями и вообще с тем, что описывалось выше вплоть до введения континуума аффинностей. Здесь всего одна цепь ДНК подается на вход, далее «ответ» определяется концентрацией свободной S. В данном случае набор молекул одноцепочечных ДНК подбирался при помощи эволюционного алгоритма. Принцип работы эволюционного алгоритма заключается в том, что сначала генерируется случайный набор ДНК, потом создаются «вариаций» этого набора, т.е. в последовательности ДНК вносятся мутации. Далее специальная программа моделирует систему из этих ДНК для каждой вариации и отбирается вариант, при котором ответ является наиболее точным. После этого отобранный вариант снова подвергается мутациям и снова отбирается самый успешный вариант. Так повторяется, пока погрешность ответа не достигнет определенного значения. Если же такого набора ДНК не удается достигнуть после некоторого количества итераций, в систему добавляется новая цепь ДНК.
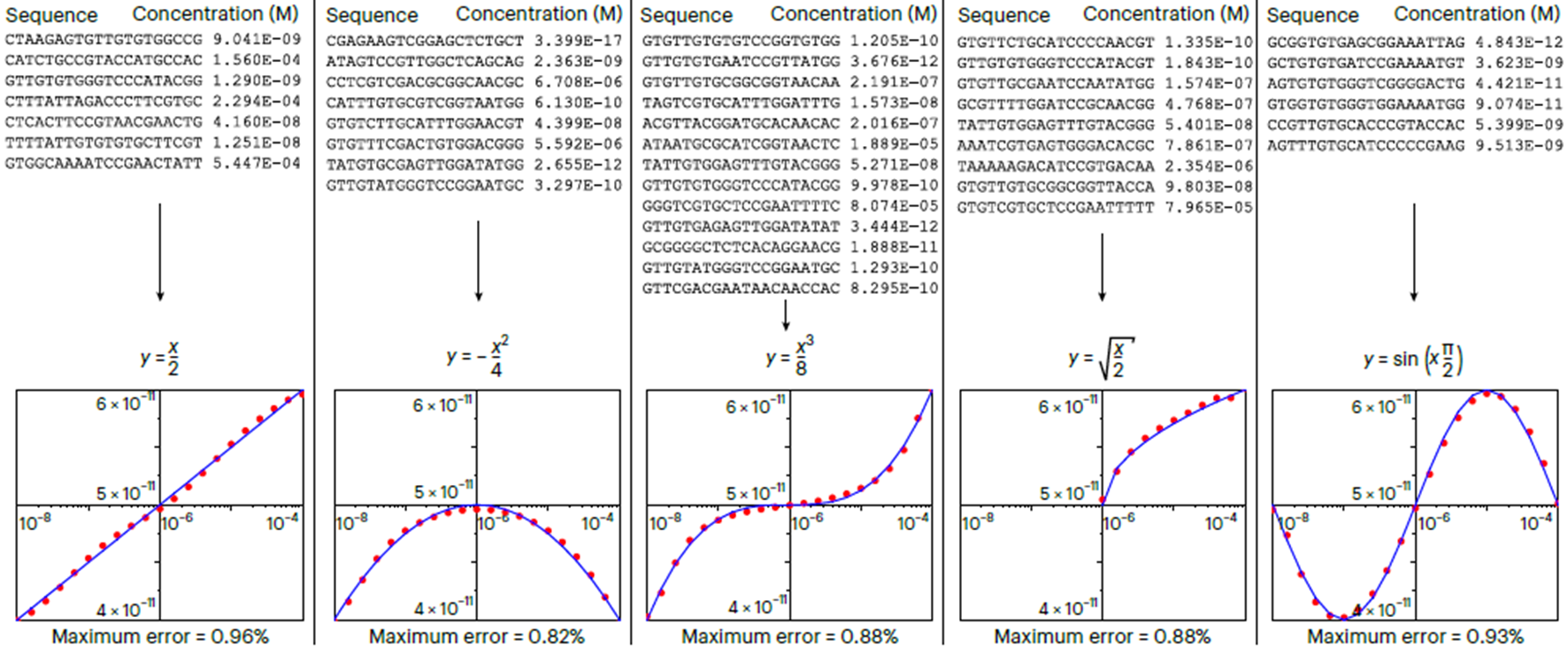
Рисунок 8. Наборы последовательностей одноцепочечной ДНК и их концентраций для реализации некоторых из функций. Ниже на график функции (синяя линия) наложены результаты измерения концентрации y при заданном x (красные точки).
Значение и применение
Работают ли олиги в живых клетках так же, как в искусственных системах? Этот вопрос остается открытым. Несмотря на все эксперименты, которые проводились в исследовании [2], роль молекулярной коммутации в экспрессии генов остается спорной: возможно, что клетка постоянно борется с короткими НК и минимизирует их влияние на трансляцию. Однако если такой механизм и правда работает в клетках, он может иметь огромное значение для биологии и медицины. Например, молекулярная коммутация могла бы позволять клеткам осуществлять регуляцию генов с очень большой точностью благодаря схемам, описанным выше. Факт того, что даже наименее комплементарные олигонуклеотиды могут влиять на работу гена, может быть причиной побочных эффектов генной терапии. Автор исследования предполагает, что этот феномен может играть роль в формировании кратковременной памяти т.к. он не требует создания «дорогих» ковалентных связей. Он также рассуждает о том, что накопление низкоаффинных взаимодействий может влиять на старение и даже приводить к образованию рака.
Эффект молекулярной коммутации, помимо всего прочего, может в теории использоваться для хранения информации и создании более совершенного ДНК/РНК-компьютера. Кроме того, эффект молекулярной коммутации применим не только к ДНК или РНК (собственно, поэтому эффект назван именно молекулярной коммутацией, а не, например, ДНК-коммутацией или РНК-коммутацией). Белки, например, белковые рецепторы, сигнальные белки и белки-переносчики, тоже могут подчиняться этому принципу.
В любом случае, открытие порождает больше вопросов, чем дает ответов, так что тема взаимодействия олигов с низкой взаимной аффинностью открыта для новых исследований.
Литература
- C. Frank Bennett, Eric E. Swayze. (2010). RNA Targeting Therapeutics: Molecular Mechanisms of Antisense Oligonucleotides as a Therapeutic Platform. Annu. Rev. Pharmacol. Toxicol.. 50, 259-293;
- Maxim P. Nikitin. (2023). Non-complementary strand commutation as a fundamental alternative for information processing by DNA and gene regulation. Nat. Chem.. 15, 70-82;
- Tianqi Song, Abeer Eshra, Shalin Shah, Hieu Bui, Daniel Fu, et. al.. (2019). Fast and compact DNA logic circuits based on single-stranded gates using strand-displacing polymerase. Nat. Nanotechnol.. 14, 1075-1081.