Голуби умеют считать наравне с приматами
29 декабря 2011
Голуби умеют считать наравне с приматами
- 2902
- 5
- 1
Кому бы могло прийти в голову, что голуби способны не просто считать, но постичь начала абстрактной арифметики!
-
Автор
-
Редакторы
Темы
Издавна принято думать, что способность к счету, а особенно к абстрактному восприятию чисел, является уникальной чертой людей, неразрывно связанной с языком и культурой. Однако ученые давно уже предполагают, что способность эта строится на эволюционно древнем механизме «примерного счета», что и подтверждается в экспериментах: многие животные — от пчел до приматов — различают численность предметов. Не так давно показано, что шимпанзе обладают также зачатками абстрактного арифметического мышления. Но никто не думал, что, оказывается, по этой способности обезьянам не уступают... голуби!
В своей знаковой работе американские этологи Бреннон (E.M. Brannon) и Терэйс (H.S. Terrace) показали, что макаки резус могут не только различать численность предметов, но и обладают зачатками абстрактного арифметического мышления. «Обучившись» счету на примере групп из одного, двух, трех или четырех предметов, обезьяны затем уверенно оперировали числами в диапазоне от 1 до 9 [1]. При средней точности выполнения заданий >80% (рис. 1б), макаки работали тем точнее, чем больше была разница между числами, которые им приходилось сравнивать (рис. 1в), и, чем больше была эта разница, тем быстрее животные принимали решение (рис. 1г).
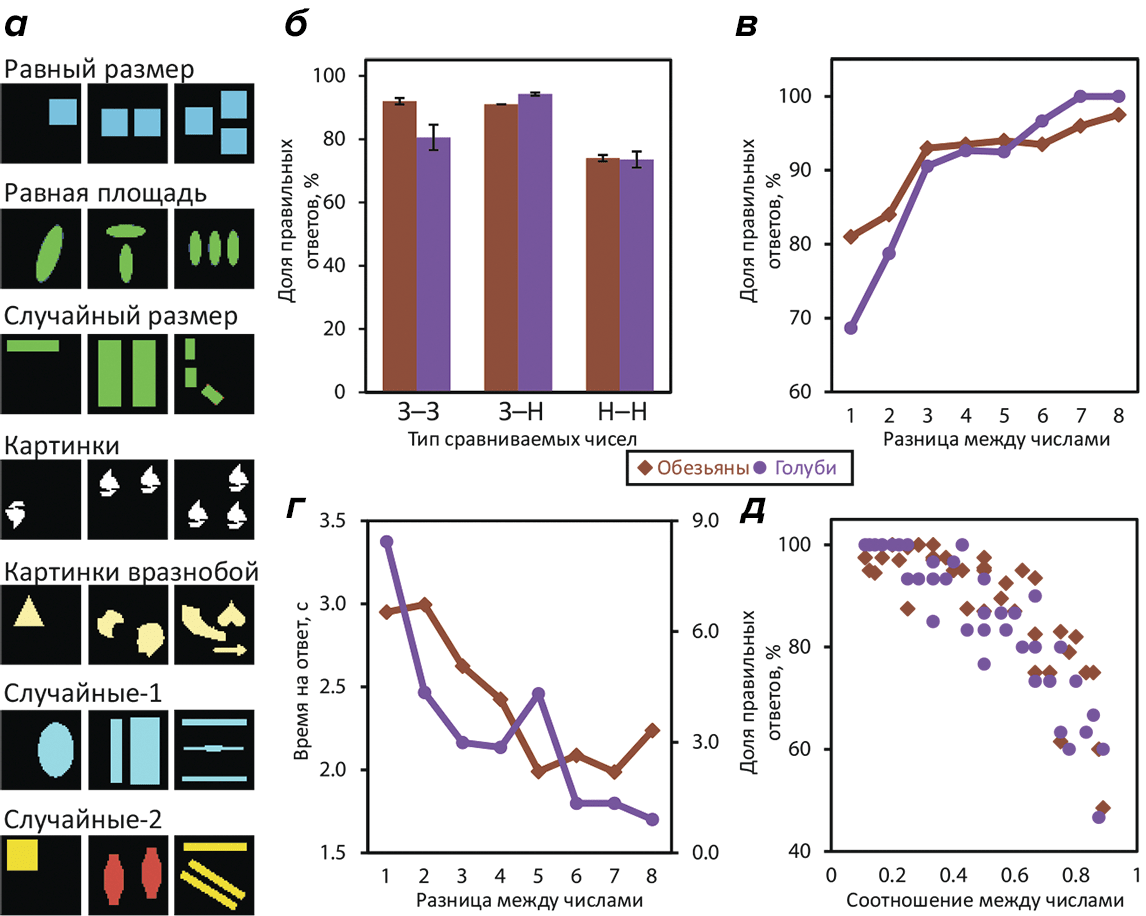
Рисунок 1. В устном счете голуби не уступают обезьянам! а — Карточки, использовавшиеся для «обучения» птиц. «Экзамен» принимали по более сложным карточкам, где число объектов достигало девяти. б — «Успеваемость» обезьян и голубей в сравнении двух чисел: «знакомых» между собой (З—З), «знакомых» с «незнакомым» (З—Н) и двух «незнакомых» (Н—Н). в — Точность ответов в зависимости от разницы между числами. г — Время, затрачиваемое на ответ, в зависимости от той же разницы. д — Точность ответов в зависимости от соотношения сравниваемых чисел (а не от разницы).
Интуитивно это объясняется достаточно просто: разницу тем легче заметить, чем она больше. На этот счет еще 1860 году был сформулирован основной психофизический закон — закон Вебера—Фехнера, согласно которому интенсивность ощущения пропорциональна логарифму интенсивности стимула. (Например, нам кажется одинаковой прибавка в яркости между двухламповой/четырехламповой и четырехламповой/восьмиламповой люстрами, в то время как физическая величина яркости во втором случае возрастает намного сильнее.) Обезьяны Бреннон и Терейса, в соответствии с этим законом, работали тем точнее, чем сильнее соотношение сравниваемых элементов отличалось от единицы (рис. 1д).
Под новый год в журнале Science появилась статья, в которой новозеландские исследователи поведения животных провели схожие опыты на голубях, чтобы определить, только ли приматы в состоянии постичь математические премудрости [2]? «Обучение» голубей проводили индивидуально; в качестве учебного пособия использовались 35 наборов из трех карточек — от одного до трех изображений на каждой (рис. 1а); изображения могли отличаться по форме, размеру и цвету. Чтобы исключить возможность того, что птицы не сравнивают карточки по числу изображений, а запоминают их как-то еще, в процессе обучения их «натаскали» правильно упорядочивать наборы независимо ни от чего, кроме числа изображений на них. Занятия длились сто дней.
Чтобы сдать «экзамен», птицам приходилось работать с материалами, по которым их не учили — количество изображений на карточках варьировало от 1 до 9. Правильные ответы подсчитывали отдельно для случаев, когда птицам приходилось сравнивать:
- Знакомые (З) карточки между собой — как на занятиях (З—З).
- Знакомые с незнакомыми (З—Н; на которых число изображений было 4–9).
- Незнакомые между собой (Н—Н).
Результаты этого эксперимента показали, что птицы, даже когда в ход пошли карточки, которые им не показывали на уроках, неплохо справляются с заданием (рис. 1б), а значит, обладают абстрактным понятием численности. Как и в случае обезьян, точность ответов повышалась, если разница между сравниваемыми числами была большой (рис. 1в), а время выбора, соответственно, снижалось (рис. 1г). Ну и наконец, закон Вебера—Фехнера сработал и тут: чем сильнее соотношение сравниваемых чисел отличалось от единицы, тем безошибочнее было решение задачи (рис. 1д).
Оказалось, что голуби в среднем ничуть не хуже обезьян справляются со счетом, когда в ход должно идти абстрактное мышление. (Уже известно, что голуби умеют считать [3], но раньше их способность к обобщению и решению задач с новыми объектами не изучали.)
Как всегда в таких случаях, предлагается два возможных механизма возникновения способности к «абстрактному» счету у птиц и приматов:
- Это могло быть у обеих групп животных независимо (конвергентно).
- Это древняя («примитивная») черта, присутствовавшая еще у общих предков птиц и млекопитающих.
Как бы то ни было, в последние десятилетия птицы «отвоевывают» способности, которых люди огульно их лишили, приписав только себе либо, на худой конец, приматам. Например, птицы обладают эпизодической памятью [4] и способностью использовать примитивные «орудия труда» [5].
Обнаружение способности абстрактно мыслить у птиц отсылает исследователей эволюционной психологии «вниз» по филогенетическому древу в поисках истоков Независимой мысли. :-) С Новым годом!
По материалам оригинальной статьи [2].
Литература
- E. M. Brannon. (1998). Ordering of the Numerosities 1 to 9 by Monkeys. Science. 282, 746-749;
- D. Scarf, H. Hayne, M. Colombo. (2011). Pigeons on Par with Primates in Numerical Competence. Science. 334, 1664-1664;
- William A. Roberts. (2010). “Counting” serially presented stimuli by human and nonhuman primates and pigeons. Learning and Motivation. 41, 241-251;
- Nicola S. Clayton, Anthony Dickinson. (1998). Episodic-like memory during cache recovery by scrub jays. Nature. 395, 272-274;
- C. Rutz, L. A. Bluff, N. Reed, J. Troscianko, J. Newton, et. al.. (2010). The Ecological Significance of Tool Use in New Caledonian Crows. Science. 329, 1523-1526.