Молекулярная динамика биомолекул. Часть I. История полувековой давности
02 августа 2007
Молекулярная динамика биомолекул. Часть I. История полувековой давности
- 10202
- 2
- 14
Фрагмент молекулы ДНК в ячейке с водой. 3D-изображение построено на основании данных расчетов МД.
-
Автор
-
Редакторы
В 2007 году у всех, кто занимается или просто интересуется компьютерным моделированием биомолекул, есть повод отметить два скромных юбилея — 50 лет первому опубликованному компьютерному расчету молекулярной динамики и 30 лет первому расчету динамики белковой глобулы. В данном обзоре кратко представлена история развития методов молекулярной механики, а также их последующее применение в компьютерной биологии.
Молекулярная динамика

Молекулярная динамика — не новичок среди биоинформатических дисциплин, и в последние годы ее сильно подвинули подходы на базе искусственного интеллекта. Однако пока ИИ проходит «пик завышенных ожиданий», физически подкрепленные МД-методики достигают «плато продуктивности», позволяя строить корректные модели биомолекул и рассчитывать важные характеристики, используемые, например, в фармацевтической разработке. В этом спецпроекте мы продолжим давно начатый рассказ, уделив внимание и истории, и современному состоянию методики, и ее будущим перспективам.
Партнер спецпроекта — компания BIOCAD, одна из крупнейших российских биотехнологических компаний. BIOCAD заслужил серьезные позиции на мировом фармацевтическом рынке благодаря выпуску лекарственных препаратов на основе антител.
Введение
За последние 30 лет наиболее заметным достижением в современной компьютерной химии и биологии стало развитие вычислительных методов изучения динамического поведения молекулярных систем. По словам знаменитого физика Ричарда Фейнмана, для понимания принципов функционирования живой материи достаточно предположения, «что все состоит из атомов, и что все, что происходит в живом объекте, можно представить в терминах колебаний и смещений атомов» (курсив автора). Другими словами, знание динамического поведения молекулярной системы позволяет пролить свет на механизм её функционирования. С точки зрения физики, наиболее корректным описанием эволюции молекулярной системы во времени является квантово-механическое представление. Однако получить решение уравнения Шредингера из первых принципов (ab initio), даже с учетом некоторых приближений, используя современные компьютеры, практически возможно только для отдельных атомов и небольших молекул. Существуют, правда, подходы, использующие различные приближения и так называемые полуэмпирические методы квантовой химии, также весьма трудоемкие в случае больших систем атомов.
В то же время есть альтернативный путь — рассматривать молекулярную систему с позиции классической ньютоновской механики и при этом описывать её эволюцию во времени с помощью метода молекулярной динамики (МД). В основе метода МД лежит численное решение уравнений Ньютона для набора атомов:
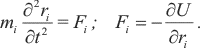
Здесь вторая производная координаты атома (ускорение) пропорциональна силе, действующей на атом, которая, в свою очередь, равна производной потенциальной энергии по координате, взятой с обратным знаком. При этом считается, что эффект движения электронов неявно учитывается в эмпирической функции потенциальной энергии U(r), поэтому в данном случае динамической переменной является только положение ядер как функция времени.
Сегодня использование МД в исследовании различных биомолекулярных систем является обычной практикой. Этот подход широко применяется для изучения структурно-динамических свойств белков, нуклеиновых кислот, липидных мембран. Однако всего 30 лет назад публикация в Nature кратковременного расчета МД бычьего панкреатического трипсинового ингибитора (БПТИ) [1] стала настоящим прорывом в структурной биологии и во многом определила развитие методов молекулярного моделирования. Впрочем, история началась задолго до этого эпохального исследования.
Молекулярная динамика биллиардных шаров
Рождение методов молекулярного моделирования, включающих МД и разновидности метода Монте-Карло (МК), было абсолютно не связано с биологией и происходило в недрах американского ядерного проекта — национальных лабораториях Лос-Аламоса и Ливермора. Первая лаборатория основана в 1943 г. под руководством Роберта Оппенгеймера (Robert Oppenheimer) и стала известна всему миру в связи с проектом «Манхэттен» и последующей бомбардировкой Хиросимы и Нагасаки. Возникновение второй лаборатории в 1952 г. явилось следствием эскалации «холодной» войны между США и СССР. Именно в этих лабораториях ЭВМ стали впервые в мире интенсивно применяться в научных расчетах.
Одним из создателей методов молекулярной динамики по праву можно считать Бэрни Олдера (Bernie Alder) (1925–2020). Работая в начале 50-х аспирантом у известного физика Джона Кирквуда (John Kirkwood) в Калифорнийском техническом институте (CALTECH), он занимался проблемой поведения системы твердых сфер, в которой, подобно биллиардным шарам, частицы взаимодействуют непосредственно при столкновении и двигаются между соударениями как свободные частицы. Возник вопрос — может ли в данной системе наблюдаться фазовый переход из жидкой фазы в твердую? Данная задача не поддавалась простому аналитическому решению, ввиду сложности и нелинейности получаемых интегральных уравнений. Тогда вместе со своим непосредственным руководителем Стэном Фрэнклом (Stan Frankel), который перешел в Калифорнийский институт из Лос-Аламоса, они решили использовать стохастический подход в решении данной задачи. Для этого ими был разработан алгоритм, который позволял исследовать поведение системы твердых сфер путем серии случайных «перетасовок» частиц в некоторой «виртуальной ячейке». Изначально в распоряжении Олдера и Фрэнкла был только механический компьютер IBM, который не позволял далеко продвинуться в расчетах. Однако поскольку Фрэнкл был широко известен в «компьютерных» кругах того времени, для него не составило труда провести расчеты в Англии на первой в мире коммерчески доступной ЭВМ FERRANTI. Это было летом 1950 г. Тем не менее, Олдер так и не увидел фазового перехода в исследуемой им системе.

Рисунок 1. Ник Метрополис (Nicholas Metropolis, 1915–1999) на фоне одной из первых в мире ЭВМ на основе электровакуумных ламп — MANIAC (Mathematical And Numerical Integrator And Computer), 1952 г. Эта аббревиатура придумана самим Метрополисом, который любил давать оригинальные названия своим изобретениям, в частности — знаменитому алгоритму «Монте-Карло», названному так в честь столицы Монако, которая известна на весь мир своим казино. Польский математик Станислав Улам, который работал вместе с Метрополисом, в своей автобиографии «Приключения математика» уточняет, что название было предложено Метрополисом в честь его дяди, который был азартным игроком. Внизу: сноска из оригинальной статьи Метрополиса [2], где упоминается, что Олдер и Фрэнкл также использовали сходный вычислительный подход для изучения фазовых переходов.
Джон Лайлс (John Lyles)
Несмотря на это, созданный ими алгоритм получил впоследствии широкое распространение, и известен миру как молекулярное моделирование методом Монте-Карло (МК). Правда, автором этого подхода считается Николас Метрополис (рис. 1), который параллельно с Олдером работал вместе с супругами Эдвардом и Августой Теллерами, а также Арианной и Маршалом Розенблютами над сходной проблемой в Лос-Аламосе. По поводу истории с авторством Олдер в одном из своих интервью рассказывает, что они вместе с Фрэнклом разработали этот метод независимо от Метрополиса и даже раньше него провели расчеты на ЭВМ. Однако их начальник Джон Кирквуд скептически отнесся к таким исследованиям, что не позволило опубликовать полученные результаты. Метрополис и соавторы опубликовали работу в 1953 г. [2], и вся последующая известность досталась именно им. Это достаточно типичное явление в науке, когда одно и то же открытие делается сразу несколькими независимыми исследователями, но приоритет остается за первым опубликовавшим. Стоит отметить, что Метрополис указал в сносках к своей знаменитой статье, что также над этой проблемой независимо работают Олдер и Фрэнкл (рис. 1). Также стоит отметить, что позднее в своих воспоминаниях Маршал Розенблют указывал на то, что основной вклад в разработку метода моделирования Монте-Карло был внесен именно супругами Розенблют, а не Метрополисом.

Рисунок 2. Бэрни Олдер (стоит), Том Вайнрайт и Мэри Мэнсайн рассматривают осциллограммы движения моделируемых частиц в кабинете Олдера.
архив Эмилио Сегрэ (Emilio Segrè)
После основания Ливерморской лаборатории в 1952 г. Олдер перешел в эту организацию, работая также по совместительству в университете Беркли (Berkeley University of California). Ему пришлось сменить область научных интересов и даже заняться экспериментальной работой на станции по изучению взрывов. Тем не менее, проблема фазового перехода в системе твердых сфер и неудачи с использованием МК в ее исследовании не давали Олдеру покоя. В 1955 году он вновь занялся этой задачей. Совместно с Томом Вайнрайтом (Tom Wainwright) он использовал динамический подход в исследовании фазовой диаграммы системы твердых сфер (рис. 2). Расчеты МД даже для простейшей системы в то время были значительно более трудоемкими, чем стохастический поиск методом МК.
Поначалу многие коллеги отнеслись скептически к их затее. Группой Олдера была разработана первая программа для расчета МД — STEP. Были потрачены тысячи часов расчетов с использованием STEP для накопления необходимой статистики. Вычисления проводились на компьютерах UNIVAC и на IBM 704 (рис. 3). Поскольку компьютерное время было крайне ограниченно, Олдеру приходилось даже обращаться к своим знакомым, имеющим доступ к ЭВМ, с просьбой использовать все свободное машинное время для расчетов STEP.

Рисунок 3. UNIVAC 1 использовал 5200 электровакуумных ламп, весил 13 тонн, потреблял 125 кВт электроэнергии и мог выполнять около 1905 операций в секунду, работая на тактовой частоте 2,25 МГц. Центральный комплекс (т. е. только процессор и память) имел размеры 4,3×2,4×2,6 метров. Вся система занимала площадь в 35,5 м2. Вверху: Макет UNIVAC 1, хранящийся в Смитсоновском Музее Национальной Американской истории. На вставке внизу: Управляющая консоль ЭВМ.

Рисунок 4. Осциллограмма движения частиц в области фазового перехода. Результаты расчетов МД. Отчетливо видны упорядоченные (кристалл) и неупорядоченные (жидкость) области
Наконец к 1957 году задача была решена. В системе твердых шаров наблюдались одновременно области твердого тела и жидкости (рис. 4). Вышедшая в том же году публикация стала первой работой по использованию расчетов МД [3]. На это раз первенство в разработке метода осталось за Олдером. Безусловно, важную роль в успехе исследования сыграло создание эффективного алгоритма расчета, реализованного в STEP. При этом, по словам Олдера, он сам не занимался программированием, считая это «грязной работой». Поэтому большие заслуги в разработке STEP принадлежат двадцатилетней на тот момент Мэри Мэнсайн, упорно работавшей над программой. Ряд революционных подходов в решении динамических уравнений, в частности, алгоритм поиска ближайших соседей в системе шаров, позволил существенно ускорить вычисления. Надо сказать, что задача о фазовом переходе в системе твердых сфер была со временем решена и с использованием МК. Причины неудач в первых попытках Олдера как раз крылись в использовании неоптимального алгоритма расчета.
От биллиардных шаров к реальным атомам

Рисунок 5. Анесур Рахман (Aneesur Rahman, 1927–1987), американский физик индийского происхождения, получил физико-математическое образование в Кембридже, защитил диссертацию в области теоретической физики в Лувенском университете (Бельгия). С 1969 г. в течение 25 лет работал в американской Национальной Аргоннской лаборатории. Поскольку программный код, использованный Рахманом для расчетов МД, лег в основу многих последующих программ, в зарубежной литературе его часто называют «отцом молекулярной динамики». Учитывая особые заслуги Анесура Рахмана в развитии методов вычислительной физики, Американское физическое общество при поддержке компании IBM в 1992 г. учредило его именную премию. Премия в размере $5000 ежегодно вручается исследователям из разных стран за достижения в области компьютерной физики и молекулярного моделирования.
сайт премии
Дальнейшее развитие метода МД шло по нескольким направлениям. Одно из них было связано с изучением поведения не абстрактных сфер, а реалистических атомарных систем. Пионерской работой в данной области стали расчеты жидкого аргона, проведенные Анесуром Рахманом (Aneesur Rahman, рис. 5) [4]. В системе, состоящей из 864 атомов, взаимодействие частиц определялось не только их столкновениями, но также дополнительным парным потенциалом Ленарда-Джонса, соответствующим Ван-дер-Ваальсовой энергии взаимодействия атомов. Поскольку Рахман работал в американской Национальной Аргоннской лаборатории, занимающейся стратегическими вопросами ядерной энергетики, в его доступе были мощные вычислительные ресурсы. Стоит отметить, что в отличие от лабораторий в Лос-Аламосе и Ливерморе, Аргоннская лаборатория никогда не занималась разработкой оружия и исследовала «мирный атом», в частности, проектировала ядерные реакторы электростанций. Расчеты жидкого аргона были проведены с использованием новейшего компьютера CDC 3600, уже к тому моменту имевшего компилятор для языка программирования Фортран-66. Общая длительность МД-траектории (последовательного набора координат и скоростей системы), полученного Рахманом составила ~1 пс (10−12 с).

Рисунок 6. Лу Верле (1931–2019). Помимо исследования жидкостей, занимался изучением истории физики. В частности, им написана книга «La Malle de Newton» посвященная проблемам мировоззрения Исаака Ньютона, состоящего из хитрых переплетений научного и религиозного сознания.
Исследования Ван-дер-Ваальсовых жидкостей с помощью метода МД нашли продолжения в работах французского физика Лу Верле (Loup Verlet, рис. 6) из Университета Пари-Сюд (L’Université Paris-Sud). В 1967 г. Верле рассчитал фазовую диаграмму для жидкого аргона, а также на основании компьютерного эксперимента определил для такой жидкости ряд характерных корреляционных функций, которые давали хорошее согласие с разработанной ранее теорией жидкого состояния [5]. Кроме того, заслугой Верле является разработка эффективного метода численного интегрирования уравнений движения (алгоритм Верле), согласно которому находят координаты каждого атома на основании значения координат в два предшествующих момента времени. Это позволяет не проводить решение дифференциальных уравнений для вычисления скоростей на каждом шаге МД, а получать их на основании разностного уравнения, также предложенного Верле. Такой алгоритм помогает существенно экономить компьютерное время при расчете МД.
4Метод эмпирических силовых полей. Моделирование биомолекул

Рисунок 7. Шнеур Лифсон (1914–2001). Израильский физик, автор более 130 работ в области физики полимеров, статистической термодинамики, внутри- и межмолекулярных взаимодействий, а также теоретической молекулярной биологии.
Существенный прорыв в развитии вычислительных подходов в изучении реальных молекул стал возможен после того, как израильским физиком Шнеуром Лифсоном (Shneior Lifson) из Вейцмановского института в середине 60-х была предложена концепция самосогласованного силового поля (CFF — consistent force field).
Идея заключалась в использовании набора простых термов потенциальной энергии для расчета различных свойств молекул. Таким образом, потенциальная энергия молекулы описывается набором уравнений (рис. 8), параметрами которых служат константы (длины и энергии межатомных связей, значения валентных и двугранных углов и др.), полученные экспериментально или с помощью методов квантовой химии. Нобелевский лауреат, английский биохимик Джон Кендрю (John Kendrew [6]), узнав об идее Лифсона, увидел большие возможности использования CFF в изучении молекул белков и нуклеиновых кислот. В 1967 г. он направил одного из своих аспирантов работать в группу Лифсона. Этим аспирантом был Майкл Левитт (Michael Levitt, рис. 9). Он начал работу по созданию компьютерной программы, в которой была бы реализована идея Лифсона. Вейцмановский институт в то время обладал мощными вычислительными ресурсами. В частности, в 1963 г. была введена в пользование ЭВМ GOLEM I, разработанная и собранная местными инженерами. Особенность этого компьютера, названного по мотивам еврейского фольклора, заключалась в возможности обработки слов размером 75 бит (мировой рекорд того времени).
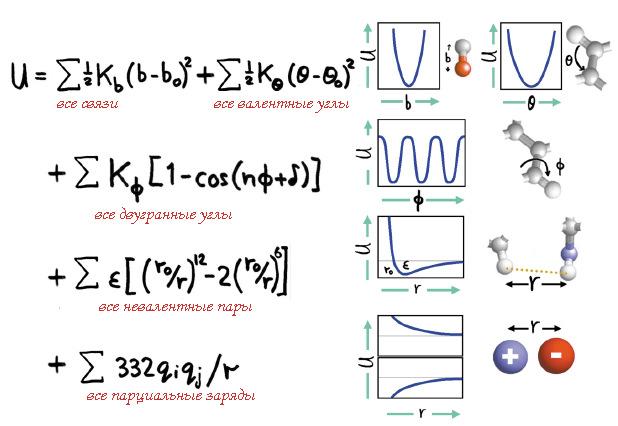
Рисунок 8. Описание потенциальной энергии молекулярной системы, предложенное Лифсоном. Лифсон также предложил упрощенное описание для водородной связи, как некое эффективное электростатическое взаимодействие между двумя парциальными зарядами.
[8], рисунок адаптирован

Рисунок 9. Майкл Левитт (род. 1947). Профессор Стэнфордского университета и заведующий Лабораторией компьютерной структурной биологии. Один из основоположников методов компьютерного моделирования и исследования структур биомолекул (преимущественно белков). Автор большого количества публикаций. Средний индекс цитирования его работ составляет порядка 92 ссылок на одну статью.
За два месяца Левитту удалось написать программу, также названную CFF, которая позволяла рассчитывать энергию и силы в любой молекулярной системе. Следуя наставлениям Кендрю, Левитт провел первые в мире расчеты потенциальной энергии белков. Для этого были использованы уже полученные к тому времени с помощью рентгеноструктурного анализа пространственные структуры миоглобина и лизоцима. Вернувшись в Кэмбридж в 1968 году, Левитт продолжил свою работу в Лаборатории молекулярной биологии, в которой тогда одновременно работало три нобелевских лауреата — Френсис Крик (Francis Crick), Фрэд Сэнгер (Fred Sanger) и Кендрю. Дальнейшая работа Левитта была связана с построением модели пространственной структуры транспортной РНК (тРНК). Существование этой молекулы было предсказано Криком за десять лет до того, как начали проводиться активные исследования ее структуры и функций. тРНК содержит ~2000 атомов, поэтому, когда Левитт у себя дома построил CPK-модель из конструктора [6], вес «молекулы» составил почти 50 килограмм. Транспортировать такое сооружение, по словам Левитта, было нелегко — ему даже пришлось воспользоваться окном, чтобы спустить «молекулу» из своего домашнего кабинета на первый этаж. Позднее в лаборатории Левитт заново построил тРНК уже в виде проволочной модели [6], которую использовал для определения взаимного расположения всех атомов в молекуле. Оптимизированная с помощью программы CFF, модель тРНК была вскоре опубликована [7]. Однако структура нуклеиновых кислот в то время казалась достаточно простой и очевидной, и поэтому более интригующей тематикой были принципы организации полипептидной цепи. В дальнейшем Левитт активно работал над проблемой сворачивания белковых молекул и механизмов ферментативных реакций, используя различные методы конформационного анализа, основанные на концепции силового поля. Его пионерские работы предваряли множество последующих исследований в области структурной биологии, активно проводимые уже на протяжении четверти века.
Программа CFF, написанная Левиттом ещё в годы аспирантуры, оказалась «впутанной» в историю развития методов МД. Как он писал позднее, CFF «путешествовала по миру самостоятельно», появляясь в разных лабораториях [8]. В 1971 году в лаборатории Мартина Карплюса (Martin Karplus, рис. 10) в Гарварде, Брюс Джелин (Bruce Gelin), только что вернувшийся со службы в американской армии, начал работу по переписыванию кода CFF. Впоследствии Левитт, увидевший новую версию своей программы, был поражен элегантностью написанного Джелиным кода: «Этот вариант сильно отличался: пока я осваивал программирование по стандартному руководству IBM FORTRAN II, Брюс Джелин сильно преуспел в этом вопросе. Я до сих пор помню свое восхищение, когда увидел эту версию своей программы — многие названия переменных остались от меня, однако все в целом выглядело намного элегантнее!» [8]. Программа, написанная Джелином, позволила провести первый расчет молекулярной динамики белка, который был опубликован Эндрю Маккаммоном (Andrew McCammon, рис. 10) и Карплюсом в 1977 г. [1]. Работа стала настоящим прорывом, свидетельствуя о наступлении новой эры в компьютерных исследованиях молекулярных систем. С этого момента использование силовых полей для расчетов МД биомолекул стало стандартной практикой.
Как ни странно, свои вычисления Маккаммон и Карплюс провели не в Америке, а во французском международном вычислительном центре CECAM (Centre Européen de Calcul Atomique et Moléculaire), организованном в конце 60-х при университете Пари-Сюд, где в то время активно занимались изучением динамики жидкостей (в частности, Верле — см. выше). Работа в этом центре была организована по весьма оригинальной схеме — на несколько месяцев собиралась рабочая группа ученых из разных стран для решения какой-нибудь конкретной задачи.

Рисунок 10. Мартин Карплюс (1930–2024, слева) и Эндрю Маккаммон (род. 1947). Карплюс был профессором на факультете химии и химической биологии в Гарварде, а Маккаммон руководит группой молекулярного моделирования в Университете Сан-Диего.
Код, написанный Брюсом Джелином, впоследствии лег в основу нескольких МД-программ следующего поколения, которые активно используются и по сей день: CHARMM (Chemistry at HARvard Molecular Mechanics) — разработка группы Карплюса, AMBER — группа Питера Коллманна (Peter Kollmann) из Калифорнийского университета (UCSF) и Discover — компания-производитель научного программного обеспечения Biosym (сейчас — Accelrys), организованная Арнольдом Хаглером (Arnold Hagler).
Динамика белковой глобулы
В чем же все-таки заключалась революционность работы Маккаммона и Карплюса? Вряд ли современного читателя впечатлят полученные ими результаты и используемые методы расчетов. Объектом исследования авторы выбрали небольшой белок БПТИ, состоящий из 58 аминокислотных остатков (рис. 11) и содержащий три дисульфидные связи, которые стабилизируют молекулу. В качестве стартовой конформации авторами была взята кристаллографическая структура БПТИ, полученная несколькими годами ранее.
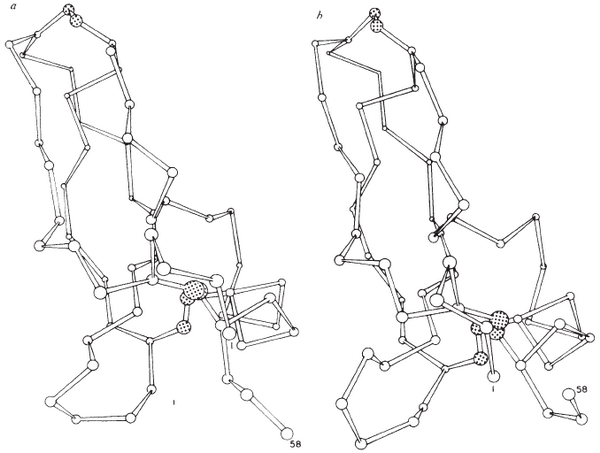
Рисунок 11. Кристаллографическая конформация БПТИ (слева) и конформация белка после 3,2 пс расчетов МД. В 1977 г. молекулярная графика была в зачаточном состоянии, поэтому исходно структуры белка были построены в виде линий на плоттере, а затем дорисованы художниками вручную.
Выбранная ими схема расчета МД в вакууме, в целом напоминает современные методики. Шаг интегрирования динамических уравнений был выбран равным 1 фс (10−15 с) — заведомо меньше самых быстрых движений в белке (колебания протонов). Поскольку исходная конформация БПТИ не находилась в энергетическом минимуме, чтобы понизить потенциальную энергию, часть ее была переведена в кинетическую. В результате белок за несколько сотен шагов МД «нагрелся» от 0 до 285 K. Последующие 9 пс (9000 шагов) основного расчета температура в системе колебалась в районе 295 K (22° C — комнатная температура). Стоит отметить, что «температура» в МД является важным понятием и в соответствии с молекулярно-кинетической теорией может быть рассчитана через кинетическую энергию атомов (их скорости). В современных расчетах используют специальные алгоритмы — «термостаты», которые позволяют поддерживать температуру в системе около заданного значения. Их принцип обычно основан на введении в уравнения МД дополнительной знакопеременной силы трения, зависящей от скорости атома. Эта сила может либо разгонять атомы, либо тормозить в зависимости от разницы между желаемой и фактическими температурами системы. Один из первых подобных алгоритмов, позволяющих проводить расчеты в реалистичных условиях с постоянной температурой несколькими годами позже был предложен Германом Берендсеном (Herman J.C. Berendsen, рис. 12) [9].

Рисунок 12. Герман Берендсен (1934–2019). Холст, масло. Профессор Берендсен был одним из самых авторитетных ученых в области компьютерного моделирования молекул. Автор более 270 публикаций, многие из которых обладают очень высоким индексом цитирования. Член Голландской Академии Искусств и Науки. Заслуженный профессор (в отставке) в области физической химии в Гронингенском Университете (Голландия). В его группе в 80-х годах разработано силовое поле Gromos и программный пакет для МД GROMACS.
Несмотря на то, что расчеты БПТИ Маккаммона и Карплюса были весьма кратковременными и проводились в нереалистичных для белковой глобулы условиях (отсутствие растворителя, непостоянная температура и пр.), ряд выводов, сделанных авторами на основании свой работы, имел большое значение для развития теоретических представлений о принципах организации молекулы белка. В частности, анализ динамического поведения атомов БПТИ в процессе МД позволил им установить, что внутренняя организация белковой глобулы по своим динамическим свойствам ближе к жидкости, чем к твердому телу. При этом ими было постулировано, что внутримолекулярные движения в белке имеют диффузионный характер, или как более точно было сформулировано позднее — характер ограниченной диффузии. Кроме того, сам факт, что с помощью компьютерных расчетов можно наблюдать за структурно-динамическими свойствами биомолекул на атомном уровне, подвиг многих ученых на активные исследования в данной области. Количество работ по МД белков и, чуть позже — ДНК, стремительно выросло за несколько следующих лет. Уже через два года Макаммон и Карплюс опубликовали статью, в которой длина траектории МД для БПТИ была на порядок больше (100 пс) [10]. В те годы ими также были исследованы вопросы об учёте растворителя в расчетах [11], характере связывания кислорода с молекулами гемоглобина и миоглобина [12].
Заключение
В настоящее время использование методов МД в исследовании различных биомолекулярных систем стало обычным явлением. Ежегодно выходят тысячи публикаций, посвященных данной тематике. Длительность расчетов часто достигает нескольких микросекунд (10−6 с), а размеры моделируемой системы — нескольких миллионов атомов. При этом объектом исследования являются уже не отдельные молекулы, а сложные молекулярные комплексы, например, белки, встроенные в многокомпонентные мембраны в ячейках с молекулами воды и различными ионами [13], и даже такие сложные молекулярные машины, как рибосома [14] (рис. 13). Безусловно, наблюдаемый прогресс в области моделирования биологических систем, по сравнению с работами тридцатилетней (и тем более — полувековой) давности, стал возможен благодаря стремительной эволюции компьютерной техники. Однако стоит отметить, что основные концепции и практически весь математический аппарат МД были разработаны в те далекие годы, когда исследователи даже не представляли фантастических вычислительных возможностей будущего.
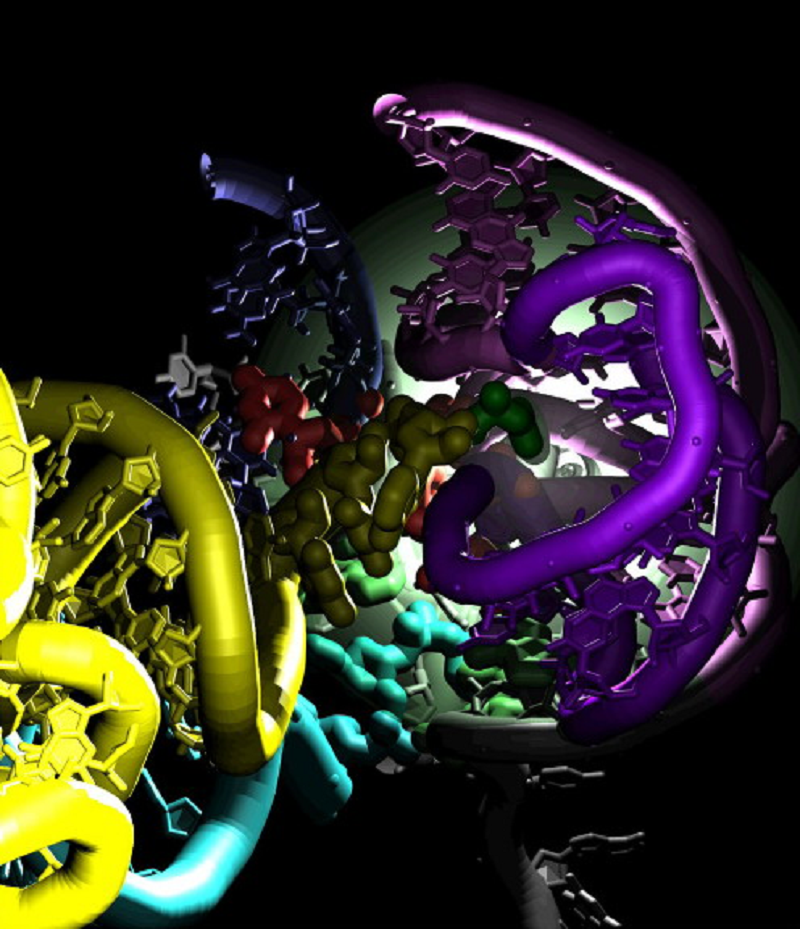
Рисунок 13. Проникновение 3’-CCA конца аминоацил-тРНК (желтый цвет) в пептидил-трансферазный центр большой субъединицы рибосомы. Результаты расчетов МД. Темно зеленым окрашена аминокислота, ковалентно связанная с тРНК. Остальные цвета соответствуют различным фрагментам рибосомальной субъединицы.
Литература
- J. Andrew McCammon, Bruce R. Gelin, Martin Karplus. (1977). Dynamics of folded proteins. Nature. 267, 585-590;
- Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, Edward Teller. (1953). Equation of State Calculations by Fast Computing Machines. The Journal of Chemical Physics. 21, 1087-1092;
- B. J. Alder, T. E. Wainwright. (1957). Phase Transition for a Hard Sphere System. The Journal of Chemical Physics. 27, 1208-1209;
- A. Rahman. (1964). Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev.. 136, A405-A411;
- Loup Verlet. (1967). Computer "Experiments" on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev.. 159, 98-103;
- На заре молекулярной графики;
- MICHAEL LEVITT. (1969). Detailed Molecular Model for Transfer Ribonucleic Acid. Nature. 224, 759-763;
- Michael Levitt. (2001). . Nat. Struct Biol.. 8, 392-393;
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola, J. R. Haak. (1984). Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics. 81, 3684-3690;
- M. KARPLUS, J. A. MCCAMMON. (1979). Protein structural fluctuations during a period of 100 ps. Nature. 277, 578-578;
- Peter J. Rossky, Martin Karplus. (1979). Solvation. A molecular dynamics study of a dipeptide in water. J. Am. Chem. Soc.. 101, 1913-1937;
- D.A. Case, M. Karplus. (1979). Dynamics of ligand binding to heme proteins. Journal of Molecular Biology. 132, 343-368;
- David L. Bostick, Charles L. Brooks III. (2007). Deprotonation by Dehydration: The Origin of Ammonium Sensing in the AmtB Channel. PLoS Comput Biol. 3, e22;
- K.Y. Sanbonmatsu, C.-S. Tung. (2007). High performance computing in biology: Multimillion atom simulations of nanoscale systems. Journal of Structural Biology. 157, 470-480;
- Michael G. (1997). An interview with Bernie Alder. Lawrence Livermore national laboratory;
- David A. Case. (2000). Perspective on "Dynamics of folded proteins". Theoretical Chemistry Accounts: Theory, Computation, and Modeling (Theoretica Chimica Acta). 103, 332-334.