Пространственно-временное моделирование в биологии
01 августа 2012
Пространственно-временное моделирование в биологии
- 7689
- 3
- 5
Адекватное представление свойств системы на разных масштабах — ключевой момент в пространственно-временном моделировании
работа Э.М. Эшера
-
Авторы
-
Редакторы
Темы
Долгое время биология была описательной и феноменологической наукой, мало приспособленной для прогнозирования и рационализации наблюдаемых явлений. С появлением компьютерной техники математика, наконец, стала осваиваться на такой, на первый взгляд, от нее далекой территории. Изначально, наиболее востребованными в биологии были методы математической статистики, которые позволяют корректно обработать данные экспериментов и оценить статистическую значимость делаемых выводов. Однако со временем, с подачи химии и физики (или биохимии и биофизики) в биологии стали использоваться сложные математические модели, позволяющие не только обрабатывать данные реальных экспериментов, но и способные предсказывать протекание биологических процессов в ходе виртуальных (in silico) экспериментов. Вниманию читателей предлагается перевод статьи Иво Сбальцарини, переработанной специально для «Биомолекулы» и рассказывающей о современных подходах в компьютерном пространственно-временнóм моделировании биологических систем.
1. Введение
Пространственно-временное моделирование — это описание развития процессов одновременно в пространстве и во времени. В более простом случае динамику системы «как она есть» можно описывать только во времени: и такой подход обычно используется в химической кинетике или моделировании метаболических процессов. В настоящее время задача пространственно-временного моделирования биологических процессов решается с применением современных суперкомпьютеров. Существующие высокопроизводительные методики, способные корректно обрабатывать большие объемы данных, также позволяют проводить такие виртуальные (in silico) эксперименты, какие в реальности проделать невозможно. Использование компьютера значительно расширяет пределы, в которых можно изменять параметры и проводить наблюдения. Вычислительные эксперименты помогают узнать больше о системах, слишком сложных для анализа вручную, а также позволяют оперировать временными отрезками и расстояниями, которые не доступны в лабораториях.
В качестве примера можно привести изучение молекулярной динамики (МД; см. также «Молекулярная динамика биомолекул. Часть I. История полувековой давности» [122]) в структурной биологии, а также экологические или эволюционно-биологические исследования. В виртуальных экспериментах можно контролировать и измерять все переменные. Поэтому мы можем померить всё, что нужно, и очень точно оценить все ключевые факторы и взаимодействия. В результате мы можем отдельно рассматривать сопряжённые процессы, которые в реальных экспериментах разделить невозможно. Также резко уменьшается или совсем исчезает необходимость непрямых контрольных экспериментов, и легче становится интерпретировать полученные данные. И, наконец, в вычислительных моделях не задействованы живые существа, поэтому можно проводить виртуальные эксперименты, которые в жизни недопустимы по этическим соображениям. В этой статье речь пойдет о применении пространственно-временных компьютерных моделей в области биологии, хотя применяемые методы и концепции используются более широко.
Чтобы разрешить динамический процесс в пространстве, необходимо значительно увеличить число степеней свободы (переменных), которые нужно отслеживать. Возьмём, к примеру, биохимическую реакцию гетеродимеризации. Для химическо-кинетической модели будет достаточно только трех переменных: концентрации димеров и каждого из двух мономеров. Допустим, что мономеры синтезируются в определённых точках в пространстве и свободно диффундируют оттуда в окружающую среду. Следовательно, их концентрация в пространстве изменяется от высокой (рядом с источником) до низкой (вдали от него). Очевидно, что такая детализация значительно увеличивают количество переменных, которое нужно отслеживать в модели. Если при этом нас интересуют локальные концентрации в тысяче точек, то нам придётся отслеживать три тысячи переменных. Более того, реакции, протекающие в разных точках пространства, зависят друг от друга. Каждая локальная реакция может влиять на остальные, так как мономеры и димеры распространяются в пространстве посредством диффузии. Это приводит к тому, что сложность пространственно-временных моделей быстро возрастает. На самом деле, в теории не существует максимального числа точек в пространстве, которые мы можем использовать для разрешения пространственных структур в концентрационных полях. Если мы возьмём бесконечно много точек, тогда система будет смоделирована как непрерывное множество (континуум). На данный момент создан мощный математический инструментарий, который эффективно работает с пространственно-временными моделями и воспроизводит их. В данной работе мы не ставили цель подробно описать каждый из этих методов, поэтому предлагаем читателю общий обзор со ссылками на специализированную литературу. Но сначала мы вспомним некоторые особенности и предпосылки использования пространственно-временного моделирования в сфере биологии и медицины.
Пространственно-временное моделирование позволяет нам описывать природу в четырёх измерениях — в трёх пространственных измерениях и во времени. Для динамического развития системы необходимо время и резервуары (накопители); кроме того во многих биологических процессах существенную роль играют трёхмерные (3D) пространственные характеристики. Представьте, к примеру, как хищники рыщут по лесу в поисках добычи, как кровь течёт по нашим артериях, как электромагнитные поля возникают в мозге, или такой неприятный феномен, как распространение заболевания и превращение его в эпидемию. Для всех приведенных примеров необходимо учитывать пространственное распределение многих параметров. При определении местонахождения в мозге участка, ответственного за эпилепсию, информация об общей плотности электрического тока во всём мозге практически бесполезна, так как нам нужно знать, где находится этот участок. Подобные примеры в изобилии встречаются в биологических системах любых масштабов: от вышеупомянутых взаимоотношений типа «хищник—жертва» в экосистемах до морфогенеза [34], [40], [48], [68], [118] и внутриклеточных процессов, а от них — до уровня отдельных молекул (например, конформационных изменений в белках).
На внутриклеточном уровне примерами могут служить проникновение вирусного материала в клетку [19], [109] и его перенос [20], [36], [69], передача сигнала внутри клетки [60], [70] и диффузия белков в различных клеточных компартментах [17], [61], [99], [120], [100]. Пространственная организация очень важна, так как один и тот же белок может действовать по-разному в зависимости от того, в каком внутриклеточном компартменте он находится. Самый известный пример такого белка это, наверное, цитохром c, который, находясь в митохондрии, играет важную роль в клеточном дыхании, а, попав в цитоплазму, запускает процесс запрограммированной гибели клетки (апоптоз) [1]. Другим примером может служить роль трансмембранной передачи сигнала при морфогенезе. Константы белковой диффузии различаются недостаточно, чтобы сформировались структуры Тьюринга [118], поэтому очень важен медленный транспорт через мембраны между компартментами [86]. Вот ещё несколько примеров пространственно-временных процессов, теперь уже на уровне множества клеток: рост опухоли [13], [46], [64], распространение вируса в ткани и система передачи сигнала между клетками [41], в том числе феномен, известный как бактериальный «кворум-сенсинг», микро-процесс, определяющий, например, макро-эффект биолюминесценции в теле кальмаре [75]. Если принять во внимание, что пространственно-временные процессы широко распространены и очень важны, то нет ничего удивительного в том, что на сегодняшний день существует несколько масштабных проектов по разработке программного обеспечения для моделирования пространственно-временных процессов в биологии. В качестве примеров таких программ для вычислительной клеточной биологии [24], [107] можно назвать E-Cell, MCell и Virtual Cell (см. также: «Биологи создали самую сложную виртуальную клетку»).
2. Свойства биологических систем
Математик, решивший смоделировать пространственно-разрешённые процессы в биологических системах, например в географически структурированных популяциях, многоклеточных организмах или клеточных органеллах, столкнётся с рядом уникальных проблем. Обычно в таких случаях мы слышим: «Да это потому, что биологические системы сложны». Биохимические сети, экосистемы, биологические волны, синхронизация клеток сердца, да и сама жизнь — всё это находится в многомерной нелинейной области конфигурационного пространства динамических систем [113], и там же располагается квантовая теория поля, нелинейная оптика и турбулентные потоки. Все эти темы изучены недостаточно. Сейчас наши познания в этих областях близки к пределу, и в течение многих лет нам предстоит находить ответы на поставленные ими вопросы. Почему всё происходит именно так, и что мы понимаем под термином «сложный»? У биологических систем есть несколько свойств, которые затрудняют работу с такими системами:
- многомерность (или бесконечное число измерений в пределах континуума);
- регуляция;
- наличие сложных пространственных форм;
- нелинейность;
- сопряжённость процессов на разных масштабах и в разных подсистемах;
- пластичность во времени (динамическая эволюция во времени);
- неравновесность.
Именно благодаря этим свойствам биологические системы — крепкий орешек для существующих технологий моделирования и вычислительных экспериментов. Поэтому такие системы прекрасно стимулируют разработку новых методик и теоретической базы для них. Проблемы, появляющиеся при анализе пространственно-временных биологических систем, следут решать одновременно несколькими способами: с помощью методов численного моделирования, вычислительных алгоритмов и разработки программного обеспечения [115]. Что касается численных методов для анализа биологических систем, они доллжны быть пригодны для работы с многомасштабными системами [3], [14], [52], [53], [71] и учитывать топологические изменения в системах со сложной геометрией. Также тут необходимы компьютерные алгоритмы, достаточно совершенные, чтобы работать с большим количеством степеней свободы, и программы, способные надёжно и эффективно использовать эти алгоритмы на многопроцессорных машинах [97].
2.1. Степень многомерности и степени свободы
В биологических системах большое количество измерений (степеней свободы) обусловлено тем, что у них, как правило, больше частей, компонентов и типов взаимодействий, чем у классических технических средств, использующих электричество или гидромеханику [115]. При использовании прямого численного моделирования необходимо чётко отслеживать все степени свободы. В непрерывных системах каждая точка в пространстве прибавляет дополнительные степени свободы, что в итоге приводит к беконечному числу измерений. Такие системы нужно дискретизировать, иными словами, следует уменьшить число степеней свободы до допустимого в компьютерном моделировании с помощью направленного отбора характеристических измерений. В расчетах будут использованы только выбранные измерения, что позволит экстраполировать полученные результаты на исходную бесконечномерную систему. Дискретизация должна быть самосогласована: при бесконечном увеличении числа измерений дискретизированная система приближается к исходной системе.
В дискретных биологических системах число степеней свободы уже ограничено, поэтому их иногда можно моделировать напрямую. В случае, когда степеней свободы слишком много, как, например, при отслеживании перемещений всех атомов в белке, нам часто снова приходится уменьшить их число, чтобы повысить эффективность моделирования. В этом случае можно объединить несколько степеней свободы в одну и отслеживать поведение всей группы. Такая технология, называемая «увеличение зернистости», значительно уменьшает вычислительные затраты и позволяет моделировать очень большие многомерные системы — например, участки липидных бислоев с белковыми включениями [80], [88], действие на них многих молекул антимикробных пептидов [82] или филаменты актина [15]. «Увеличение зернистости» расширяет возможности молекулярного моделирования во временном и линейном масштабе для биологических задач.
2.2. Регуляция
В биологических системах роль случая невелика, и это удивительно, так как мы знаем, что молекулярные процессы, факторы природной среды и фенотипическая вариабельность по своей природе стохастичны. Однако исходные колебания в этих процессах в большинстве случаев предваряют переход к регулируемому детерминированному поведению, как было показано, например, для генных регуляторных сетей [49]. В биологических системах в дополнение к непрямой регуляции посредством бистабильности и стохастических колебаний широко распространены регуляция с использованием обратной связи и цепи упреждения. Механизмы регуляции крайне важны как для передачи сигнала (сигнальной трансдукции) в отдельных клетках, так и для всей эволюции, как её понимал Дарвин. Данные теории регуляции показывают, что упомянутые цепи могут корректировать динамические свойства системы, изменять её стабильность или устойчивость, либо инициировать мультиустойчивое состояние, которое позволяет системе адаптироваться к изменениям и возмущениям, идущим извне [49]. Необходимость учитывать все факторы представляет собой огромную проблему для моделирования, так как многие из возможных механизмов регуляции до сих пор неизвестны или недостаточно изучены.
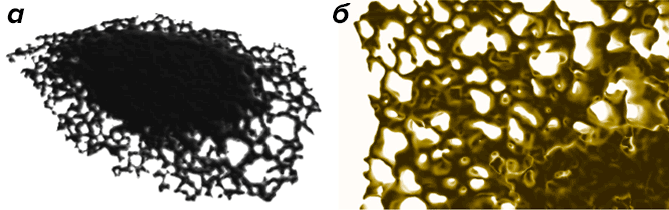
Рисунок 1. Эндоплазматический ретикулум. а — Изображение трёхмерной компьютерной модели структуры эндоплазматического ретикулума (ЭР) живой клетки [100]. б — Крупный план модели ЭР демонстрирует сложность структуры этого внутриклеточного органоида.
2.3. Сложность форм
Для биологических систем зачастую характерны неправильные, подвижные или изменяющие свою форму очертания. Процессы, происходящие на нелинейных поверхностях, могут объединяться с процессами, присходящими в замкнутых пространствах, и сами поверхности часто изменяют топологию при, например, слиянии или разделении внутриклеточных компартментов. Сложные топологии встречаются в системах любых размеров, к ним также относятся таксономические и филогенетические деревья с пре-фрактальной структурой [12], участки стабильного роста популяции в экосистемах [77], лёгочные и артериальные деревья [35], формы нейронов [111], цитоплазматическое пространство [4], скопления внутриклеточных везикул [54], электрический ток, текущий через ионные каналы в клеточных мембранах [59], конформации белковых цепей [57], и структуры белков [56]. Мало того, что сложные топологические формы сложно смоделировать с помощью компьютера, они ещё и накладывают граничные условия на пространственно-временные процессы, и эти условия могут качественно изменять динамику макропроцессов. Диффузия в прихотливой формы компартментах (например, в эндоплазматическом ретикулуме (ЭР, рисунок 1) может быть нестандартной, несмотря на то, что на уровне отдельных молекул она вполне описывается классическими закономерностями [94–96], [100].
2.4. Нелинейность
Обычные в биологии явления — взаимодействие, сотрудничество или конкуренция — заставляют систему вести себя нелинейно. Теория линейных систем, в том виде, в каком она преимущественно используется и преподается в физике и инженерном деле, не может верно описать множество процессов, начиная от взаимодействия репрессоров в генных сетях и регулирующих отношений хищник—жертва в экосистемах, и заканчивая волнообразными изменениями концентрации кальция в клетках. Нелинейные системы зависят от числа степеней свободы и обнаруживают эффекты, которые не наблюдаются в линейных системах. Среди таких эффектов могут быть бифуркации, нелинейные колебания, а также неупорядоченность и фракталы. Нелинейные модели трудно решаются по определению. Большинство нелинейных моделей вообще невозможно решить аналитически, а обычные вычислительные методики, например, анализ нормальных колебаний, преобразования Фурье или принцип суперпозиции, не работают в нелинейных системах, так как сумма частей такой системы не идентична всей системе целиком [113].
2.5. Сопряжённость процессов на разных масштабах
Сопряжённость процессов на разных масштабах приводит к тому, что некоторые явления, происходящие на микроуровне, например, изменения конформации молекул, могут существенно влиять на поведение системы на глобальном, макроуровне. Именно так обстоит дело со многими биологическими системами — например, биолюминесценция происходит засчёт бактериального кворум-сенсинга [75], или поведение организма меняется, потому что определенные гормоны связываются с рецепторами. У многомасштабных систем есть одно общее свойство — нельзя разделять индивидуальные масштабы и рассматривать их независимо друг от друга. Существует непрерывный диапазон масштабов, в котором взаимодействия сопряжены, что жёстко ограничивает применение компьютерного моделирования. Если мы решим построить прямую численную модель всей системы, нам нужно разрешить её во всех возможных деталях. Если мы захотим смоделировать живую клетку, нам придётся разрешить динамику всех атомов в этой клетке. Отдельная клетка состоит из примерно 1015 атомов, и процессы, имеющие отношение к биологии (такие как сворачивание белка и ферментативные реакции), происходят за тысячные доли секунды. Самые крупные из существующих на сегодня модельных систем, доступных для методов расчета МД, состоят из 1010 атомов [27], при этом временные диапазоны, в которых возможно изучение таких систем с помощью суперкомпьютеров, ограничены наносекундами. Чтобы смоделировать клетку целиком, нам нужна модель в 100 000 раз больше, и которая будет работать с временами в 1 000 000 раз дольше. Нужная компьютерная модель будет как минимум в 1011 раз масштабнее, чем те, что у нас есть на сегодняшний день. Пока такая модель в реальности не существует и не появится ещё много лет. Если представить, что кому-то удалось смоделировать систему целиком с высоким разрешением, ценность таких результатов довольно сомнительна. Такая модель даст большой объём данных, и интересные эффекты на макроуровне, которые мы ищем, будут скрыты за шумом с микроуровней. Чтобы работать сопряженными системами, нам необходимо применять многомасштабные модели [3], [14], [53], [71] и правильно выбирать их уровень детализации.
2.6. Пластичность во времени
Помимо того, что анализ многомерных нелинейных систем не прост сам по себе, эти системы в биологии обычно изменяются во времени. В математической модели такое поведение системы отражается в скачках динамических уравнений или в коэффициентах и функциях, которые меняются во времени. Динамически изменяясь, система может начать вести себя по-другому или перейти в другой режим. Динамика многих процессов в клетке, например, зависит от клеточного цикла; в организме происходят физиологические процессы и изменяют динамику организма в зависимости от возраста и состояния здоровья; а динамическое поведение экосистем зависит от изменений природной среды. Такие системы называются пластичными или изменяющимися во времени. Вопрос, как применять численное моделирование к изменяющимся во времени системам или к уравнениям, которые изменяют свою структуру с течением времени, пока не решен. Чтобы выбранная модель оставалась стабильной, нужно обеспечить согласованность решений в точках перехода.
2.7. Неравновесность
Второй закон термодинамики гласит — энтропия замкнутой системы не может уменьшаться. Живые существа научились избегать распада на составные части за счёт отрицательной энтропии [103]. Учёные давно недоумевают по поводу несоответствий между живым миром и фундаментальными законами термодинамики. Объяснить эти несоответствия можно лишь предположив, что живые системы не находятся в равновесии. Большинство методов статистической физики и термодинамики было разработано для равновесных состояний и поэтому не во всех случаях может применяться для описания живых систем. Некоторые явления, такие как установление полярности клетки или организация клеточной мембраны можно объяснить, только приняв во внимание неравновесные процессы, например, везикулярную рециркуляцию [67]. Мы знаем слишком мало о теоретических основах неравновесных процессов, и от этого понять их становится ещё труднее. Зачастую компьютерное моделирование переходных процессов — единственный доступный метод для изучения неравновесных процессов.
3. Методы пространственно-временного моделирования
Описывать динамические пространственно-временные процессы можно разными способами — всё зависит от нужного уровня детализации и достоверности. В данной статье для характеризации математической модели мы выбрали следующую систему координат: феноменологическая—физическая, дискретная—непрерывная и детерминистская—стохастическая. Все три оси независимы, и возможны любые комбинации. В зависимости от описания выбранной системы можно использовать разные методики. На рисунке 2 представлен обзор наиболее часто используемых методик и примеры динамических систем, описания которых можно подготовить с помощью этих методик.
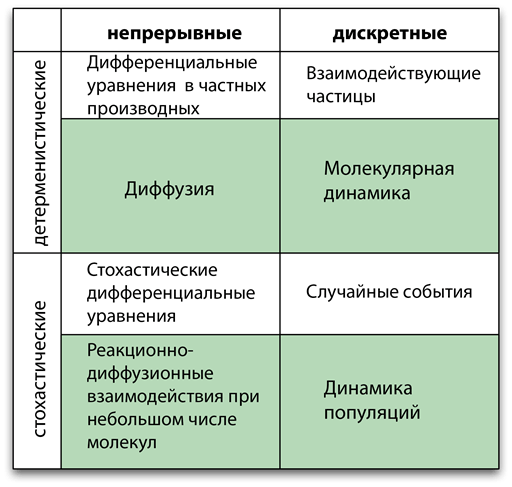
Рисунок 2. Наиболее часто используемые методы моделирования для всех возможных комбинаций непрерывных/дискретных и детерминистских/стохастических моделей. Те же методы применяются и для физических/феноменологических моделей, но в первом случае все модели основываются на принципах физики. В выделенных ячейках даны распространённые примеры применения этих методов.
3.1. Феноменология против физики
Феноменологические модели воспроизводят или приближённо выражают поведение системы в целом, но не объясняют механизмы, лежащие в основе такого поведения. Такие модели могут быть полезными при анализе реакции системы на какое-то известное возмущение, но они не позволят понять, что именно вызвало реакцию. Напротив, физические модели точно воспроизводят механику работы системы. Таким образом, физические модели позволяют предсказать поведение системы в новых непредвиденных ситуациях, они информируют нас о том, как всё работает. Физические модели опираются на основные принципы или законы физики.
3.2. Дискретные модели против непрерывных
Дуализм дискретность-непрерывность связан с пространственным разрешением модели. В дискретной модели каждый элемент системы однозначно определяется как отдельный объект. Как пример можно привести модели МД, в которых чётко отслеживается положение и скорость каждого атома, и атомы рассматриваются как отдельные дискретные объекты. В непрерывной модели во времени и пространстве отслеживается среднее значение среднего поля. Примерами величин поля могут быть концентрация, температура или плотность заряда.
В непрерывных моделях выделяют два типа величин. Величины, чьи значения в гомогенной системе не зависят от усредняющего объёма, называются интенсивными. Например, температура или концентрация. Если литр воды температурой 20 °C разлить в два поллитровых стакана, вода в каждом стакане будет иметь ту же температуру, несмотря на то, что объём её уменьшится вдвое. Температура воды не зависит от её объёма, поэтому температура здесь проявляет интенсивные свойства. Величины, чьи значения в гомогенной системе зависят от объёма, называются экстенсивными. К таким величиным относятся масса, теплота или заряд. Масса каждых 500 миллилитров воды не равна массе исходного литра.
Интенсивные и экстенсивные величины существуют парами: масса—концентрация, температура—теплота, заряд—плотность заряда и так далее. В непрерывных моделях величины поля всегда считаются интенсивными, а величины в дискретных моделях — экстенсивными. Соответствующие интенсивные и экстенсивные величины взаимодействуют посредством усреднения. Концентрацию молекул можно определить, измерив общую массу всех молекул в пределах заданного объёма и разделив её на объём. Такой усредняющий объём можно представить вокруг любой точки пространства, и таким образом мы получим пространственно-разрешённое поле концентрации. Если задать слишком маленький усредняющий объём, отдельные молекулы, входя и выходя из него, создадут резкие скачки значений среднего. С увеличением усредняющего объёма концентрация будет стремиться к какому-то устойчивому значению. Если продолжать увеличивать объём, концентрация снова, скорее всего, начнёт меняться из-за пространственных градиентов в макромасштабе. Рисунок 3 иллюстрирует вышеописанное поведение. Когда объём превышает континуальный предел λ, среднее значение сходится, и влиянием отдельных частиц в микромасштабе становится можно пренебречь. Величина континуального предела подчиняется отношением количества частиц к усреднённому объёму. Если эти частицы — молекулы (например, белки), то параметр λ зависит от их среднего свободного пробега. В области, где вариации поля превышают параметр L, проявляются макроскопические градиенты усреднённого поля в том случае, если поле неоднородно, то есть если его значение изменяется в пространстве. Безразмерный коэффициент Kn=λ/L назывется числом Кнудсена. Непрерывные модели правильно использовать только, когда эффекты на микро- и макроуровнях хорошо разделены, то есть если Kn n >> 1 следует использовать дискретные модели, так как важна каждая частица, и не существует единого континуума. Посередине между этими значениями Kn находится царство мезоскопических моделей [33].
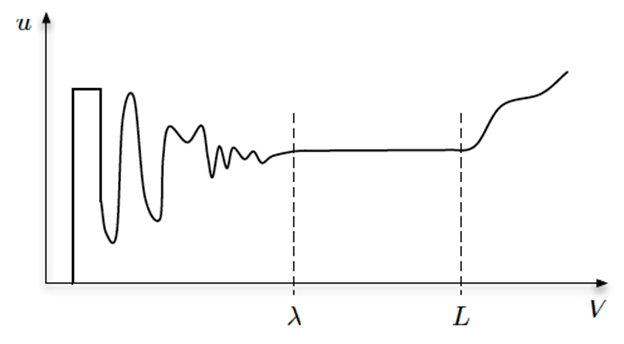
Рисунок 3. Значение параметра u, описывающего объёмно-усреднённую интенсивную величину поля, зависит от величины усредняющего объёма V. В объёмах, меньших, чем континуальный предел λ, среднее значение варьирует из-за воздействия отдельных частиц. В объёмах, больших λ, средняя величина объёма может либо оставаться постоянной, либо постепенно изменяться, если будет превышена величина L (шкала вариаций поля), благодаря влиянию макроскопических градиентов поля.
В непрерывных детерминистических моделях величины поля, чьё развитие в пространстве и времени зависит от некоторых производных от тех же или других величин поля, изменяются плавно (в масштабах, больших L). С помощью полей можно моделировать, например, концентрации, температуры или скорости. Такие модели естественным образом определяются нестационарными дифференциальными уравнениями в частных производных [25], [112], так как производные связаны с существованием интеграторов, а значит резервуаров, в системе. Среди самых ярких примеров непрерывных детерминистических моделей в биологических системах можно назвать модели диффузии, адвекцию, перенос и волны. В дискретных детерминистических моделях присутствуют дискретные объекты, которые взаимодействуют между собой в пространстве и во времени согласно детерминированным правилам. Объекты, взаимодействуя, могут моделировать клетки в ткани [34], отдельные организмы в экосистеме или атомы в молекуле [27]. Такие модели в основном трактуются как системы взаимодействующих частиц или автоматы. Применение для дискретных детерминистических моделей в области биологии можно найти в экологии или структурной биологии.
3.3. Стохастические модели против детерминистических
В биологических системах часто присутствует некая степень случайности, например непредсказуемые изменения окружающей среды, изменения количества молекул при делении клетки или шумы на уровне экспрессии гена. Все эти эффекты можно объяснить с помощью стохастических моделей, в которых выходные данные не полностью определяются текущим состоянием модели и входными данными, а зависят также от колебаний случайного характера. Такие колебания обычно воспроизводятся как случайные числа в заданном статистическом распределении. Непрерывные стохастические модели характеризуются плавными изменениями полей, развитие которых в пространстве и времени зависит от плотностей вероятности — функций некоторых производных полей. В простейшем случае всё сводится к моделированию единственной шумовой состявляющей, например, Гауссовым или постоянным колебаниям в динамике. Чаще всего модели такого типа формально известны как стохастические дифференциальные уравнения (СДУ) [79]. СДУ — это дифференциальные уравнения в частных производных со стохастическими условиями, которые используются для моделирования вероятностных процессов, например распространения эпидемии, сигнальной трансдукции в нейронах [66], [92] или теории эволюции. В дискретных стохастических моделях вероятностные явления связаны, в основном, с дискретными случайными событиями. Характеризуются такие события функциями плотности вероятности. Примером может служить динамика популяции — у отдельных особей есть определённые шансы родиться, умереть, пообедать или стать обедом для кого-то ещё, — а также случайное блуждание диффундирующих молекул или стохастическое возникновение химических реакций. Существуют методики для объединения стохастических и детерминистических моделей в гибридные стохастически-детерминистические модели [2], [93].
4. Методики пространственно-временного моделирования
В зависимости от методики моделирования, выбранной для конкретной системы, возможно использовать разные численные методы для обсчета окончательной модели на компьютере (рис. 2). Перечислить все доступные методики не представляется возможным, но мы хотим обратить внимание читателя на модели, важнейшие в каждой из обсуждаемых выше категорий. Одни и те же численные методы можно ипользовать как в физических, так и в феноменологических моделях.
4.1. Методы, используемые в дискретных стохастических моделях
Дискретные стохастические модели, которые определяются событиями, происходящими в соответствии с неким случайным распределением, можно описывать с помощью алгоритмов вероятностного моделирования (АВМ), например, алгоритма Гиллеспи [31], [32] или какими-нибудь более вычислительно эффективными его вариантами [29], [83–85], [108]. Изначально большинство таких алгоритмов было разработано только для динамики во времени, а обобщены для таких пространственно-временных моделей, как реакционно-диффузионные процессы, они были позже [6], [26], [45], [90], [114]. Большая часть подобных алгоритмов основана на методах Монте-Карло [63], [91] (см. также «Молекулярная динамика биомолекул. Часть I. История полувековой давности»). Таким образом, моделирование вероятностных траекторий превращается в выбор из случайных распределений модели. Чтобы оценить среднюю траекторию или стандартное отклонение, нужно посчитать среднее по множеству для большого количества прогонов модели. В этом кроется фундаментальное ограничение для сходимости методик: O(1/√N), где N — число воспроизведений модели [72]. Для работы с дискретными стохастическими моделями часто используются агентные методики, в которых задействованы случайные агенты. Хорошей иллюстрацией могут служить Броуновские агенты [105].
4.2. Методы, используемые в дискретных детерминистических моделях
Довольно часто для работы с дискретными детерминистическими моделями используются методики, относящиеся к классу конечных автоматов. Самые яркие примеры — это клеточные автоматы [28], [44], [101] и агентные модели [116] (слово «клеточный» в данном случае обозначает клетки (ячейки), используемые в компьютерном алгоритме, и не имеет отношение к биологическим клеткам). В теории конечных автоматов вычислительные ячейки (или агенты) с заданными свойствами распределены в пространстве и взаимодействуют между собой в соответствии с наборами детерминированных правил. Правила взаимодействия привязывают состояние (значение заданных свойств) взаимодействующих ячеек к определённым действиям, которые, в свою очередь, изменяют состояние ячеек. Конечные автоматы — очень мощные и интересные инструменты, с помощью которых небольшое количество простых правил может инициировать очень сложное нелинейное поведение модели. Использовать конечные автоматы можно с разными целями, например, для изучения аспектов поведения индивидуумов при взаимодействии в экосистемах, в области искусственной жизни, для имитации нейронных взаимодействий [44], социальных взаимодействий [74] или механизмов формирования облика при морфогенезе [34].
В МД существует ещё один класс очень важных дискретных детерминистических моделей [27]. В них атомистическое поведение молекул моделируют, чётко отслеживая динамику и расположение всех атомов. В классической МД атомы моделируют как дискретные частицы, которые взаимодействуют между собой в соответствии с детерминированными механизмами, такими как межатомные связи, силы Ван-дер-Ваальса или электростатические взаимодействия.
4.3. Методы, используемые в непрерывных стохастических моделях
Непрерывные стохастические модели определяются стохастическими дифференциальными уравнениями, в этом случае для моделирования можно использовать несколько методов стохастического интегрирования [43], [51], самые примечательные из которых — это метод Эйлера-Маруямы и метод высшего порядка Мильштейна [43]. При этом важно помнить, что каждый прогон модели — это только одна из возможных реализаций определённого стохастического процесса. Для оценки средних значений и отклонений нужно проводить множество независимых прогонов и считать среднее по набору [43]. Многие учёные, работающие в области вычислительной биологии, считают стохастические дифференциальные уравнения нетрадиционным подходом, но этот метод используется намного чаще, чем кажется. Например, моделирование реакционно-диффузионного процесса с помощью стохастических реакций сводится кчисленному решению стохастического дифференциального уравнения [26], [45], [90], [114].
4.4. Методы, используемые в непрерывных детерминистических моделях
Непрерывные детерминистические модели определяются дифференциальными уравнениями в частных производных; такие модели решаются любым методом дискретизации из численного анализа [23], [38]. Наиболее популярные методики — это конечные разности (КР) [110], конечные элементы (КЭ) [87], [121] и конечные объёмы (КО) для законов сохранения [7], [55]. Методы КР основываются на разложениях с помощью рядов Тейлора [50] для пространственных функций поля и аппроксимации дифференциальных операторов с помощью разностных операторов с сохранением первых нескольких членов из ряда Тейлора. Методы КЭ выражают неизвестную функцию поля в заданном функциональном пространстве. Базисные функции этого пространства основываются на многоугольниках, покрывающих расчётную область. Таким образом, для определения неизвестной функции поля нужно решить линейную систему уравнений и определить нагрузку базисных функций на все элементы. В методах КО используются физические законы сохранения, например, сохранения массы или момента. Расчётная область делится на непересекающиеся объёмы, для которых составляются уравнения баланса (изменение объёма равняется тому, что пришло, за вычетом того, что ушло), и для них находится численное решение. У всех этих методов есть одно общее свойство — для их использования требуется расчётная сетка — регулярная или нет — которая дискретизует расчётную область на простые геометрические фигуры — линии (КР), плоскости (КЭ) или объёмы (КО) с нужным уровнем взаимосвязи. Поиск сетки с соблюдением граничных условий и достаточно регулярной, чтобы сохранялись точность и эффективность численных методов, подходящей для областей сложной топологии, которые часто встречаются в биологических системах (рис. 1) может стать серьёзной проблемой. Избежать проблем помогут бессеточные методы частиц [16], [58], [62], [102], в которых дискретизация построена на объектах-точках, не требующих никакой информации о связности. В дискретных моделях очень часто работают с комбинациями частиц, и их преимущества можно использовать при работе с непрерывной областью с помощью методов непрерывных частиц (континуум-частица). Такие методы аппроксимируют функции гладкого поля непрерывной модели посредством интегралов, дискретизируемых на вычислительных элементах, называемых частицами. В дискретных моделях частицы обозначают реальные объекты — молекулы, атомы, животные или клетки. В непрерывных моделях частицы представляют собой материальные точки (точки маркёров Лагранжа) системы, которые возникают в соостветствии с парными взамодействиями, которые описывают физику системы.
Непрерывные процессы пространственной диффузии представляют особый интерес с точки зрения биологии. В физическом смысле, макро-явление диффузии порождается коллективным поведением большого (в теории бесконечно большого) количества микрочастиц, например, молекул, находящихся в броуновском движении [8], [11], [21]. Теория континуума [76] определяет поле концентрации как среднюю массу частиц на единицу объёма для каждой точки пространства (сравните с разделом 3.2). При работе с большим количеством диффундирующих частиц такое определение позволяет создать непрерывную детерминистическую модель для пространственно-временной эволюции поля концентрации в виде дифференциальных уравнений в частных производных. Моделирование диффузионных процессов с помощью частиц хорошо работает как для описания процесса диффузии в пространстве, так и для диффузии в мембранах [98].
При необходимости смоделировать диффузию нескольких видов молекул, между которыми происходит химическая реакция, модель можно распространить на реакционно-диффузионные системы. В таких моделях существование в биологии пространственно распределённых (био)химических реакционных сетей описывается кинетикой реакции при помощи двух подходов: детерминистического или стохастического. У сопряжённых реакционно-диффузионных систем наблюдают необычные параметры стабильности, согласно которым концентрация либо стабильна и формирует структуры Тьюринга [118], либо изменяется как бегущая волна, называемая волной Фишера [89]. Двадцать лет спустя после выхода основополагающей работы Алана Тьюринга [118], Рирер и Мейнхардт сформулировали теорию формирования структур в биологии [30], опираясь на реакционно-диффузионные системы. Они разработали модель Гирера-Мейнхардта, одну из наиболее часто используемых в биологии моделей формирования структур, которая также нашла применение в компьютерной графике [119].
В биологии реакционно-диффузионные модели были впервые использованы для описания морфогенеза [118], развивая идею о том, что реакционно-диффузионное поведение факторов роста объясняет формы и топологии природных объектов. Компьютерные модели, в которых образование структур связывалось с ростом и морфогенезом, работали при помощи, например, гибридных моделей клеточных автоматов и дифференциальных уравнений в частных производных, описывающих формирование нитей и дифференциацию клеток у слизевиков (миксомицетов) [68]. Что касается моделей реакционно-диффузионных структур на поверхностях, то впервые их применили для шарообразных объектов, таких как сферические новообразования [13]. Морфогенез более сложных поверхностей моделировали с помощью метода КЭ, которым решали реакционно-диффузионное уравнение для триангулированных поверхностей [40]. Таким методом можно описывать весьма сложные формы, как, например, ветвящиеся одноклеточные водоросли. Методы КЭ с подвижной сеткой позже стали использовать для прямой связи смещения границы и реакционно-диффузионных структур в непрерывно меняющихся двухмерных областях [65]. Существует и другой подход — в нём образование формы у поверхности описывается с помощью решения внутренней задачи Пуассона [64]. Помимо морфогенеза реакционно-диффузионные модели важны для описания подвижности клеток [37], моделирования клеток [81] и формирования структур в клеточных культурах [73]. Возникают и новые возможности применения этих методов, например, для моделирования путей передачи сигнала в клетке в пространстве и во времени [9]. С 1993 года, когда была опубликована работа Брэя с соавторами [10], предложившими первую модель для описания путей хемотаксиса в кишечной палочке (Escherichia coli) на основе обыкновенных дифференциальных уравнений, компьютерные модели продвинулись в области разрешения пространственных явлений очень далеко. Одна из недавно опубликованных моделей прямо учитывает диффузию ключевой молекулы процесса сигнальной трансдукции в цитоплазматическое пространство [60]. Среди других примеров моделей реакционно-диффузионной передачи сигнала следует упомянуть сетевую модель управления спорообразованием [70] и моделирование меристемы побегов растений [47].
4.5. Компьютерное моделирование объектов со сложной топологией
Объекты со сложными топологиями и поверхностями можно описать с помощью компьютера посредством нескольких методик [18], которые можно сгруппировать в соответствии с характером информации о связности, необходимой для работы. Как пример представлений, основанных на связности, можно привести триангулированные поверхности [104], каждый треугольник в которых должен иметь информацию обо всех остальных треугольниках, которые с ним связаны. В случае поверхностей со сложными формами выяснение информации о связности требует много вычислительного времени, так что такие модели лучше использовать в связке с численными методами, работающими на том же уровне связности. Именно в этом случае для моделирования с триангулированными поверхностями [5], [40] стоит использовать методы КЭ с треугольными элементами, или методы КР в сочетании с представлением мозаичных поверхностей [78]. На рисунке 1а представлен пример сложной триангулированной поверхности. Поверхности без информации о связности можно представить с помощью облаков точек рассеяния [39] и неявных представлений поверхности, например функции множеств уровня (level sets function) [106]. Методы с использованием множеств уровня представляют топологию объекта как изоповерхность функции большей размерности. Эти методы хорошо приспособлены для работы вместе с методами частиц, потому что функцию уровня можно напрямую представить в том же наборе вычислительных частиц [22], [42], [99]. Поэтому мы можем обрабатывать системы с произвольно сложной топологией при постоянных вычислительных затратах и моделировать объекты с подвижными и деформирующимися топологиями без ограничения линейной стабильности. На рисунке 1б изображен эндоплазматический ретикулум, который представлен на компьютере в виде функции множеств уровня для того, чтобы смоделировать процессы диффузии на поверхности этого органоида с помощью методов частиц [99].
5. Выводы
Значение пространственно-временных моделей и численного компьютерного моделирования почти во всех областях биологии быстро растёт. Помимо анализа расчётных данных, в который входит обработка изображений, анализ нуклеотидных последовательностей, кодирующих гены и отдельные белки, кластеризация и компьютерное обучение, в современной биологии также используется мощный инструмент — компьютерное моделирование. В «виртуальных экспериментах» (in silico) на компьютере возможно контролировать все переменные и факторы воздействия, что позволяет нам критически анализировать биологические системы, разрабатывать физические модели для компонентов этих систем и разделять сопряжённые процессы, которые нельзя разделить в реальных экспериментах. Более того, пространственно-временное моделирование позволяет работать в масштабах времени и расстояний, недостижимых в экспериментах. Поэтому мы можем изучать системы крошечные, как атомы в молекуле белка, или огромные, как экосистемы целиком.
Особенности биологических систем часто затрудняют разработку и собственно функционирование пространственно-временных моделей. Механизмы регуляции, сложность геометрических форм, нелинейность и взаимодействие на разных уровнях и масштабах — всё это усложняет модели и требует применения мощных и универсальных численных методов, а также эффективных высокопроизводительных программ для суперкомпьютеров [97], [115].
В нашем обзоре мы рассмотрели несколько самых распространённых методов моделирования и классифицировали их согласно следующим параметрам: феноменологичекие—физические, дискретные—непрерывные и детерминистические—стохастические, а также вкратце обсудили возможность применения некоторых численных методов моделирования для каждого класса моделей и дали ссылки на специализированную литературу. Также мы обосновали необходимость использовать для моделирования точечные методы частиц, для которых не требуется никакая основанная на связности дискретизация, и которые пригодны для моделирования как дискретных, так и непрерывных систем. Хотя эти методы стандартно используются для описания дискретных систем, для непрерывных систем они применяютя нечасто. Несмотря на то, что биологические системы изначально сложны, существует большое количество методик и инструментов для создания достоверных пространственно-временных моделей с высокой точностью предсказания. В то же время биология уверенно стимулирует развитие технологий — новых методов и достижений в области численного анализа, науки о вычислениях и высокопроизводительных вычислений.
На передовой вычислительной математики находятся численные методы, эффективно описывающие многомасштабные системы [3], [14], [52], [53], [71] и изменения в сложной топологии объектов. Параллельно с ними должны существовать компьютерные алгоритмы, достаточно эффективные, чтобы работать с большим количеством степеней свободы. Нужны надёжные и эффективные программные продукты для выполнения этих алгоритмов на многопроцессорных суперкомпьютерах [97]. Изучение динамики жидкостей, а именно поиск решений для нелинейной и многомасштабной проблемы описания турбулентности, когда-то запустил развитие численных методов, и такой же скачок может произойти в будущем как результат наших попыток смоделировать клетку целиком [117].
Перевод обзора Иво Сбальцарини [123].
Литература
- Alberts B., Bray D., Johnson A., Lewis J., Raff M., Roberts K., Walter P. Essential Cell Biology. NY: Garland Publication, Inc., 1997;
- Aurélien Alfonsi, Eric Cancès, Gabriel Turinici, Barbara Di Ventura, Wilhelm Huisinga. (2005). Adaptive simulation of hybrid stochastic and deterministic models for biochemical systems. ESAIM: Proc.. 14, 1-13;
- Wolfgang Alt, Mark Chaplain, Michael Griebel, Jürgen Lenz Polymer and Cell Dynamics — Birkhäuser Basel, 2003;
- Miguel A. Aon, Sonia Cortassa. (1994). On the fractal nature of cytoplasm. FEBS Letters. 344, 1-4;
- Eberhard Bänsch, Pedro Morin, Ricardo H. Nochetto. (2005). A finite element method for surface diffusion: the parametric case. Journal of Computational Physics. 203, 321-343;
- Basil Bayati, Philippe Chatelain, Petros Koumoutsakos. (2008). Multiresolution stochastic simulations of reaction–diffusion processes. Phys. Chem. Chem. Phys.. 10, 5963;
- Clément Cancès, Pascal Omnes Finite Volumes for Complex Applications VIII - Hyperbolic, Elliptic and Parabolic Problems — Springer International Publishing, 2017;
- Howard C. Berg Random Walks in Biology — Princeton University Press, 2018;
- Upinder S Bhalla. (2004). Models of cell signaling pathways. Current Opinion in Genetics & Development. 14, 375-381;
- D Bray, R B Bourret, M I Simon. (1993). Computer simulation of the phosphorylation cascade controlling bacterial chemotaxis.. MBoC. 4, 469-482;
- Robert Brown. (1828). XXVII. A brief account of microscopical observations made in the months of June, July and August 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies. The Philosophical Magazine. 4, 161-173;
- Bruno Burlando. (1993). The Fractal Geometry of Evolution. Journal of Theoretical Biology. 163, 161-172;
- M.A.J. Chaplain, M. Ganesh, I.G. Graham. (2001). Spatio-temporal pattern formation on spherical surfaces: numerical simulation and application to solid tumour growth. Journal of Mathematical Biology. 42, 387-423;
- Chauviere A., Preziosi L., Verdier C. Cell Mechanics: From Single Scale-based Models to Multiscale Modeling. Florida: Chapman & Hall/CRC, 2009;
- Jhih-Wei Chu, Gregory A. Voth. (2006). Coarse-Grained Modeling of the Actin Filament Derived from Atomistic-Scale Simulations. Biophysical Journal. 90, 1572-1582;
- Cottet G.-H. and Koumoutsakos P. Vortex Methods — Theory and Practice. NY: Cambridge University Press, 2000;
- Mark J. Dayel, Erik F.Y. Hom, A.S. Verkman. (1999). Diffusion of Green Fluorescent Protein in the Aqueous-Phase Lumen of Endoplasmic Reticulum. Biophysical Journal. 76, 2843-2851;
- Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars Computational Geometry — Springer Berlin Heidelberg, 2008;
- Dimiter S. Dimitrov. (2004). Virus entry: molecular mechanisms and biomedical applications. Nat Rev Microbiol. 2, 109-122;
- Anh-Tuan Dinh, Theo Theofanous, Samir Mitragotri. (2005). A Model for Intracellular Trafficking of Adenoviral Vectors. Biophysical Journal. 89, 1574-1588;
- A. Einstein. (1905). Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys.. 322, 549-560;
- Douglas Enright, Ronald Fedkiw, Joel Ferziger, Ian Mitchell. (2002). A Hybrid Particle Level Set Method for Improved Interface Capturing. Journal of Computational Physics. 183, 83-116;
- Evans G., Blackledge J., Yardley P.. Numerical Methods for Partial Differential Equations. Springer, 1999;
- Christopher P. Fall, Eric S. Marland, John M. Wagner, John J. Tyson Computational Cell Biology — Springer New York, 2004;
- Farlow S.J. Partial Differential Equations for Scientists and Engineers. Dover Publications, 1993;
- Lars Ferm, Andreas Hellander, Per Lötstedt. (2010). An adaptive algorithm for simulation of stochastic reaction–diffusion processes. Journal of Computational Physics. 229, 343-360;
- Understanding Molecular Simulation — Elsevier, 2002;
- Richard J. Gaylord, Kazume Nishidate Modeling Nature — Springer New York, 1996;
- Michael A. Gibson, Jehoshua Bruck. (2000). Efficient Exact Stochastic Simulation of Chemical Systems with Many Species and Many Channels. J. Phys. Chem. A. 104, 1876-1889;
- A. Gierer, H. Meinhardt. (1972). A theory of biological pattern formation. Kybernetik. 12, 30-39;
- Daniel T Gillespie. (1976). A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. Journal of Computational Physics. 22, 403-434;
- Daniel T. Gillespie. (1977). Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem.. 81, 2340-2361;
- González-Segredo N. Amphiphilic fluids: mesoscopicmodel-ling and computer simulations. In: Soft Condensed Matter: New Research. NY: Nova Science, 2007;
- Mark R. Grant, Keith E. Mostov, Thea D. Tlsty, C. Anthony Hunt. (2006). Simulating Properties of In Vitro Epithelial Cell Morphogenesis. PLoS Comp Biol. 2, e129;
- J. GRASMAN, J.W. BRASCAMP, J.L. VAN LEEUWEN, B. VAN PUTTEN. (2003). The Multifractal Structure of Arterial Trees. Journal of Theoretical Biology. 220, 75-82;
- Urs F. Greber, Michael Way. (2006). A Superhighway to Virus Infection. Cell. 124, 741-754;
- H. P. Grimm, A. B. Verkhovsky, A. Mogilner, J.-J. Meister. (2003). Analysis of actin dynamics at the leading edge of crawling cells: implications for the shape of keratocyte lamellipodia. European Biophysics Journal. 32, 563-577;
- Christian Grossmann, Hans-Gorg Roos, Martin Stynes Numerical Treatment of Partial Differential Equations — Springer Berlin Heidelberg, 2007;
- J. Haber, F. Zeilfelder, O. Davydov, H.-P. Seidel. (). Smooth approximation and rendering of large scattered data sets. Proceedings Visualization, 2001. VIS '01.;
- Lionel G. Harrison, Stephan Wehner, David M. Holloway. (2002). Complex morphogenesis of surfaces: theory and experiment on coupling of reaction–diffusion patterning to growth. Faraday Disc.. 120, 277-293;
- Burkhard A. Hense, Christina Kuttler, Johannes Müller, Michael Rothballer, Anton Hartmann, Jan-Ulrich Kreft. (2007). Does efficiency sensing unify diffusion and quorum sensing?. Nat Rev Micro. 5, 230-239;
- Simone E. Hieber, Petros Koumoutsakos. (2005). A Lagrangian particle level set method. Journal of Computational Physics. 210, 342-367;
- Desmond J. Higham.. (2001). An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev.. 43, 525-546;
- Ilachinski A. Cellular Automata. World Scientific Publishing, 2001;
- Samuel A. Isaacson, Charles S. Peskin. (2006). Incorporating Diffusion in Complex Geometries into Stochastic Chemical Kinetics Simulations. SIAM J. Sci. Comput.. 28, 47-74;
- Yi Jiang, Jelena Pjesivac-Grbovic, Charles Cantrell, James P. Freyer. (2005). A Multiscale Model for Avascular Tumor Growth. Biophysical Journal. 89, 3884-3894;
- H. Jonsson, M. Heisler, G. V. Reddy, V. Agrawal, V. Gor, et. al.. (2005). Modeling the organization of the WUSCHEL expression domain in the shoot apical meristem. Bioinformatics. 21, i232-i240;
- Jaap A. Kaandorp, Peter M. A. Sloot, Roeland M. H. Merks, Rolf P. M. Bak, Mark J. A. Vermeij, Cornelia Maier. (2005). Morphogenesis of the branching reef coralMadracis mirabilis. Proceedings of the Royal Society B: Biological Sciences. 272, 127-133;
- Akiko Kashiwagi, Itaru Urabe, Kunihiko Kaneko, Tetsuya Yomo. (2006). Adaptive Response of a Gene Network to Environmental Changes by Fitness-Induced Attractor Selection. PLoS ONE. 1, e49;
- Kincaid D.R. and Ward Cheney E. Numerical Analysis: Mathematics of Scientific Computing. Brooks Cole, 2001;
- Peter E. Kloeden, Eckhard Platen Numerical Solution of Stochastic Differential Equations — Springer Berlin Heidelberg, 1992;
- Petros Koumoutsakos. (2005). MULTISCALE FLOW SIMULATIONS USING PARTICLES. Annu. Rev. Fluid Mech.. 37, 457-487;
- Kovalenko A., Gusarov S., Stepanova M. Multiscale Modeling: Concepts, Theories, and Applications. Florida: CRC Press, 2010;
- Tapobrata Lahiri, Abhijit Chakrabarti, Anjan Kumar Dasgupta. (1998). Multilamellar Vesicular Clusters of Phosphatidylcholine and Their Sensitivity to Spectrin: A Study by Fractal Analysis. Journal of Structural Biology. 123, 179-186;
- Randall J. LeVeque Finite Volume Methods for Hyperbolic Problems — Cambridge University Press, 2002;
- Houqiang Li, Shuhua Chen, Huaming Zhao. (1991). Fat fractal and multifractals for protein and enzyme surfaces. International Journal of Biological Macromolecules. 13, 210-216;
- Houqiang Li, Ying Li, Huaming Zhao. (1990). Fractal analysis of protein chain conformation. International Journal of Biological Macromolecules. 12, 6-8;
- Meshfree Particle Methods — Springer Berlin Heidelberg, 2004;
- Larry S. Liebovitch, Daniela Scheurle, Marian Rusek, Michal Zochowski. (2001). Fractal Methods to Analyze Ion Channel Kinetics. Methods. 24, 359-375;
- K. Lipkow, S. S. Andrews, D. Bray. (2005). Simulated Diffusion of Phosphorylated CheY through the Cytoplasm of Escherichia coli. Journal of Bacteriology. 187, 45-53;
- Jennifer Lippincott-Schwartz, Erik Snapp, Anne Kenworthy. (2001). Studying protein dynamics in living cells. Nat Rev Mol Cell Biol. 2, 444-456;
- An Introduction to Meshfree Methods and Their Programming — Springer-Verlag, 2005;
- Jun S. Liu Monte Carlo Strategies in Scientific Computing — Springer New York, 2004;
- Paul Macklin, John Lowengrub. (2005). Evolving interfaces via gradients of geometry-dependent interior Poisson problems: application to tumor growth. Journal of Computational Physics. 203, 191-220;
- Anotida Madzvamuse, Andrew J. Wathen, Philip K. Maini. (2003). A moving grid finite element method applied to a model biological pattern generator. Journal of Computational Physics. 190, 478-500;
- Tiina Manninen, Marja-Leena Linne, Keijo Ruohonen. (2006). Developing Itô stochastic differential equation models for neuronal signal transduction pathways. Computational Biology and Chemistry. 30, 280-291;
- Eugenio Marco, Roland Wedlich-Soldner, Rong Li, Steven J. Altschuler, Lani F. Wu. (2007). Endocytosis Optimizes the Dynamic Localization of Membrane Proteins that Regulate Cortical Polarity. Cell. 129, 411-422;
- Marée A.F.M. From Pattern Formation to Morphogenesis. PhD thesis. University of Utrecht, 2000;
- Mark Marsh, Ari Helenius. (2006). Virus Entry: Open Sesame. Cell. 124, 729-740;
- Marwan W. (2003). Theory of time-resolved complementation and its use to explore the sporulation control network in Physarum polycephalum. Genetics. 164, 105–115;
- Alexander Mielke Analysis, Modeling and Simulation of Multiscale Problems — Springer Berlin Heidelberg, 2006;
- F Milinazzo, P.G Saffman. (1977). The calculation of large reynolds number two-dimensional flow using discrete vortices with random walk. Journal of Computational Physics. 23, 380-392;
- T MIURA. (2004). Speed of pattern appearance in reaction-diffusion models: implications in the pattern formation of limb bud mesenchyme cells. Bulletin of Mathematical Biology. 66, 627-649;
- Hans-Joachim Mosler, Karsten Schwarz, Florin Ammann, Heinz Gutscher. (2001). Computer Simulation as a Method of Further Developing a Theory: Simulating the Elaboration Likelihood Model. Pers Soc Psychol Rev. 5, 201-215;
- Johannes Müller, Christina Kuttler, Burkard A. Hense, Michael Rothballer, Anton Hartmann. (2006). Cell–cell communication by quorum sensing and dimension-reduction. J. Math. Biol.. 53, 672-702;
- Nadler Jr.S.B. Continuum Theory. Basel and Hong Kong: M. Dekker, 1992;
- T.J. Newman, J. Antonovics, H.M. Wilbur. (2002). Population Dynamics with a Refuge: Fractal Basins and the Suppression of Chaos. Theoretical Population Biology. 62, 121-128;
- Igor L. Novak, Fei Gao, Yung-Sze Choi, Diana Resasco, James C. Schaff, Boris M. Slepchenko. (2007). Diffusion on a curved surface coupled to diffusion in the volume: Application to cell biology. Journal of Computational Physics. 226, 1271-1290;
- Oksendal B.K. Stochastic Differential Equations. Springer, 2003;
- Xavier Periole, Thomas Huber, Siewert-Jan Marrink, Thomas P. Sakmar. (2007). G Protein-Coupled Receptors Self-Assemble in Dynamics Simulations of Model Bilayers. J. Am. Chem. Soc.. 129, 10126-10132;
- Plimpton S.J. and Slepoy A. (2005). Microbial cell modeling via reacting diffusive particles. J. Phys. 16, 305–309;
- Anton A. Polyansky, Rajesh Ramaswamy, Pavel E. Volynsky, Ivo F. Sbalzarini, Siewert J. Marrink, Roman G. Efremov. (2010). Antimicrobial Peptides Induce Growth of Phosphatidylglycerol Domains in a Model Bacterial Membrane. J. Phys. Chem. Lett.. 1, 3108-3111;
- Rajesh Ramaswamy, Nélido González-Segredo, Ivo F. Sbalzarini. (2009). A new class of highly efficient exact stochastic simulation algorithms for chemical reaction networks. The Journal of Chemical Physics. 130, 244104;
- Rajesh Ramaswamy, Ivo F. Sbalzarini, Theodore E. Simos, George Psihoyios, Ch. Tsitouras. (2010). Fast Exact Stochastic Simulation Algorithms Using Partial Propensities. ;
- Rajesh Ramaswamy, Ivo F. Sbalzarini. (2010). A partial-propensity variant of the composition-rejection stochastic simulation algorithm for chemical reaction networks. The Journal of Chemical Physics. 132, 044102;
- Erik M Rauch, Mark M Millonas. (2004). The role of trans-membrane signal transduction in turing-type cellular pattern formation. Journal of Theoretical Biology. 226, 401-407;
- Reddy J.N. Finite Element Method. McGraw-Hill, 1993;
- Benedict J. Reynwar, Gregoria Illya, Vagelis A. Harmandaris, Martin M. Müller, Kurt Kremer, Markus Deserno. (2007). Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature. 447, 461-464;
- Jason Riordan, Charles R. Doering, Daniel ben-Avraham. (1995). Fluctuations and Stability of Fisher Waves. Phys. Rev. Lett.. 75, 565-568;
- Diego Rossinelli, Basil Bayati, Petros Koumoutsakos. (2008). Accelerated stochastic and hybrid methods for spatial simulations of reaction–diffusion systems. Chemical Physics Letters. 451, 136-140;
- Reuven Y. Rubinstein, Dirk P. Kroese Simulation and the Monte Carlo Method — John Wiley & Sons, Inc., 2016;
- Antti Saarinen, Marja-Leena Linne, Olli Yli-Harja. (2008). Stochastic Differential Equation Model for Cerebellar Granule Cell Excitability. PLoS Comput Biol. 4, e1000004;
- Howard Salis, Vassilios Sotiropoulos, YiannisN Kaznessis. (2006). . BMC Bioinformatics. 7, 93;
- M.J. Saxton. (1994). Anomalous diffusion due to obstacles: a Monte Carlo study. Biophysical Journal. 66, 394-401;
- Michael J. Saxton. (2001). Anomalous Subdiffusion in Fluorescence Photobleaching Recovery: A Monte Carlo Study. Biophysical Journal. 81, 2226-2240;
- Michael J. Saxton. (2007). A Biological Interpretation of Transient Anomalous Subdiffusion. I. Qualitative Model. Biophysical Journal. 92, 1178-1191;
- I.F. Sbalzarini, J.H. Walther, M. Bergdorf, S.E. Hieber, E.M. Kotsalis, P. Koumoutsakos. (2006). PPM – A highly efficient parallel particle–mesh library for the simulation of continuum systems. Journal of Computational Physics. 215, 566-588;
- Sbalzarini I.F. Analysis, Modeling & Simulation of Diffusion Processes in Cell Biology. VDM Publishing, 2009;
- Ivo F. Sbalzarini, Arnold Hayer, Ari Helenius, Petros Koumoutsakos. (2006). Simulations of (An)Isotropic Diffusion on Curved Biological Surfaces. Biophysical Journal. 90, 878-885;
- Ivo F. Sbalzarini, Anna Mezzacasa, Ari Helenius, Petros Koumoutsakos. (2005). Effects of Organelle Shape on Fluorescence Recovery after Photobleaching. Biophysical Journal. 89, 1482-1492;
- Schiff J.L. Cellular Automata: A Discrete View of the World. Wiley Interscience, 2008;
- Birte Schrader, Sylvain Reboux, Ivo F. Sbalzarini. (2010). Discretization correction of general integral PSE Operators for particle methods. Journal of Computational Physics. 229, 4159-4182;
- Schrödinger E. What is Life? The Physical Aspect of the Living Cell. Cambridge University Press, 1948;
- Schumaker L.L. Triangulation methods. In: Multivariate Approximation. Academic Press, 1987. — P. 219–232;
- Schweitzer F. Brownian Agents and Active Particles. On the Emergence of Complex Behavior in the Natural and Social Sciences. Springer, 2003;
- Sethian J.A. Level Set Methods and Fast Marching Methods. Cambridge, UK: Cambridge University Press, 1999;
- Boris M. Slepchenko, James C. Schaff, John H. Carson, Leslie M. Loew. (2002). Computational Cell Biology: Spatiotemporal Simulation of Cellular Events. Annu. Rev. Biophys. Biomol. Struct.. 31, 423-441;
- Alexander Slepoy, Aidan P. Thompson, Steven J. Plimpton. (2008). A constant-time kinetic Monte Carlo algorithm for simulation of large biochemical reaction networks. The Journal of Chemical Physics. 128, 205101;
- A. E. Smith. (2004). How Viruses Enter Animal Cells. Science. 304, 237-242;
- Smith G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods. Oxford, 1985;
- T.G. Smith, W.B. Marks, G.D. Lange, W.H. Sheriff, E.A. Neale. (1989). A fractal analysis of cell images. Journal of Neuroscience Methods. 27, 173-180;
- Strauss W.A. Partial Differential Equations: An Introduction. Wiley, 2007;
- Strogatz S.H. Nonlinear Dynamics and Chaos. Westview Press, 2000;
- Audrius B. Stundzia, Charles J. Lumsden. (1996). Stochastic Simulation of Coupled Reaction–Diffusion Processes. Journal of Computational Physics. 127, 196-207;
- K. Takahashi, K. Yugi, K. Hashimoto, Y. Yamada, C.J.F. Pickett, M. Tomita. (2002). Computational challenges in cell simulation: a software engineering approach. IEEE Intell. Syst.. 17, 64-71;
- Takao Terano, Hajime Kita, Toshiyuki Kaneda, Kiyoshi Arai, Hiroshi Deguchi Agent-Based Simulation: From Modeling Methodologies to Real-World Applications — Springer-Verlag, 2005;
- The 2020 Science Group. Towards 2020 Science. (2005). Microsoft;
- . (1952). The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B. 237, 37-72;
- Greg Turk. (1991). Generating textures on arbitrary surfaces using reaction-diffusion. Proceedings of the 18th annual conference on Computer graphics and interactive techniques - SIGGRAPH '91;
- Alan S Verkman. (2002). Solute and macromolecule diffusion in cellular aqueous compartments. Trends in Biochemical Sciences. 27, 27-33;
- Zienkiewicz O.C. and Taylor R.L. The Finite Element Method. Butterworth-Heinemann, 2005;
- Молекулярная динамика биомолекул. Часть I. История полувековой давности;
- Ivo F. Sbalzarini. (2009). Spatiotemporal Modeling and Simulation in Biology. Bioinformatics. 381-432.