Физическая водобоязнь
16 января 2013
Физическая водобоязнь
- 10126
- 5
- 11
Степень гидрофобности материала можно определять по углу смачивания, от которого зависит, будет ли вода растекаться по поверхности или собираться в капельки
-
Авторы
-
Редакторы
Лист лотоса, по которому вода бегает, собравшись в шарики, водоотталкивающие поверхности и защитные составы для обуви, плавающие в бульоне кружки масла — всё это примеры свойства молекул, называемого гидрофобностью. Помимо этого, гидрофобный эффект играет важную биологическую роль: сворачивание и правильная работа белковых молекул, формирование биомембран, распознавание молекулами друг друга также «запрограммированы» с использованием гидрофобных свойств. Интересно, что гидрофобный эффект не сводится к «обычным» физическим взаимодействиям: за ним стоит Второй закон термодинамики и величина, именуемая энтропией.
Знакомое всем с детства выражение «как с гуся вода» показывает, что гидрофобность — не такое уж невиданное явление, как можно подумать по его названию. Действительно, эффект «отталкивания» воды часто встречается вокруг нас: достаточно посмотреть на гусиное перо или лист лотоса (рис. 1а), по которым капелька воды сбегает, подобно шарику ртути по поверхности стекла, не оставляя за собой никакого следа. Классические представления о гидрофобных поверхностях говорят, что показателем тут является краевой угол смачивания θ, который для смачиваемых поверхностей меньше прямого угла (90°), а для несмачиваемых — больше него (рис. 1б) [1]. В частности, для капельки воды на поверхности парафина θ = 109°, а на поверхности самого гидрофобного известного материала — фторопласта — это будет 112°. В то же время, «абсолютно» гидрофобная поверхность описывалась бы углом 180°, когда вода скатывается с поверхности, ни секунды на ней не задерживаясь.
...Так неужели гусь гидрофобнее фторопласта? Фактически так и есть, но достигается это за счет небольшой уловки: поверхность пера гуся (равно как и листа лотоса) не ровная, а покрытая микроскопическими пирамидками или волосками, что уменьшает площадь контакта с каплей и эффективную адгезию (рис. 1в) [1]. На этом же принципе основаны супергидрофобные поверхности, отталкивающие воду практически идеально (видео 1).
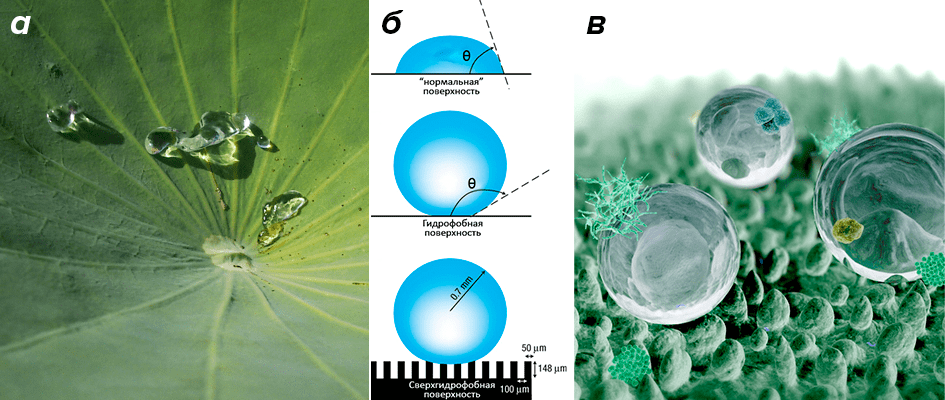
Рисунок 1. Лист лотоса: пример гидрофобной поверхности. а — Гидрофобность фактически означает несмачиваемость, когда вода скатывается с поверхности полностью, не оставляя влажных следов. б — Определение гидрофобной поверхности на основе краевого угла смачивания θ: при θ < 90° поверхность называют смачиваемой (гидрофильной), при θ > 90° — несмачиваемой (гидрофобной). Эффект абсолютной гидрофобности (или супергидрофобности) достигается за счет микроскопических шероховатостей, уменьшающих площадь контакта капли с поверхностью [2]. в — Как устроена поверхность лотоса: микроскопические шипики не дают каплям воды смочить поверхность, и они скатываются с листа. «Затечь» между шипиками капля воды тоже не может, потому что в этом масштабе поверхностное натяжение уже не дает капле дробиться на более мелкие.
Видео 1. Супергидрофобная поверхность. Микромасштабная шероховатость поверхности (см. рис. 1б) снижает эффективную площадь контакта с каплей воды, которая в этом масштабе за счет поверхностного натяжения ведет себя подобно упругому телу.
Чтобы понять, почему одни вещества с удовольствием смачиваются водой, а с гуся она, как гласит пословица, скатывается, нужно опуститься на уровень отдельных молекул и рассмотреть, как молекулы взаимодействуют между собой.
Гидрофобные молекулы
С точки зрения химического строения гидрофобными (или, что то же самое, неполярными) являются молекулы, не содержащие химических групп, способных образовывать с водой водородные связи. Например, это бензол и другие жидкие углеводороды (составляющие бензина). Однако наиболее интересными свойствами обладают амфифильные молекулы, содержащие как полярную, так и неполярную части: это приводит к тому, что они образуют в смесях с водой довольно сложные структуры: мицеллы, везикулы, слои и более сложные формы. Образование всех этих сложных форм управляется гидрофобным эффектом.
Что интересно, вопрос о молекулярной природе гидрофобности восходит еще к Бенджамину Франклину, который в свободное от государственных дел время исследовал растекание оливкового масла по поверхности пруда [3], [4]. Площадь пятна от одной ложки масла получалась все время одна и та же — пол-акра, — а толщина фактически равнялась одной молекуле. Дело было в 1774 году, и хотя тогда представления о молекулярной природе веществ были еще крайне туманны, общая любознательность государственных мужей была, как видим, не в пример нынешней. Так или иначе, эксперимент с маслом положил начало исследованиям мономолекулярных липидных пленок, из которых несомненно стало ясно: некоторые молекулы настолько «не любят» воду, что не только не смешиваются с ней, но и готовы устраняться от воды всеми возможными способами — например, скапливаясь в виде слоя толщиной в одну молекулу (монослоя) на границе воды с воздухом. (Подробнее с исследованиями липидных пленок можно ознакомиться в статье «Молекулы-русалки» [4].)
Другим важным типом молекул-амфифилов являются мылá, повсеместно применяемые в быту и в народном хозяйстве [5]. Принцип их действия можно подчерпнуть даже из рекламных роликов: неполярная часть молекул моющего средства «слипается» с молекулами загрязнителя (как правило, гидрофобными), а полярная часть активно взаимодействует с молекулами воды. В результате происходит солюбилизация: грязь отрывается от поверхности и заключается внутрь агрегирующих молекул мыла, выставляющих полярные фрагменты «наружу» и прячущих гидрофобные части «внутрь» [5].
Однако наслаждаться товарными качествами лучших моющих средств позволяет нам еще более важное качество амфифильных молекул (а именно, липидов): они служат оболочкой для всех известных форм жизни, образуя мембрану клеток, под которой протекают все жизненные процессы (см. «Липидный фундамент жизни» [3]). Этот немаловажный факт говорит нам, что молекулярная природа гидрофобного эффекта — вещь отнюдь не праздная, но имеющая фундаментальное значение для всей биологии, не говоря уже о прикладных отраслях.
Но при ближайшем рассмотрении оказывается, что за «притяжение» гидрофобных частиц друг к другу и «отталкивание» их от воды не отвечает никакое фундаментальное физическое взаимодействие, вроде гравитации или электростатических сил. Его природа кроется в физическом принципе, накладывающем ограничение на направление протекания большинства спонтанных процессов, — а именно, во Втором начале термодинамики.
Немного термодинамики
Термодинамика — одна из первых наук, перебросивших мостки между микроскопическим миром атомов и молекул и «нашим», макроскопическим миром. Ее рождение связывается с изучением работы паровых машин и именем Николá Карно (1796–1832), в честь которого названы термодинамические циклы, определяющие количество работы, которое может произвести машина. Его дело продолжили Джоуль, Кельвин и Клаузиус, которые подвели под эту первоначально сугубо практическую область мощную теоретическую базу.
Усилиями этих ученых сформулированы основные законы, или начала, термодинамики, обобщающие многовековой эмпирический опыт наблюдения за тепловыми процессами. Первое начало говорит о сохранности энергии изолированной системы («закон сохранения энергии»), а второе — о направлении протекания самопроизвольных процессов. (Еще есть нулевое и третье начала, но здесь мы о них говорить не будем.) Со Вторым началом неразрывно связано понятие энтропии (S), которая снискала славу самой загадочной термодинамической величины. Первоначально формально определенная Клаузиусом как отношение сообщаемого системе тепла к температуре (ΔS = ΔQ/T), позже энтропия обрела смысл глобальной «меры хаоса». С тех пор энтропия стала основой современной формулировки Второго начала:
Людвиг Больцман (1844–1906) связал всю эту тепловую «кухню» с уровнем составляющих вещество атомов, причем еще до того, как атомарное строение материи стало общепризнанным. Главным достижением своей жизни он считал открытие (в 1877 году) статистической формулы для исчисления энтропии: S = k × logW, где S — это энтропия, k — константа, названная позднее Планком именем самого Больцмана, а W — статистический вес состояния (число микросостояний, которым реализуется данное макросостояние). Несмотря на плохое зрение, он видел существенно глубже остальных «вглубь» материи: он первым почувствовал мощь статистического подхода к описанию термодинамических ансамблей и применил его в молекулярной физике. Существует версия, что Больцман покончил с собой из-за непонимания современников, которых он кардинальным образом опередил. Упомянутая выше формула высечена на его надгробии на кладбище в Вене.
Несмотря на всю таинственность понятия энтропии, смысл Второго закона достаточно прост: если система изолирована (то есть, не обменивается с внешним миром ни веществом, ни энергией), то она будет стремиться к состоянию термодинамического равновесия, — такому макросостоянию, которое реализуется максимально возможным числом микросостояний (другими словами, которое имеет максимальную энтропию). К примеру, разбившаяся чашка никогда вновь не склеится сама: начальное состояние (целая чашка) реализуется лишь одним способом (S=0), а вот конечное (расколотая чашка) — астрономически большим числом способов (S>>0). Поэтому, увы, в глобальной перспективе все чашки обречены. Объяснению Второго закона «для домохозяек» посвящена замечательная научно-популярная книга Питера Эткинса «Порядок и беспорядок в природе» [6].
Гидрофобный эффект с точки зрения статистической физики
Итак, зная Второй закон, мы понимаем, почему чашка чая на столе обязательно остынет до комнатной температуры, но никогда сама по себе не нагреется вновь, отобрав тепло у воздуха в кухне. (Если нет — то надо обязательно прочитать книгу Эткинса [6].) Но применимы ли те же самые рассуждения для объяснения, например, несмешиваемости воды и масла? Ведь Второй закон стремится «все уровнять», а вода с маслом, наоборот, отказываются растворяться друг в друге (рис. 2а).
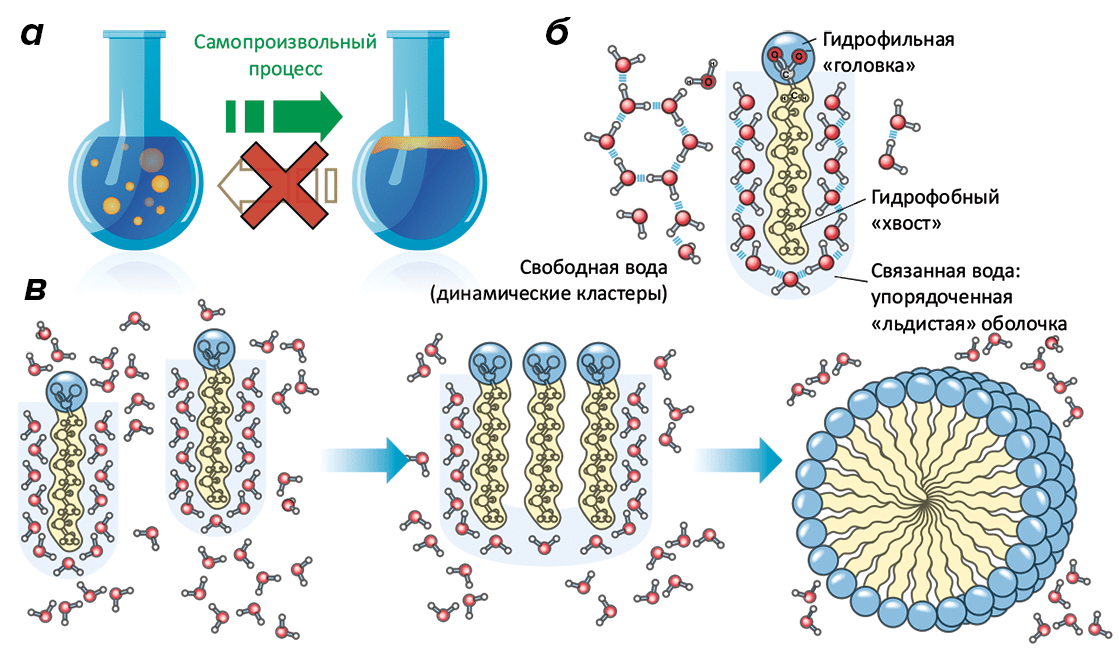
Рисунок 2. Иллюстрация гидрофобного эффекта. а — Гидрофобный эффект (а по сути, Второй закон термодинамики) заставляет воду «отталкивать» неполярные молекулы (такие как масло) и уменьшать площадь контакта с ними. Из-за этого много маленьких капелек масла в воде в конечном итоге обязательно сольются вместе и образуют слой. б — Образование упорядоченного («льдистого») слоя молекул воды вблизи гидрофобной поверхности необходимо, чтобы молекулы воды могли формировать водородные связи друг с другом. Но это приводит к падению энтропии, невыгодному в связи со Вторым законом. в — Естественная возможность увеличить энтропию — снизить площадь контакта гидрофобных молекул с водой, что и происходит при агрегации нескольких неполярных молекул между собой. В случае амфифильных молекул появляется самоорганизация и формирование довольно сложных надмолекулярных структур, таких как мицеллы, бислои и везикулы (см. рис. 3).
[7] (б и в)
И впрямь, если рассматривать только масло, то покажется, что термодинамика не работает: растворение масляной пленки в толще жидкости явно увеличило бы энтропию по сравнению с монослоем. Но все знают, что на самом-то деле происходит все наоборот: даже если воду с маслом встряхнуть, эмульсия через какое-то время распадется, и масло опять образует пленку, покинув водную фазу.
Дело в том, что вода в этом примере — равноправный участник рассматриваемой системы, и ее ни в коем случае нельзя упускать из виду. Как известно, свойства воды (даже ее жидкое состояние в нормальных условиях) обусловлены способностью образовывать водородные связи. Каждая молекула воды может формировать до четырех связей с «соседками», но для этого вода должна находиться «в воде». В случае присутствия в воде неполярной поверхности, примыкающие к ней молекулы перестают чувствовать себя «свободно»: для того, чтобы сформировать желаемые водородные связи, этим молекулам приходится ориентироваться строго определенным образом, формируя «льдистую» оболочку (рис. 2б) вокруг гидрофобного объекта. Это вынужденное упорядочивание характерно существенным падением энтропии системы масло—вода, что и вынуждает гидрофобные молекулы агрегировать между собой, уменьшая площадь контакта с полярной средой, а значит, и невыгодное снижение энтропийного фактора [8]. Фактически, это вода заставляет масло сливаться в одну большую каплю или пятно, реализуя диалектический принцип «подобное к подобному».
Такое взаимодействие полярной и неполярной фаз носит название гидрофобного эффекта. Это явление заставляет молекулы детергентов образовывать в растворе мицеллы, липиды — формировать моно- и бислои. Последние могут замыкаться на себя с образованием пузырьков (липосом) или биологических мембран, окружающих клетку (рис. 3). Найдены и более сложные формы липидного полиморфизма, например кубическая липидная фаза, широко используемая в структурных исследованиях мембранных белков.
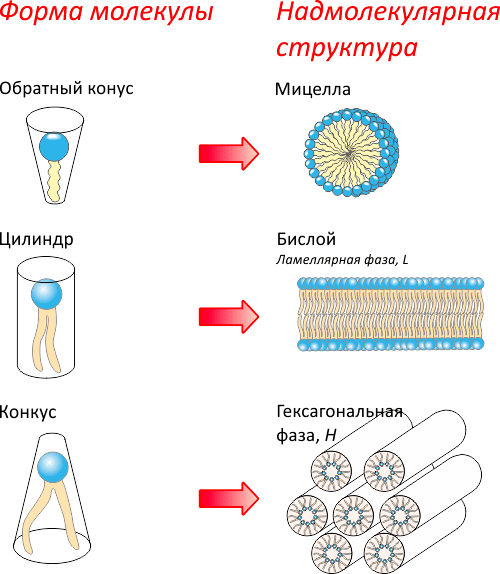
Рисунок 3. Липидный полиморфизм. В зависимости от формы и других свойств молекулы, характеризующих несимметричное строение головки и хвоста, липиды образуют различные надмолекулярные структуры. Сверху вниз: 1 — при обратной конической форме молекулы образуются структуры с положительной кривизной (мицеллы и гексагональная фаза HI); 2 — цилиндрическая форма дает плоские (ламеллярные) структуры, такие как бислои; 3 — при конической форме образуются кубическая фаза и обращенные гексагональная (HII) и мицеллярная фазы.
«Вглубь» гидрофобного эффекта
В случае биологических молекул гидрофобный эффект играет особую роль, поскольку он формирует биомембраны, без которых невозможна жизнь [3], а также вносит определяющий (до 90% всей работы) вклад в сворачивание белковых молекул, боковые цепи аминокислотных остатков которых могут иметь различную природу: гидрофобную или гидрофильную. Наличие столь разных сущностей в пределах одной линейной молекулы дает все разнообразие форм и выполняемых функций, которое наблюдается у белков.
Однако в субмолекулярных масштабах гидрофобный эффект проявляется иначе, нежели в случае протяженной неполярной поверхности или целой ложки масла: по-видимому, кластер гидрофобных частиц будет стабильным, только если его размер превышает пороговое значение (≈1 нм); иначе он будет разрушен тепловым движением молекул [9]. Моделирование молекулярной динамики (МД [10]) показывает различие в структуре «чистой» воды и воды вблизи маленькой (<1 нм) и большой (>>1 нм) гидрофобных частиц. Если в первых двух случаях каждая молекула воды может образовывать до четырех водородных связей, то в случае крупной гидрофобной частицы такая возможность отсутствует, и молекулам воды приходится выстраиваться в «льдистую» оболочку вокруг этой частицы (рисунки 2б и 4).
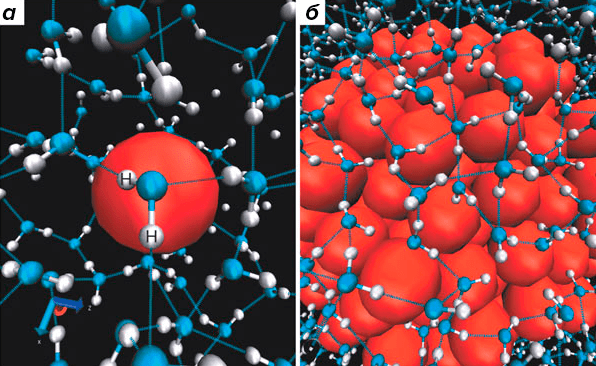
Рисунок 4. Различная конфигурация молекул воды вблизи маленькой (а) и большой (б) гидрофобных частиц (в обоих случаях изображены красными сферами). Согласно данным МД, частицы размером менее 1 нм могут быть легко окружены водой без ограничения ее «свободы» и способности образования водородных связей. В случае более крупных частиц, чтобы образовать водородную связь, пограничной молекуле воды приходится особым образом ориентироваться относительно гидрофобной поверхности, что приводит к упорядочиванию целого водяного слоя (или нескольких) и снижению энтропии растворителя. При этом среднее число водородных связей на молекулу воды уменьшается до трех. Интересно, что здесь меняется и характер зависимости энергии сольватации частицы от ее размера: до 1 нм энергия зависит от объема частицы, а выше этого порога — от площади ее поверхности.
Этот же «пороговый размер» был подтвержден и в эксперименте по определению вклада гидрофобного эффекта в сворачивание полимерной цепочки в зависимости от размера боковой группы мономера и температуры. Регистрация свободной энергии сольватации осуществлялась с помощью атомно-силового микроскопа, «расплетавшего» полимерную молекулу по одному звену за шаг [11]. Интересно, что пограничное значение 1 нм примерно совпадает с размером крупных боковых цепей аминокислотных остатков, определяющих фолдинг молекулы белка.
Поскольку гидрофобный эффект носит энтропийный характер, его роль в различных процессах (то есть, вклад в свободную энергию) зависит от температуры. Любопытно, что этот вклад максимален именно в нормальных условиях — при тех же температуре и давлении, при которых в основном существует жизнь. (В этих же условиях и основной биологический растворитель — вода — находится вблизи равновесия между жидкостью и паром.) Это подталкивает к мысли, что жизнь намеренно «выбирает» условия существования, близкие к фазовым переходам и точкам равновесия: видимо, это обеспечивает возможность особенно надежного контроля и тонкого управления такими, казалось бы, «инертными» вещами, как структура мембран и белковых молекул.
Исследования последних лет еще сильнее подчеркивают роль воды как в гидрофобном эффекте, так и в межмолекулярном распознавании (например, при связывании ферментом своего субстрата или рецептором — распознаваемого им лиганда) [12]. В активном центре белка, как правило, присутствуют «связанные» (а значит, упорядоченные) молекулы воды. При проникновении лиганда в сайт связывания на поверхности белка вода «освобождается», что дает положительный вклад в энтропию (рис. 5); однако энтальпийная компонента изменения свободной энергии может быть как отрицательной, так и положительной . С помощью калориметрического титрования и молекулярного моделирования была установлена термодинамическая картина связывания ферментом карбоангидразой множества лигандов, сходных по структуре, но отличающихся по размеру гидрофобных групп [13]. Анализ показал, что вклад энтальпии и энтропии в свободную энергию Гиббса в каждом случае может быть индивидуальным, и заранее невозможно сказать, какой процесс будет играть решающую роль. Абсолютно точно понятно лишь, что структура и динамика ближайших к активному сайту слоев молекул воды играет в межмолекулярном распознавании такую же важную роль, как и соответствие лиганда рецептору, что привносит новый уровень сложности в «классические» модели взаимодействия двух молекул типа «ключ—замок» или «рука—перчатка».
Изменение свободной энергии Гиббса, являющейся основной движущей силой химических процессов, вычисляют по уравнению ΔG = ΔH − TΔS. Отрицательный знак ΔG говорит о том, что самопроизвольное протекание реакции «разрешено» с термодинамической точки зрения. Как видно из формулы, возможно два пути реализации самопроизвольных процессов: с падением энтальпии или возрастанием энтропии.
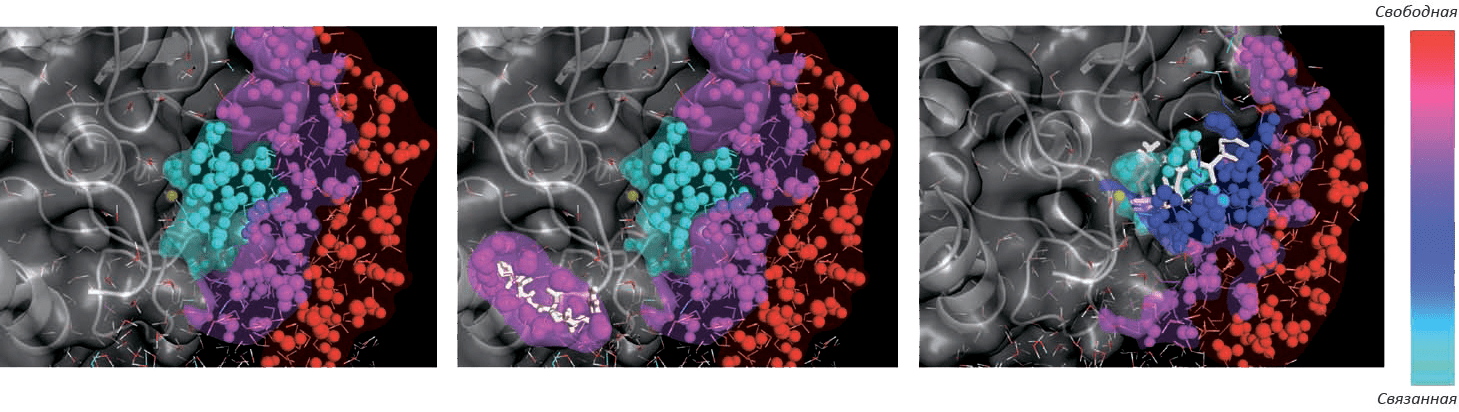
Рисунок 5. Динамика ближайших слоев растворителя играет важную роль во взаимодействии фермент—субстрат. Пример цинковой металлопротеиназы (фермент показан серым, ион цинка — желтым), ее субстрата и растворителя (подвижность молекулы воды изображена цветом). Слева: динамика свободного фермента показывает наличие в активном сайте «связанной» воды. В центре: субстрат на ранних стадиях взаимодействия с ферментом (когда он еще не занимает сайт связывания) уже создает собственную сферу связанной воды. Справа: специфическое взаимодействие фермент—субстрат образует характерную картину подвижности молекул растворителя.
Роль гидрофобного эффекта в фолдинге белка
Фолдингом (сворачиванием) белка называют процесс обретения полипептидной цепью присущей ей трехмерной конформации (нативной формы). Общепринятые представления о физике белка говорят, что нативная конформация обладает наименьшей свободной энергией среди потенциально возможных, благодаря чему этот процесс является самопроизвольным. Несмотря на то, что фолдинг направляется совокупностью, вроде бы, хорошо изученных физических законов, промоделировать его на компьютере пока что в общем случае невозможно . Не в последнюю очередь — благодаря гидрофобному эффекту, который играет в процессе сворачивания цепочки решающую роль, но при этом не сводится к суммированию парных взаимодействий, на чем основаны современные методы эмпирических силовых полей [10], [15].
Более подробно об этом рассказывается в статье «Торжество компьютерных методов: предсказание строения белков» [15].
Сворачивание гомо- и гетерополимеров можно разделить на несколько стадий (рис. 6):
- Если начинать с вытянутой цепочки, первой стадией будет энтропийное сворачивание, являющееся прямым следствием Второго закона термодинамики: полностью распрямленная полипептидная цепь имеет нулевую энтропию, что мгновенно «исправляется» статистическими силами, превращающими нить в «статистический клубок».
- В конформации статистического клубка гидрофобные боковые остатки оказываются сближены в пространстве и агрегируют под влиянием гидрофобного эффекта. Это подтверждено наблюдением за принципами трехмерной упаковки белковых глобул: внутри находится «ядро» из гидрофобных остатков, а на поверхности молекулы располагаются полярные и заряженные аминокислотные остатки. Получающуюся на этой стадии форму называют расплавленной глобулой.
- В случае биополимеров этим дело не кончается: специфические взаимодействия между сближенными в пространстве остатками делают упаковку еще более плотной (истинная глобула). Свободная энергия при этом испытывает существенное падение, и это часто считают критерием «хорошо упакованной» структуры.
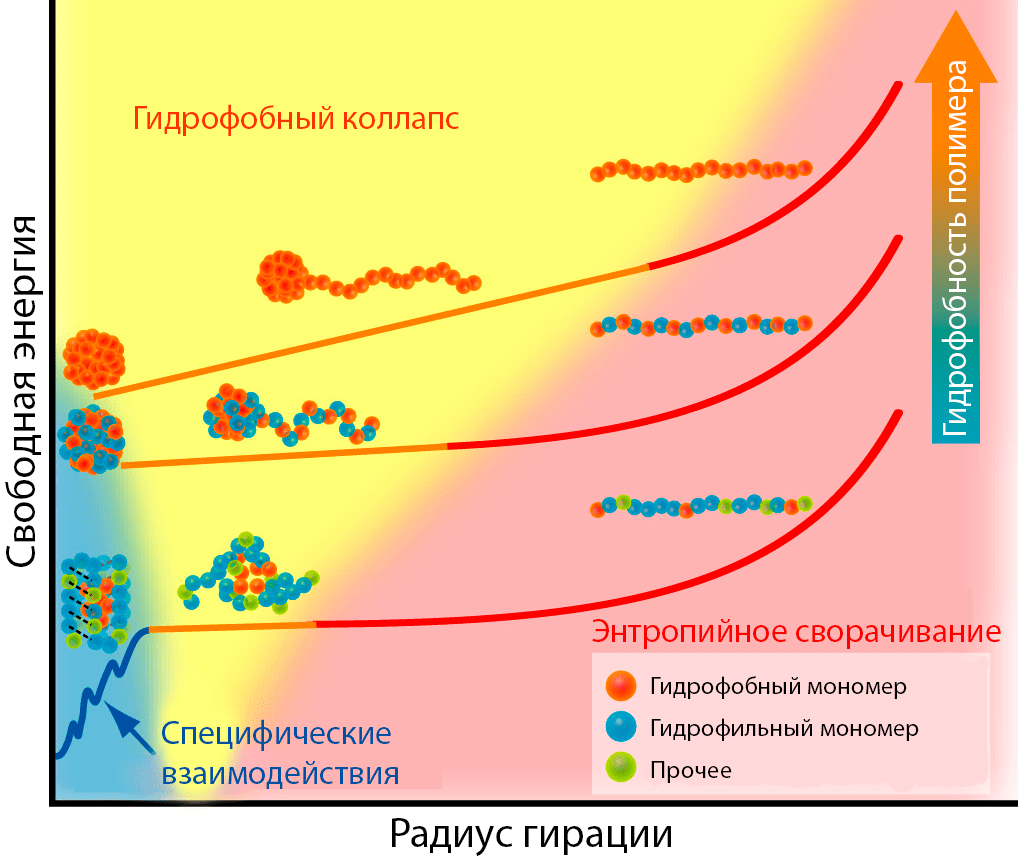
Рисунок 6. Роль гидрофобного коллапса в сворачивании трех полимерных цепей с различной гидрофобностью составляющих мономеров: гидрофобного полимера, гидрофобно-гидрофильного сополимера и глобулярного белка (сверху вниз) — отложена свободная энергия в зависимости от радиуса гирации, показывающего компактность упаковки цепи. 1) Любая линейная цепочка из полностью растянутого состояние быстро скручивается в статистический клубок. 2) Пространственная близость неполярных боковых цепей приводит к гидрофобному коллапсу клубка и образованию расплавленной глобулы. 3) В случае белков эволюционно подобранные специфические контакты между боковыми цепями сближенных аминокислотных остатков (такие как водородные связи или электростатические взаимодействия) дополнительно снижают свободную энергию и упаковывают белок до плотной глобулы. Гидрофобные полимеры не имеют таких взаимодействий, и поэтому их сворачивание останавливается на стадии статистического клубка.
Раньше считалось, что третья стадия является непременным признаком функционального белка, однако в последнее время все больше внимания уделяется так называемым недоупорядоченным белкам (intrinsically disordered proteins), у которых отсутствует четко заданная пространственная форма, и фактически нету стадии образования специфических контактов. (Кстати, доля гидрофобных остатков в них существенно меньше по сравнению с глобулярными белками.) Возможно, это позволяет им взаимодействовать в живой клетке не с одним белком или лигандом, а с десятками или даже сотнями структурно различных молекул-партнеров, принимая участие в весьма тонкой регуляции клеточных процессов [16], [17].
Определяющую роль гидрофобный эффект играет и в фолдинге мембранных белков (МБ), исполняющих множество жизненно-важных функций от транспорта молекул и ионов через мембрану до рецепции и распознавания клетками друг друга. В связи с тем, что бóльшая их часть погружена в гидрофобный бислой мембраны, строение трансмембранного (ТМ) домена существенно отличается от упаковки растворимых глобулярных белков: ТМ-сегменты у них существенно гидрофобнее, причем гидрофобные боковые цепи находятся не только внутри белка (как в случае глобулярных белков), но и на поверхности, где белок контактирует с углеводородными цепями липидных молекул.
Важно, что гидрофобность вступает в дело еще до того, как белок окажется на своем рабочем месте (то есть, в мембране). МБ в процессе рибосомального синтеза попадают не в цитоплазму, как глобулярные белки, а в транслокон — довольно сложную молекулярную машину, построенную в виде канала и отвечающую сразу и за секрецию белков, и за доставку МБ внутрь мембран. Оказалось, что транслокон может «чувствовать» гидрофобность пропускаемого через него фрагмента белка и, при достижении некоторого порога гидрофобности, «выплевывает» этот фрагмент не «вперед» (через канал во внеклеточное пространство), а «вбок» (через стенку канала) — прямо в мембрану. Так, фрагмент за фрагментом, мембранные белки встраиваются в мембрану, и поэтому N-конец у МБ всегда находится во внеклеточной области, а где будет C-конец — зависит от количества ТМ-сегментов.
В изящном эксперименте на транслоконе Sec61 эндоплазматического ретикулума была установлена «биологическая шкала гидрофобности», которая ставит каждому аминокислотному остатку в соответствие определенное значение гидрофобности [18]. Что интересно, в общих чертах эта шкала совпадает с ранее установленными физико-химическими шкалами, что позволяет транслокону приписать роль сенсора гидрофобного взаимодействия.
Итак, клетка может «измерять» гидрофобность с помощью транслокона, а в лаборатории это свойство можно грубо оценить по характеру взаимодействия с водой. Но можно ли гидрофобность рассчитать теоретически и включить этот расчет в практически важные задачи?
Как рассчитать гидрофобность теоретически?
Выше уже было сказано, что гидрофобный эффект есть фактически одно из лиц Второго начала термодинамики, так что рассчитать его аккуратно, пожалуй, ничуть не легче, чем смоделировать всю систему целиком, причем на физически корректном уровне. Другими словами, «гидрофобные взаимодействия» ни в какой мере не сводятся к парным контактам, таким как притяжение или отталкивание двух зарядов или взаимодействие между донором и акцептором водородной связи. Единственный теоретически верный путь — анализ огромного числа микросостояний в термодинамических ансамблях, что на практике сделать довольно сложно.
Однако хотя бы примерная оценка гидрофобных и гидрофильных свойств молекул все же востребована в молекулярном моделировании и его приложениях (например, биотехнологических или индустриальных). Обычно здесь ориентируются на характеристику, описывающую гидрофобность молекулы целиком — коэффициент распределения (P, от partitioning) этого вещества между водой (полярной фазой) и неполярной фазой (например, бензолом или н-октанолом). Дело в том, что этот параметр, в отличие от всех остальных термодинамических характеристик, довольно просто померить экспериментально, определив концентрацию изучаемого вещества в воде и неполярной среде (которые, как мы помним, почти не смешиваются) и разделив одно на другое. За коэффициент гидрофобности принимают логарифм этого коэффициента — logP.
На предсказание этого коэффициента направлено несколько эмпирических методов, сводящихся к тому, чтобы на основе «обучающего набора» веществ с точно измеренным logP определить вклады отдельных фрагментов молекулы или даже отдельных ее атомов (учитывая химическое окружение), чтобы потом рассчитать гидрофобность для неизвестных молекул на основе вычисленных фрагментарных или атомных констант гидрофобности [19]. Фактически, это попытка сопоставить каждому атому в молекуле «гидрофобный заряд», хотя нужно иметь в виду, что это лишено физического смысла. Суммирование этих констант для всех атомов в молекуле даст искомое значение logP, а применение подхода, аналогичного расчету электростатического потенциала в точках пространства (φ ~ q/r), дало начало зарекомендовавшему себя в молекулярном моделировании методу Молекулярного Гидрофобного Потенциала (МГП [20]; рис. 7). Расчетам МГП посвящена программа PLATINUM [21].
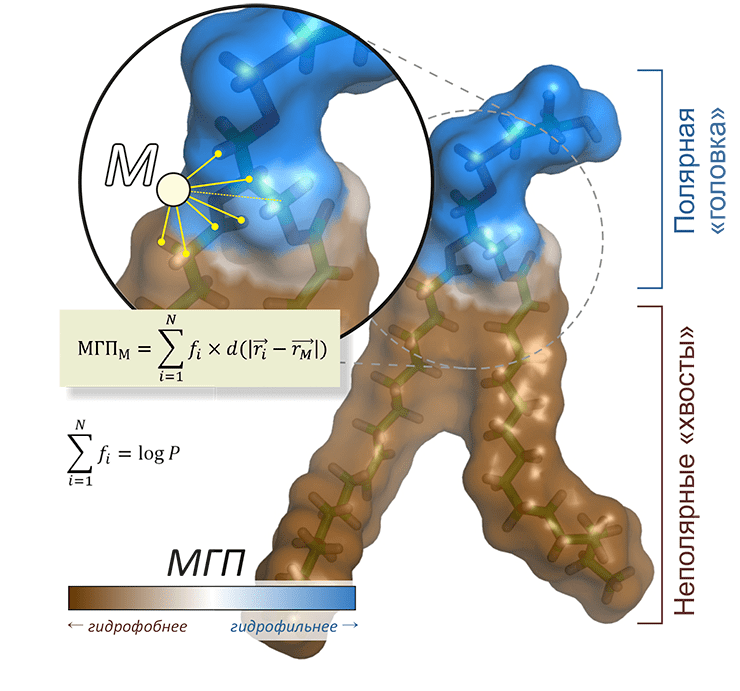
Рисунок 7. Молекулярный Гидрофобный Потенциал (МГП). Смысл подхода МГП, позволяющего рассчитывать пространственное распределение гидрофобных/гидрофильных свойств, заключается в установлении эмпирической системы атомных констант гидрофобности (fi), технически аналогичных парциальным зарядам. Сумма этих констант по всем атомам даст оценку коэффициента гидрофобности logP (где P — коэффициент распределения вещества между водой и октанолом), а вычисление «потенциала» от системы точечных «гидрофобных зарядов» с учетом затухания в пространстве (по закону d(r), равному, например, 1/r) позволяет представить себе распределение гидрофобности на молекулярной поверхности. На рисунке изображены гидрофобные свойства основного фосфолипида плазматической мембраны эукариот — пальмитоилолеилфосфатидилхолина.
Расчет МГП позволяет оценить эффективное значение гидрофобности того или иного фрагмента молекулы и наглядно визуализировать гидрофобные свойства ее поверхности, а это, в свою очередь, может рассказать о механизмах межмолекулярного взаимодействия и указать путь к направленному изменению свойств молекул или способа их взаимодействия между собой. Так, с помощью пространственного картирования гидрофобных свойств коротких α-спиральных антимикробных пептидов (АМП [22]) удалось выявить, что этим молекулам присуща амфифильная природа — когда одна сторона спирали гидрофобная, а другая — полярная и положительно заряженная. Этот мотив хорошо заметен на картах-«развертках» МГП, подчеркивая механизм взаимодействия пептида с мембраной и антимикробного действия (рис. 8). С помощью таких карт удалось модифицировать природный АМП латарцин, создав аналоги, которые обладают высокой антибактериальной активностью, но не разрушают эритроциты, а, значит, являющиеся потенциальным прототипом лекарственного препарата (рис. 8).
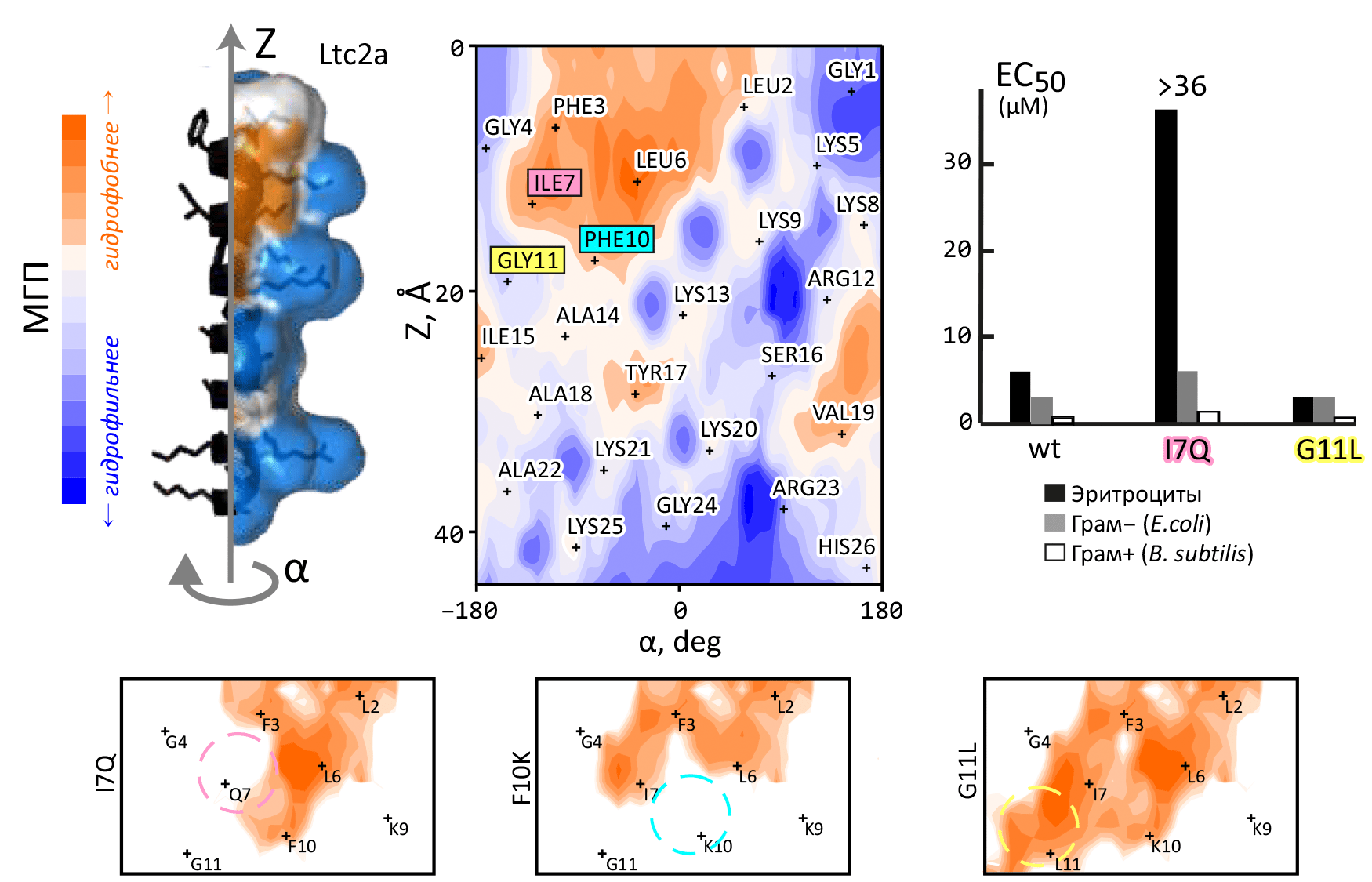
Рисунок 8. Дизайн полезных свойств в антимикробном пептиде латарцине 2a (Ltc2a). В верхнем ряду слева показано пространственное строение Ltc2a и распределение гидрофобных свойств (см. рис. 7) на его поверхности. В центре приведена карта-«развертка» МГП в цилиндрических координатах (α; Z). На ней заметен четкий амфифильный паттерн, определяющий взаимодействие пептида с мембраной клеток. В верхнем ряду справа показана цитолитическая активность пептида: он достаточно эффективно убивает как бактерии («грам+», «грам−»), так и клетки животных («эритроциты») [столбец «wt»].
Задача стояла следующая: сохранив антимикробную активность, устранить гемолитическую активность (т.е., создать прототип бактерицидного лекарства). Было сделано предположение, что изменение характера гидрофобного «пятна» на карте МГП изменит взаимодействие с мембранами бактерий и эритроцитов по-разному, и задачу удастся выполнить. Проверили три пептида, в которые ввели точечные мутации: Ile7→Gln, Phe10→Lys и Gly11→Leu. Соответствующие изменения гидрофобного паттерна показаны на трех фрагментах карт внизу. Один мутант — Ile7→Gln — обладал нужными активностями: высокой бактерицидной и низкой гемолитической.
Учет гидрофобных свойств биомолекул находит применение и в других областях молекулярного моделирования — в частности, при предсказании положения в аминокислотной последовательности трансмембранных участков или уточнении пространственной структуры комплексов рецептор—лиганд на основе принципа гидрофобного соответствия.
Несмотря на сложную физическую природу феномена гидрофобности, даже весьма поверхностный его учет в молекулярном моделировании может принести пользу. Из приведенного примера видно, что пространственное картирование свойств молекул, рассчитанное с помощью методики МГП, позволяет провести связь между структурой молекулы пептида и его активностью, а это является давней мечтой химиков, биологов и фармакологов. Умение находить такую связь обозначает возможность рационально конструировать требуемые свойства в молекулах, что, безусловно, востребовано и в фундаментальных исследованиях, и в биотехнологиях, и в медицине [24].
И снова слово о воде
Пристальный взгляд на гидрофобный эффект позволяет понять, что речь идет фактически о статистическом поведении большого числа молекул, которое описывается законами термодинамики и статистической физики. Но интереснее здесь другое — мы в очередной раз убеждаемся в уникальности такого простого, казалось бы, вещества, как вода. Вода и сама по себе имеет множество удивительных качеств [25], но в роли биологического растворителя она не имеет себе равных. Взаимодействуя с другими молекулами, вода меняет свою динамику и структуру, заставляя измениться всю систему целиком. Именно это мы наблюдаем, когда изучаем самоорганизацию амфифильных молекул в бислои и везикулы — ведь именно вода «заставляет» их собираться в такие сложные формы.
Роль воды сложно переоценить и в жизни главных биологических «машин» — белков. Их сворачивание из линейной цепочки в плотную глобулу, в которой каждый атом знает свое место — тоже заслуга воды. А значит, вода заслуживает также титул одной из самых биологических молекул, хотя по химической классификации это неорганическое вещество.
Недаром многие шарлатаны и фантазеры наделяют воду чуть ли не магическими свойствами [26], да и «обычных» ученых ее «великая тайна» волнует не меньше. Но где вода — там и гидрофобный эффект, все еще скрывающий много неизученного и просто не понятого.
Статья написана при поддержке РФФИ (конкурс на написание научно-популярных статей), № проекта: 12-04-1150212-c. В сокращенном виде она опубликована в «Природе» [27].
Литература
- Абрамзон А.А. (1982). Возьмем за образец лист лотоса. «Химия и жизнь». 11, 38–40;
- David Quéré. (2002). Fakir droplets. Nature Mater. 1, 14-15;
- Липидный фундамент жизни;
- Блинов Л.М. (1989). Молекулы-русалки. «Наука и Жизнь». 4;
- Кукушкин Ю.Н. Мыла и моющие средства // Химия вокруг нас. М.: «Высшая школа», 1992;
- Эткинс П. Порядок и беспорядок в природе. М.: «Мир», 1987. — 224 с.;
- Nelson D.L. and Cox M.M. Lehninger Principles of Biochemistry, 4th Edition. W. H. Freeman, 2004;
- W. Kauzmann. (1959). Some Factors in the Interpretation of Protein Denaturation. Advances in Protein Chemistry. 1-63;
- David Chandler. (2005). Interfaces and the driving force of hydrophobic assembly. Nature. 437, 640-647;
- Молекулярная динамика биомолекул. Часть I. История полувековой давности;
- I. T. S. Li, G. C. Walker. (2011). Signature of hydrophobic hydration in a single polymer. Proceedings of the National Academy of Sciences. 108, 16527-16532;
- Philip Ball. (2011). More than a bystander. Nature. 478, 467-468;
- P. W. Snyder, J. Mecinovic, D. T. Moustakas, S. W. Thomas, M. Harder, et. al.. (2011). Mechanism of the hydrophobic effect in the biomolecular recognition of arylsulfonamides by carbonic anhydrase. Proceedings of the National Academy of Sciences. 108, 17889-17894;
- Moran Grossman, Benjamin Born, Matthias Heyden, Dmitry Tworowski, Gregg B Fields, et. al.. (2011). Correlated structural kinetics and retarded solvent dynamics at the metalloprotease active site. Nat Struct Mol Biol. 18, 1102-1108;
- Торжество компьютерных методов: предсказание строения белков;
- Недоупорядоченные белки;
- За пределами порядка;
- Tara Hessa, Hyun Kim, Karl Bihlmaier, Carolina Lundin, Jorrit Boekel, et. al.. (2005). Recognition of transmembrane helices by the endoplasmic reticulum translocon. Nature. 433, 377-381;
- Arup K. Ghose, Vellarkad N. Viswanadhan, John J. Wendoloski. (1998). Prediction of Hydrophobic (Lipophilic) Properties of Small Organic Molecules Using Fragmental Methods: An Analysis of ALOGP and CLOGP Methods. J. Phys. Chem. A. 102, 3762-3772;
- Roman Efremov, Anton Chugunov, Timothy Pyrkov, John Priestle, Alexander Arseniev, Edgar Jacoby. (2007). Molecular Lipophilicity in Protein Modeling and Drug Design. CMC. 14, 393-415;
- Timothy V. Pyrkov, Anton O. Chugunov, Nikolay A. Krylov, Dmitry E. Nolde, Roman G. Efremov. (2009). PLATINUM: a web tool for analysis of hydrophobic/hydrophilic organization of biomolecular complexes. Bioinformatics. 25, 1201-1202;
- Антимикробные пептиды — возможная альтернатива традиционным антибиотикам;
- Anton A. Polyansky, Alexander A. Vassilevski, Pavel E. Volynsky, Olga V. Vorontsova, Olga V. Samsonova, et. al.. (2009). N-terminal amphipathic helix as a trigger of hemolytic activity in antimicrobial peptides: A case study in latarcins. FEBS Letters. 583, 2425-2428;
- Драг-дизайн: как в современном мире создаются новые лекарства;
- Петрянов И.В. Самое необыкновенное вещество в мире. М.: «Раритет», 1998;
- Здесь покоится тот, чьё имя начертано было на воде;
- Чугунов А.О., Полянский А.А., Ефремов Р.Г. (2013). Физическая водобоязнь. «Природа». 1, 24–34.