Молекулярная динамика биомолекул. Часть II. Пионерские работы отечественных ученых
20 февраля 2026
Молекулярная динамика биомолекул. Часть II. Пионерские работы отечественных ученых
- 393
- 0
- 1
Тетрапептид Триптофан—Лейцин—Фенилаланин—Аланин, который советские ученые изучали методом молекулярной динамики в 1980-х гг. В 1985 г. про него был снят целый фильм, и в этой статье мы представим его вам!
Рисунок в полном размере.
иллюстрация Анастасии Самоукиной
-
Авторы
-
Редакторы
-
Рецензенты
-
Иллюстратор
Метод молекулярной динамики (МД) прочно вошел в арсенал физиков, химиков и, конечно, биологов, поскольку дает возможность узнать подробности движения сложных молекулярных систем. В нашей стране он стал использоваться с 1970-х годов. Наверняка вы хоть раз видели красочные анимации с «ожившими» белками или ДНК, которые колеблются и двигаются в пространстве. Трудно представить, каким образом в советских НИИ на громоздких ЭВМ создавалось то, что сейчас делается на суперкомпьютерах.
В этой статье, возрождающей Спецпроект по молекулярной динамике, мы расскажем о пионерах метода МД в СССР, которые воссоздали то, что происходит в природе, в оперативной памяти компьютера. Вы узнаете, как советские ученые провели первое в мире моделирование полимера и через какие этапы они прошли, чтобы заложить основы современной структурной биоинформатики.
Молекулярная динамика

Молекулярная динамика — не новичок среди биоинформатических дисциплин, и в последние годы ее сильно подвинули подходы на базе искусственного интеллекта. Однако пока ИИ проходит «пик завышенных ожиданий», физически подкрепленные МД-методики достигают «плато продуктивности», позволяя строить корректные модели биомолекул и рассчитывать важные характеристики, используемые, например, в фармацевтической разработке. В этом спецпроекте мы продолжим давно начатый рассказ, уделив внимание и истории, и современному состоянию методики, и ее будущим перспективам.
Партнер спецпроекта — компания BIOCAD, одна из крупнейших российских биотехнологических компаний. BIOCAD заслужил серьезные позиции на мировом фармацевтическом рынке благодаря выпуску лекарственных препаратов на основе антител.
В основополагающей статье цикла «Молекулярная динамика биомолекул. Часть I. История полувековой давности» [1], вышедшей — страшно представить! — почти 20 лет назад, была описана история возникновения метода МД, изложены основные принципы и представлены первые вехи в его развитии и применении. Однако развитие МД-исследований в нашей стране и вклад отечественных ученых обсуждены не были. Именно эту часть истории мы хотим восполнить здесь — тем более, что советскими и российскими учеными был сделан ряд по-настоящему пионерских работ.
В процессе подготовки статьи неоценимую помощь нам оказали Николай Кириллович Балабаев, ведущий научный сотрудник Института математических проблем биологии Российской Академии наук в Пущино; и Константин Вольдемарович Шайтан, профессор кафедры биоинженерии биологического факультета МГУ имени М.В. Ломоносова — одни из пионеров в области применения численных расчетов для моделирования динамики молекул. Они согласились рассказать нам, как все начиналось, в серии интервью, которые были записаны в 2025 году и являются приложением к этой статье .
При подготовке данного материала мы также ориентировались на ряд публикаций Э. Э. Шноля и других авторов в книге «Метод молекулярной динамики в физической химии» [2] (в частности, статью «А. Г. Гривцов и молекулярная динамика — начало»); воспоминания Э. Э. Шноля и его коллег [3]; статьи И. М. Неелова [4], П. Г. Халатура [5], К. В. Шайтана, Р. Г. Ефремова [6], Г. Г Маленкова [7]; книгу «Методы компьютерного моделирования для исследования полимеров и биополимеров» [8]; серию статей к юбилею журнала «Высокомолекулярные соединения» [9]; и книгу к 100-летию М. В. Волькенштейна [10], содержащие историческую информацию о развитии метода МД. Авторы выражают благодарность Павлу Геннадьевичу Халатуру за консультации по истории молекулярного моделирования. Исторические статьи и интервью собраны на странице MD_history Группы интегративной биологии МГУ.
Предпосылки развития молекулярного моделирования в СССР
Какой в те годы была вычислительная техника?
Исторически возникновение и развитие молекулярного моделирования (рис. 1) в первую очередь определялось повышением производительности электронно-вычислительных машин (ЭВМ) и их доступностью для проведения научных исследований.
Первой цифровой полностью электронной ЭВМ, программируемой под решение любых задач (в терминах информатики — обладающей полнотой по Тьюрингу) была американская ENIAC (рис. 2А), запущенная в декабре 1945 года в Университете Пенсильвании. Основанная на вакуумных электронных лампах (их там было около 17 000), она могла совершать до 5000 арифметических операций в секунду (примерно в 1000 раз быстрее существовавших на тот момент лучших электромеханических компьютеров) и изначально предназначалась для расчета параметров запуска артиллерийских снарядов.
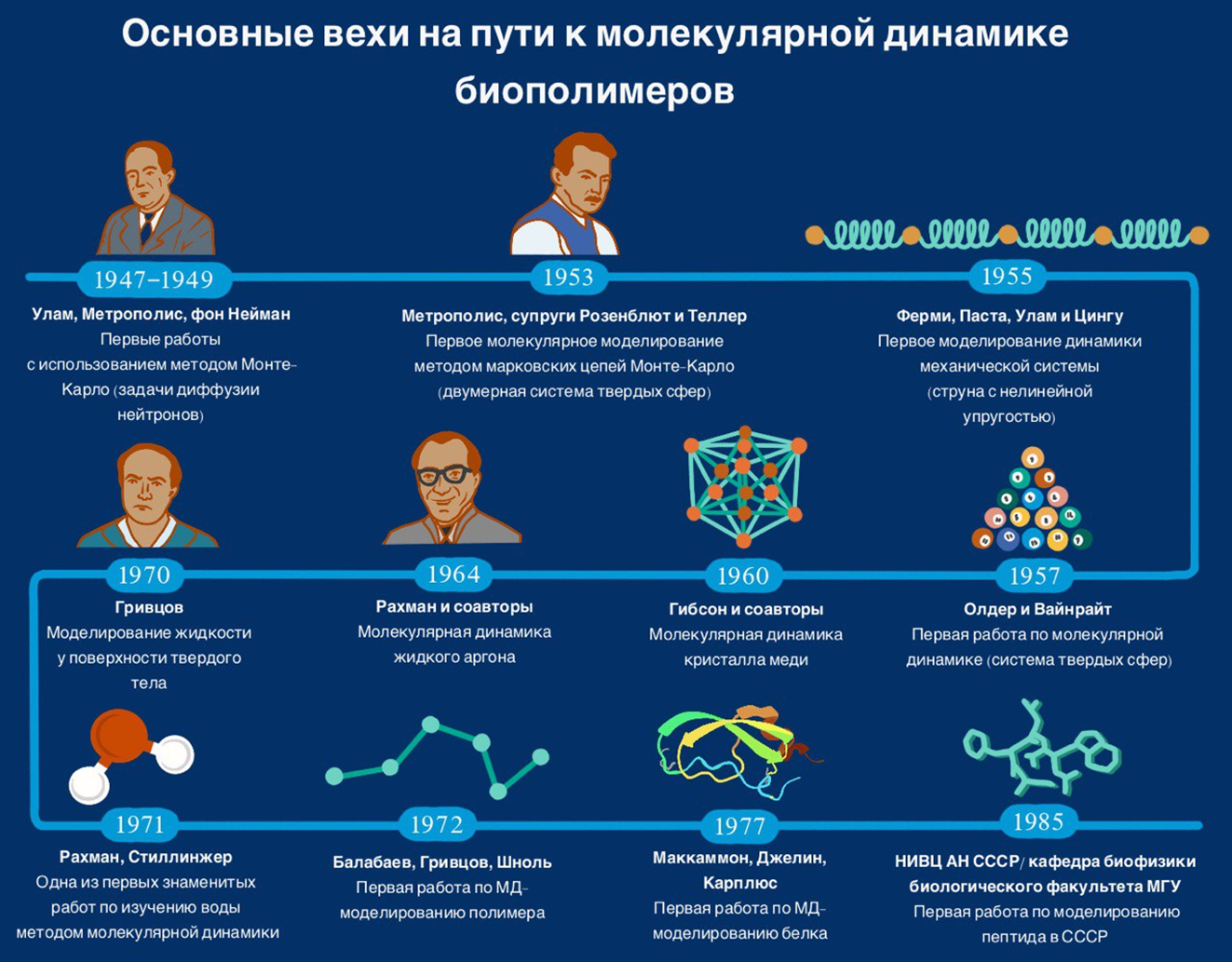
Рисунок 1. Таймлайн «Основные вехи на пути к молекулярной динамике биополимеров». Некоторые важные результаты были уже описаны в первой части спецпроекта [1]: работы Метрополиса, супругов Розенблют и Теллер; Олдера и Вайнрайта [11]; Рахмана [12]; Маккамона, Джелина и Карплюса [13]. Здесь мы дополняем этот список достижениями советских ученых: Гривцова, Балабаева и Шноля, которые первыми в мире провели численное моделирование полимера (раздел «Первое в мире численное моделирование — в СССР»); и коллективов кафедры биофизики биологического факультета МГУ и НИВЦ АН СССР (раздел «На пути к моделированию биологических макромолекул — первые расчеты пептидов и белков»). Мы также посчитали нужным добавить работы Ферми, Паста, Улама и Цингу; Гибсона [14]; Рахмана и Стиллинжера [15].
иллюстрация Анастасии Самоукиной
В 1948 году Джон и Клара фон Нейман (рис. 3) вместе с Николасом Метрополисом провели на ENIАC первые расчеты по моделированию диффузии нейтронов в ядерной реакции методом Монте-Карло [16]. В 1953 году Метрополисом в соавторстве с супругами Розенблют и Теллер было опубликовано уже первое моделирование квази-молекулярной системы — группы твердых шаров — методом марковских цепей Монте-Карло на компьютере MANIAC I, способном выполнять до 10 000 операций в секунду.
Следует отметить, что драйвером в развитии первых ЭВМ в середине 20 века в США являлись главным образом запросы военно-промышленного комплекса — так, MANIAC I создавался Н. Метрополисом в Национальной Лаборатории Лос Аламоса для решения задач, связанных с созданием водородной бомбы. Однако вскоре на рынке появились достаточно производительные ЭВМ для гражданского применения, а в развитии компьютерной техники важную роль начал играть спрос со стороны реального сектора экономики. Так, первые расчеты системы твердых сфер методом молекулярной динамики были опубликованы Олдером и Вайнрайтом в 1957 году и выполнены уже на компьютере IBM-704 (рис. 2Б в крутилке) гражданского назначения, совершавшем до 40 000 операций в секунду.

Рисунок 3. Супруги фон Нейман. Джон фон Нейман (1903–1957) — венгеро-американский математик, работавший в самых разных областях. Он развивал аппарат теории игр, изучал «язык» квантовой механики — линейные операторы — и, что наиболее важно для нашего рассказа, работал в области информатики. Джона фон Неймана по праву можно считать отцом современных компьютеров — в своей архитектуре фон Неймана он первый описал идею устройства, хранящего данные и исполняющего программы. Клара Дан-фон Нейман (1911–1963) — венгеро-американский математик, одна из первых программистов. Ее работы по численным методам и кодированию лежали в основе вычислительных прорывов Джона фон Неймана.
Перспективы применения ЭВМ не могли не быть очевидными и ряду советских ученых и организаторов науки (тем более, что с 1946 года информация об ENIAC уже была в печати). Первопроходцами в создании ЭВМ в СССР стали коллектив академика Сергея Лебедева (рис. 4) в Институте электротехники в Киеве и коллектив члена-корреспондента АН СССР Исаака Брука в Энергетическом институте в Москве. В 1950 году в Киеве запускается первая советская ЭВМ МЭСМ (малая электронно-счетная машина; рис. 2В), а в 1951 году в Москве — ЭВМ М-1. Машины обладали скромной производительностью в несколько десятков операций в секунду, существовали в единственном экземпляре и функционировали в режиме секретности, однако достаточно быстро были задействованы для важных расчетов.

Рисунок 4. Лебедев Сергей Алексеевич (1902–1974) — один из пионеров советского компьютерного машиностроения. Под его руководством было разработано 15 типов ЭВМ. Именно он построил первую ЭВМ в СССР — Малую электронно-счетную машину (МЭСМ), а затем Большую электронно-счетную машину (БЭСМ).
ЭВМ, способные рассчитывать тысячи операций в секунду, появились уже к 1953 г. — например, М-2 Исаака Брука. Его соратник Башир Рамеев вместе с Юрием Базилевским запустил в том же году производство первой серийной в СССР ЭВМ Стрела, проводившей около 2000 операций в секунду (правда, серия составила всего 7 машин). Сергей Лебедев, переехав в 1950 году в Москву и позднее возглавив Институт точной механики и вычислительной техники (ИТМиВТ) на Ленинском проспекте, сконцентрировался на разработке суперЭВМ серии БЭСМ (большая электронно-счетная машина). БЭСМ-1, построенная в 1953 году, выполняла до 10 000 операций в секунду и аппаратно поддерживала операции с плавающей запятой, что делало ее удобной для научных расчетов и ставило в ряд лучших ЭВМ мира того времени. Ряд следующих версий БЭСМ — БЭСМ-2, БЭСМ-4 и родственная им M-20 — могли проводить до 20 000 операций в секунду и были поставлены в серийное производство.
Однако настоящий прорыв в вычислительных возможностях случился с созданием БЭСМ-6 в 1967 году (см. рис. 2Г и врезку ниже). БЭСМ-6 была уже выполнена не на вакуумных лампах, а на полупроводниковых транзисторах (так называемые ЭВМ второго поколения), могла выполнять до 1 миллиона операций в секунду и имела ряд важных архитектурных усовершенствований. С 1968 по 1987 год было выпущено 355 таких суперЭВМ, и они стали поистине рабочими лошадками для советской вычислительной математики. Для БЭСМ-6 было разработано специфическое программное обеспечение, включая операционные системы и компиляторы, которые обеспечивали поддержку широкого спектра научных и инженерных задач. БЭСМ-6 активно использовалась в Советском Союзе в научных, военных и космических исследованиях. Она использовалась для расчетов в аэродинамике, ядерной физике и других высокотехнологичных областях.
Первые БЭСМ-6 в конце 1960-х гг. были поставлены в ключевые центры развития и применения вычислительной математики. Одним из таких знаковых центров был созданный в 1953 году в Москве Институт прикладной математики АН СССР (ИПМ). Его организатором и директором был (1953–1978 гг.) академик М. В. Келдыш (будущий президент АН СССР; рис. 5). ИПМ занимался решением сложных математических проблем, связанных с государственными программами исследования космического пространства, программами развития атомной и термоядерной энергетики. Для этого широко использовалась вычислительная техника, создавалось программное обеспечение. Так, в ИПМ разрабатывалось системное программное обеспечение для суперЭВМ, включая БЭСМ-6. Именно на базе ИПМ начнется история молекулярного моделирования, о чем мы расскажем в следующем разделе.

Рисунок 5. Мстислав Всеволодович Келдыш (1911–1978) — советский ученый в области прикладной математики и механики, президент Академии наук СССР (1961–1975). После окончания физико-математического факультета МГУ в 1931 году, работал в Центральном аэродинамическом институте (ЦАГИ) и параллельно учился в аспирантуре Математического института имени В.А. Стеклова. Ученый достиг больших успехов в аэро- и гидродинамике. Например, им была разработана математическая теория флаттера (опасные колебания в крыльях самолета, приводящие к авариям). Разработка Келдыша помогла предотвратить крушения советских самолетов во времена Великой Отечественной войны. Кроме того, М.В. Келдыш участвовал в строительстве космических ракет, в ядерном проекте, в создании ЭВМ и вычислительных алгоритмов для них.
В 1970–1980-х годах развитие компьютерной техники в мире все более ускорялось. В 1976 году в США Сеймур Крей разработал суперкомпьютер Cray-1, который мог выполнять 160 миллионов операций в секунду. В СССР за линейкой БЭСМ последовало семейство оригинальных суперкомпьютеров Эльбрус, разработанных все тем же ИТМиВТ; однако они уже значительно уступали по производительности лучшим мировым аналогам, и по большей части использовались для решения задач, связанных с военно-промышленным комплексом (в том числе в работе систем противоракетной обороны).
В то же время становилось понятным, что практически важным является не только быстродействие компьютеров, но и их массовая доступность, наличие программного обеспечения, удобство программирования, отладки, ввода-вывода информации, совместимость программ и периферийных устройств. В конце 1960-х годов в СССР был принят курс на создание семейства компьютеров для массовых нужд народного хозяйства, копировавших архитектуру линейки компьютеров класса мейнфреймов фирмы IBM System/360/370 и совместимое с ней программное обеспечение (в том числе, операционную систему OS/360). Для развития мировой компьютерной техники System/360 сыграла определяющую роль, задав многие стандарты в отрасли (например, что в одном байте содержится 8 бит). В СССР данная линейка машин получила название ЕС ЭВМ (Единая система электронных вычислительных машин). Всего с 1971 по 1998 годы было выпущено более 15 000 компьютеров системы ЕС, некоторые старшие модели этой линейки превосходили по производительности БЭСМ-6 и также использовались для научных расчетов, пока им на смену не пришли более знакомые нам сегодня архитектуры и операционные системы (x86, ОС Windows, Unix, Linux), но это уже тема для другой статьи.
Вклад советских ученых в развитие описания межмолекулярных взаимодействий

Рисунок 9. Владимир Александрович Фок (1898–1974) — ленинградский физик-теоретик. В 1916 году поступил в Петроградский университет, затем добровольцем пошел на фронт. Работал в разных институтах, включая Государственный оптический институт и Ленинградское государственное училище (теперь СПбГУ). Ученый оставил неизгладимый след в науке, существенно продвинул квантовую механику и квантовую теорию поля.
Как уже обсуждалось в статье «МД биомолекул. Часть I. История полувековой давности» [1], для реализации подходов молекулярного моделирования требуются не только вычислительные мощности, но и сформулированные на языке математики модели молекул и их взаимодействий (а также численные алгоритмы, позволяющие исследовать эти модели с помощью ЭВМ). Если представить молекулу как механизм, то силовое поле (англ. force field) — это инструкция, описывающая все «пружинки» и «магниты», которые удерживают атомы вместе и управляют их движением. Точнее: силовое поле описывает силовые константы и способ расчета функции энергии взаимодействия между атомами, которая состоит из нескольких слагаемых — термов, — описывающих валентные (связи, углы) и невалентные (ван-дер-ваальсовы, электростатические) взаимодействия.
Методы описания силовых полей появились в 1960-х, и уже тогда для определения некоторых констант силового поля — зарядов системы — использовали методы квантовой химии, позволяющие взглянуть на электронную структуру атомов и с помощью нее рассчитать необходимые значения. Улучшение точности моделирования молекул было бы невозможно без теоретической базы квантово-механических расчетов, заложенной еще в начале 30-х годов. Работы советского физика-теоретика Владимира Александровича Фока (рис. 9) значительно уточнили метод приближенного решения уравнения Шрёдингера, который предложил английский физик Дуглас Хартри в 1927 году.

Рисунок 10. Александр Исаакович Китайгородский (1914–1985) — выдающийся советский физик-кристаллограф. В 1935 году окончил физический факультет МГУ, после работал во многих институтах, включая Всесоюзный институт экспериментальной медицины и Институт элементоорганических соединений. Автор нескольких учебников по рентгеноструктурному анализу и популяризатор науки: если читателям интересна научно-популярная литература по физике, то Александром Китайгородским вместе с Львом Ландау была написана целая серия книг «Физика для всех».
С тех пор этот ключевой для квантовой химии подход носит фамилии двух ученых: метод Хартри–Фока есть почти во всех пакетах для квантово-химических расчетов. Из расчетов можно получить информацию об электронной структуре молекул и о ее свойствах.
Разработка силовых полей связана с понятием молекулярной механики (ММ), которого мы уже касались в первой части цикла статей об МД [1]. Считается, что пионерами в применении метода для расчета взаимодействия атомов в молекулах являются Вестхаймер и Хилл, но одновременно и независимо к идее моделирования конформаций пришел и наш соотечественник — кристаллограф Александр Исаакович Китайгородский (рис. 10). Хотя название «молекулярная механика» Китайгородский не использовал, теоретические основы ММ были заложены именно им.
Сформулированный ученым принцип плотной упаковки, гласящий, что молекулы в кристалле стремятся заполнить все пустоты, натолкнул Китайгородского на идею представления невалентных взаимодействий. Так, Китайгородский первым предложил рассматривать внутри- и межмолекулярные взаимодействия с помощью одинаковых математических выражений и параметров. Он выводил их эмпирически, изучая молекулярные кристаллы углеводородов. Это были удобные системы, поскольку в них доминировал вклад невалентных взаимодействий, причем Кулоновским можно было пренебречь из-за малых атомных зарядов. Переходя от простых систем к более сложным, ученый постепенно вывел выражения потенциалов, которые зависели от расстояний между атомами (отчего к потенциалу еще применяют термин «атом-атомный потенциал» [19]). Результаты, полученные Александром Исааковичем Китайгородским, стали базой и вдохновением для большого числа работ [1], [19], [20].
Научная литература и распространение научной информации
Для разговора о развитии методов молекулярной динамики в СССР уместно обсудить, насколько хорошо первые работы, опубликованные на западе, были известны советским ученым; и в целом — как распространялась информация о научных достижениях в СССР и между странами. В эпоху повсеместного использования интернета и ИИ для быстрого поиска и доступа к информации многие уже не имеют представления о том, как осуществлять поиск научных статей вручную в библиотечных фондах. В «доинтернетовскую» эпоху данная задача решалась с помощью специальных библиотечных каталогов, предметных указателей и реферативных журналов.
В целом, задачам доступа и каталогизации научно-технической информации (в том числе и издаваемой за рубежом) в СССР уделялось достаточно много внимания. В 1952 году был создан Всесоюзный институт научно-технической информации (ВИНИТИ) АН СССР, в задачи которого входила каталогизация и обработка всей научно-технической информации, публикуемой в мире. Интересно, что институт научной информации (ISI), ныне известный как Web of Science, был создан в США лишь четыре года спустя, фактически как ответ на создание ВИНИТИ [21]. Таким образом, у советских ученых была возможность доступа ко многим западным научным изданиям — правда, с рядом оговорок. Во-первых, доступ к подшивкам журналов был далеко не во всех библиотеках, и зачастую ученым приходилось ехать в центральные библиотеки Москвы (например, Ленинскую библиотеку) для того, чтобы ознакомиться с той или иной статьей. Во-вторых, поиск нужных статей по тематике был достаточно трудоемким процессом, требовавшим активных действий, поэтому многие потенциально интересные статьи могли не попадать в поле зрения ученого сразу.
Если говорить о пионерской работе Олдера и Вайнрайта по МД 1957 года [11], то она уже была подробно разобрана в книге «Статистическая теория жидкостей» известного белорусского физика-теоретика Иосифа Залмановича Фишера 1960 года [22] . Вероятно, Фишер — первый популяризатор метода МД в СССР. В 1959 году он опубликовал обзорную статью в журнале «Успехи физических наук» [23], в которую включил результаты, полученные Олдером и Вайнрайтом. Вообще статья была посвящена обзору метода Монте-Карло, но, как отметил И. З. Фишер, он намеренно решил «включить этот материал [статью по МД Олдера и Вайнрайта] в обзор из-за его исключительного интереса для статистической физики, а также из-за тесной связи полученных при этом результатов с результатами метода Монте-Карло».
Олдер и Вайнрайт впервые представили науке результаты моделирования методом МД еще в 1956 году на Брюссельском симпозиуме по транспортным процессам в статистической механике в докладе Molecular dynamics by electronic computers.
Еще одна особенность научных публикаций в «доцифровую» эпоху — относительная краткость, отсутствие цифровых и дополнительных материалов. Так, оригинальная статья (точнее, письмо в журнал Journal of Chemical Physics) Олдера и Вайнрайта была объемом всего в 1 журнальную страницу — сродни статье Уотсона и Крика 1953 года об открытии двойной спирали ДНК [24]. Правда, в 1959–1969 годах ими уже были написаны две более подробные статьи, раскрывающие суть метода [25], [26].
В Советском Союзе в 1970-х издавалось около 800 научных журналов. Ряд журналов по естественным наукам переводился на английский язык и был доступен западным читателям. На начало 1960-х журналов, которые переводились официально, было уже более 120. Однако журналы переводились далеко не всегда в полном объеме. Так, например, пионерская работа по МД полимера Н.К. Балабаева, А.Г. Гривцова и Э.Э. Шноля, опубликованная в 1975 году в Докладах Академии Наук СССР [27], по-видимому, не была переведена на английский язык.
Отметим еще один интересный способ обнародования научных результатов — это препринты. Сейчас, с развитием онлайн серверов типа arxiv.org, bioRxiv.org и подобных, практика размещения рукописей научных статей в открытом доступе до их отсылки на рецензирование в научный журнал стала широко применяться. Препринты открывают быстрый доступ к результатам исследований всем желающим, причем бесплатно, в то время как публикация в журнале может занимать от месяцев до нескольких лет. Препринты особенно актуальны для быстроразвивающихся направлений научных исследований — например, во время эпидемии COVID-19 они были основным оперативным источником информации о научных исследованиях по биологии вируса и методах терапии.
Однако оказывается, что культура препринтов существовала и до появления интернета, так как это был способ быстро разослать/зафиксировать результат до журнальной публикации. В физике (и смежных областях) инфраструктура препринтов оформлялась уже в конце 1950-х и в 1960-х гг. в крупных международных центрах (например, в CERN), где «неформальный обмен рукописями» постепенно превратился в системный поток с каталогизацией и правилами. В биологии первые попытки систематизировать правила публикации и обмена препринтами предпринимались в Национальных институтах здоровья также в начале 1960-х [28].
В СССР культура институтских препринтов также существовала: в ряде научных центров их статус приравнивали к научной публикации (например, в Объединенном институте ядерных исследований в Дубне [29], в ИПМ им. Келдыша [30]); публикации распространялись по библиотекам, каталогизировались, могли продаваться в специализированных магазинах. Таким образом, препринт мог быть одновременно и «быстрой научной рассылкой», и вполне «издательским объектом» с ценой в копейках, тиражом и распространением по библиотекам. Ряд первых работ по МД в СССР как раз был представлен в виде препринтов серии ИПМ им. Келдыша, которая выходит с 1967 года до сих пор.
Первое в мире численное моделирование полимера — в СССР

Рисунок 11. Аллан Георгиевич Гривцов (1937–1991) — советский и российский физик. Выпускник кафедры биофизики физического факультета МГУ. Работал в Институте фотосинтеза и Институте Прикладной Математики, затем перешел в Институт Физической Химии РАН (ИФХ РАН), где проработал 20 лет. Один из основоположников применения метода МД в СССР.
Зарождение идеи о численном моделировании движения молекул в СССР имеет общие черты с тем, как это складывалось за океаном. Во-первых, идея и первая реализация произошла в институтах, основной задачей которых были закрытые разработки (так, ИПМ АН СССР до 1966 года функционировал в секретном режиме). Во-вторых, первые научные вопросы, на которые хотели ответить исследователи, были связаны с поведением неупорядоченных сред — жидкостей, теоретическое исследование которых аналитическими методами сложнее, чем кристаллических материалов или газов.
Итак, в Советском Союзе идея об использовании ЭВМ для численного моделирования движения молекул впервые была сформулирована и реализована Алланом Георгиевичем Гривцовым (1937–1991; рис. 11) и Эммануилом Эльевичем Шнолем (1928–2014; рис. 12). По воспоминаниям соратника А. Г. Гривцова Г. Г. Маленкова, размышлять о возможности использования ЭВМ для решения задачи движения молекул, и что таким образом можно исследовать жидкости, Аллан Георгиевич начал, еще будучи студентом физического факультета МГУ, кафедру биофизики которого он закончил в 1965 году. Уже став сотрудником Института фотосинтеза в г. Пущино весной 1966, А. Г. Гривцов выступил с серией докладов в ИПМ на неофициальном семинаре, посвященном математическим вопросам естествознания, где рассказал о современных на тот момент теориях жидкости.
Пущино — наукоград, построенный с нуля в конце 1950-х – начале 1960-х годов в Московской области для создания Научного центра биологических исследований АН СССР, и объединивший 9 институтов академии наук в области биофизики, молекулярной биологии и смежных наук.
Теории жидкостей несовершенны и не всегда согласуются друг с другом. А нельзя ли „посмотреть“ на структуру жидкости, рассчитав взаимодействие и движение ее молекул с помощью вычислительной машины? Мысль моя, как видно, была наивной; никаких работ в этом направлении я не знал и был лишь наслышан (из популярных статей) о сложной структуре воды.

Рисунок 12. Эммануил Эльевич Шноль (1928–2014) — советский и российский математик. Поступил на мехмат МГУ, когда ему было 15 лет, в 1943 году. После службы в армии поступил в аспирантуру в Математический институт им. М. И. Стеклова и защитил диссертацию, связанную с изучением свойств решений уравнения Шрёдингера. Ученый работал над задачей во время службы в армии — по воспоминаниям Эммануила Эльевича, это был его лучший математический труд. Итогом стала теорема Шноля, которая послужила толчком для многих работ в области изучения свойств оператора Штурма—Лиувилля. В 1958 году был принят на работу в Институт Прикладной Математики, в котором проработал более 20 лет. Под его началом в России начал развиваться метод молекулярной динамики [31].
Эта дискуссия в дальнейшем переросла в сотрудничество. Уже через год совместной работы в отчете «О численном моделировании движения молекул жидкости» (1967) Гривцов и Шноль изложили революционную для того времени идею моделирования движения небольшого числа молекул в приповерхностных слоях жидкости. Первые расчеты выполнялись на ЭВМ Стрела. Осмыслению задачи помогли находки в зарубежных журналах — в том числе «та самая» статья 1957 года Олдера и Вайнрайта [11].
Результаты работ Аллана Гривцова по моделированию методом МД были представлены в нескольких сборниках трудов в 1969 и 1970 годах. Главная сила работ происходила из слабостей метода: в те времена возможно было рассчитывать траектории движения атомов только для небольших систем. Поэтому Гривцов изначально сфокусировался на процессе, в котором участвует порядка сотни молекул — взаимодействии молекул одноатомной жидкости с плоской поверхностью. Ученый смог узнать детали, скрытые от глаз экспериментаторов: он проанализировал численные результаты и уже по ним «увидел», как ведет себя одноатомная жидкость вблизи поверхности. Например, было выяснено, что молекулы жидкости упорядочиваются у отражающей границы, выстраиваются в кристаллоподобные структуры. При этом температура «кристаллизации» у поверхности превышала температуру кристаллизации в объеме [7].

Рисунок 13. Препринт ИПМ о численных экспериментах Балабаева, Гривцова и Шноля. По словам Николая Кирилловича Балабаева (рис. 14), «препринт ИПМ — это фактически научная статья, выпущенная в институте. Основная часть результатов, скажем, у математиков на тех же защитах диссертаций была описана в них. Статус препринтов был очень высок, потому что они проходили внутреннюю рецензию сотрудников ИПМ. И если работу пропускали, то это значило, что работа признавалась. Конечно, это не мешало публиковать статьи, как и в случае любого препринта — хоть дублируй в статью — это не есть нарушение, это не есть плагиат».
В 1970 г. Аллан Гривцов издал первую журнальную статью в СССР, в которой использовался метод молекулярной динамики: «О структурировании жидкостей у поверхности твердого тела» [32]. Возможности МД позволяли проводить численные эксперименты при различных значениях параметров систем: температуры, отношением числа частиц к объему (иначе говоря, плотности). Проведенный Гривцовым анализ показал, что жидкость в системе приобретает слоистую структуру — этот вывод согласовывался и с предыдущими работами. Варьируя параметры, ученый смог смоделировать случай, не рассмотренный ранее, когда вблизи плоской поверхности находились молекулы пара, а в глубине — молекулы жидкости. При помощи численного эксперимента ученому удалось воспроизвести переходный слой между жидкостью и паром.
За авторством Гривцова и Шноля в 1971 году были изданы два препринта Института прикладной математики: о структурировании жидкости у отражающей границы и об ее адсорбции. Эти работы входили в цикл «Численные эксперименты по моделированию движения молекул» (рис. 13) и составляли первую и вторую части [33], [34]. В этих препринтах метод МД (который А. А. Гривцов предпочитал называть численными экспериментами динамического типа — ЧЭДТ) позиционировался Гривцовым и Шнолем именно как метод «численных экспериментов».
А. Г. Гривцов всегда уделял большое внимание строгости и корректности применения методов компьютерного моделирования или „имитации“, как любил он говорить. Дело в том, что в англоязычной литературе эта деятельность обычно называется „computer simulation“. Русский эквивалент „симуляция“ вызывает негативные ассоциации, поэтому А. Г. Гривцов предпочитал говорить об имитации или численных экспериментах. Обычно употребляемый термин „моделирование“ слишком широк и недостаточно конкретен.

Рисунок 14. Николай Кириллович Балабаев (род. 1948) — советский и российский биофизик. Окончил Московский Физико-Технический Институт в 1972. Дипломная работа была посвящена моделированию полимерной цепочки (рис. 15) — первому в мире. С 1972 работает в Институте математических проблем биологии РАН в г. Пущино, кандидат наук (1990) и заведующий лабораторией молекулярного моделирования.
Чуть ранее, в 1969 году, к группе присоединился Николай Кириллович Балабаев (рис. 14), тогда еще студент МФТИ, который выбрал Эммануила Шноля в качестве научного руководителя для написания диплома. Выпускная работа, а вместе с ней и третья, заключительная, часть цикла «Численные эксперименты по моделированию движения молекул» (1972), содержали совершенно новые результаты (рис. 15) [5].
Балабаев, Шноль и Гривцов провели первое в мире моделирование динамики полимера. Полимер состоял из атомов, соединенных абсолютно жесткими связями — то есть, расстояние между соединенными атомами было постоянно. Такую систему можно представить себе как шарики-атомы, скрепленные жесткими стержнями-связями. Для изучения молекул в приближении жестких связей был разработан оригинальный алгоритм численного решения уравнений движения.
При помощи метода МД ученым удалось изучить несколько моделей полимеров разной длины. Все полимеры рассматривались изолированно, то есть в отсутствии молекул растворителя, в вакууме. Описанный в препринте полимер состоял из 26 атомов (было рассчитано ~300 пс динамики системы, включающей ~60 000 счетных шагов). Работы по моделированию первого полимера проводились уже на БЭСМ-6, а программа писалась на автокоде БЕМШ — аналоге языка ассемблер.
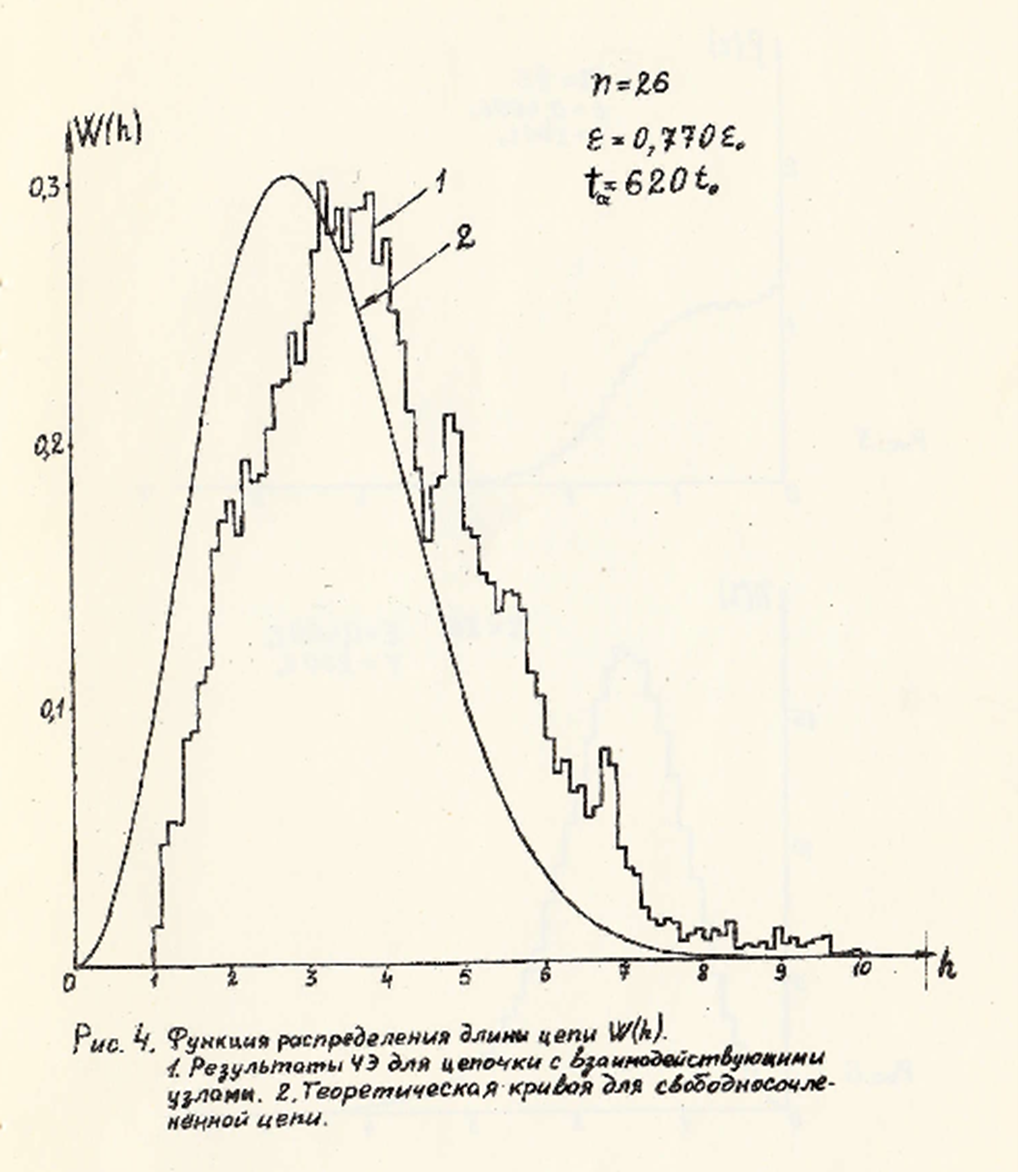
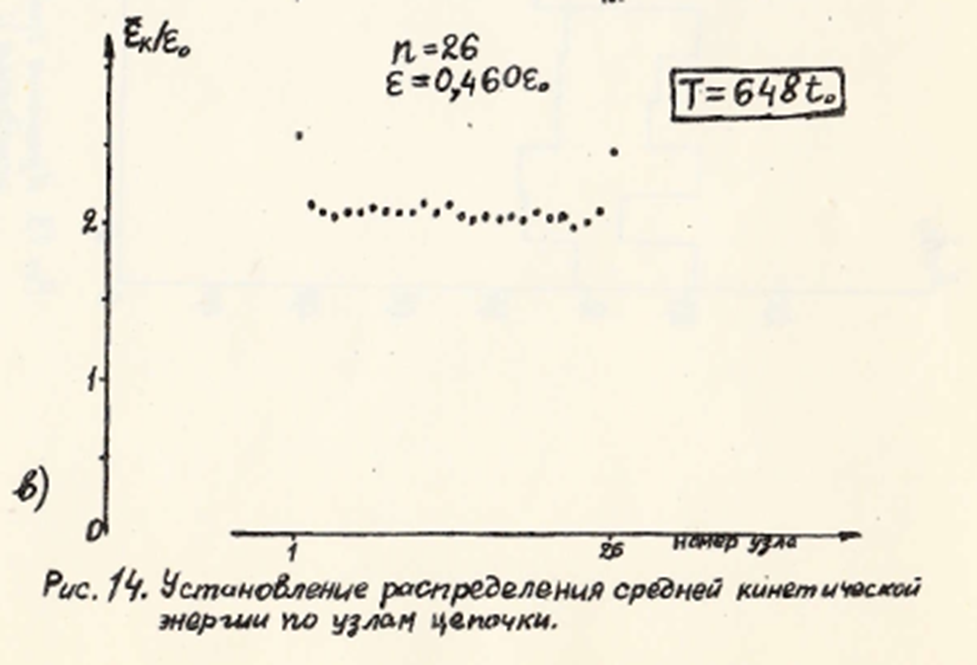
Главный результат — открытие эффекта «горячих концов» — актуален до сих пор. Ученые обнаружили, что концы полимера движутся в среднем на 15–20% быстрее, чем атомы в середине. Эффект «горячих концов» наблюдался и для более длинных полимеров, состоящих из 101 атома. Полученные результаты позволили лучше понять особенности динамического поведения реальных молекул, для которых справедливо приближение жестких связей, — например, для полиэтилена. Тем самым, в СССР было положено начало компьютерному моделированию полимеров — обширного класса соединений, к которому относятся нуклеиновые кислоты, углеводы, белки. В 1975 году результаты препринта о моделировании полимера были выпущены в виде статьи в журнале Доклады Академии наук [35].
Развитие методов молекулярной динамики полимеров в СССР
С 1967 А. Г. Гривцов перешел на работу в Институт Физической Химии в Москве (ныне — Институт физической химии и электрохимии им. Фрумкина), где возглавил кабинет математических методов исследований и продолжил пропаганду возможностей метода МД среди физхимиков. Для Э. Э. Шноля и Н. К. Балабаева в начале 1970-х также начинается новый период. В 1972 году в Научном центре биологических исследований РАН в Пущино усилиями А. М. Молчанова и Э. Э. Шноля, при поддержке М. В. Келдыша, С. Э. Шноля и Г. М. Франка, организуется новый институт — Научно-исследовательский вычислительный центр, НИВЦ (позднее переименованный в Институт математических проблем биологии, ИМПБ РАН). Задача нового центра — вычислительные исследования в области биологии и поддержка таких исследований в других институтах. Одним из первых сотрудников НИВЦ становится Н. К. Балабаев.
Возможности, открывшиеся по применению метода МД для изучения линейных молекул в результате работ Балабаева и коллег, были замечены специалистами по теоретическому исследованию полимеров. Нужно отметить, что к концу 1960-х в СССР сложилась школа теоретической физики полимеров и позднее биополимеров главным образом под руководством чл.-корр. РАН Михаила Владимировича Волькенштейна и его учеников в Институте Высокомолекулярных Соединений (ИВС) в Ленинграде, а позднее в Институте Молекулярной Биологии в Москве и Институте биофизики в Пущино (см., например, классические книги М. В. Волькенштейна «Конфигурационная статистика полимерных цепей», 1959, и «Молекулы и жизнь. Введение в молекулярную биофизику», 1965).
Чуть позднее важным центром исследований теории полимеров стала школа под руководством академика Ильи Михайловича Лифшица на физическом факультете МГУ, которую он развивал вместе со своими учениками А. Р. Хохловым (ныне академиком РАН, заведующим кафедрой физики полимеров и кристаллов физического факультета МГУ) и А. Ю. Гросбергом.
Отметим также, что моделирование полимеров в простейших решеточных моделях методом Монте-Карло уже было освоено сотрудниками ИВС (Крон, Ельяшевич, Птицын и др.) в середине 1960-х [36]. К середине 1970-х с помощью такого моделирования удавалось получать интересные результаты и о «заузливании» молекул ДНК (см. статью в журнале Nature Statistical mechanics and topology of polymer chains 1975 года за авторством Франк-Каменецкого, Лукашина и Вологодского [37]). В начале 1970-х моделирование воды методом Монте-Карло уже проводилось Саркисовым и Дашевским [38] в Институте биофизики в Пущино; позднее к этим работам присоединился Г. Г. Маленков [39], [40], приглашенный А. Г. Гривцовым на работу в Институт физической химии.
Знакомство ученых ИВС с работами Балабаева, Гривцова и Шноля произошло в результате визита А. М. Ельяшевича (ученик М. В. Волькенштейна, он возглавил лабораторию М. В. Волькенштейна после переезда последнего в Москву) в Ленинскую библиотеку в Москве . В библиотеке А. М. Ельяшевич нашел соответствующие препринты, понял, что это была абсолютно новая, революционная работа, и привез копии препринтов в свой институт. Сотрудники ИВС высоко оценили данные работы и решили связаться с авторами — и вышли на Н. К. Балабаева. Завязалось тесное сотрудничество, которое послужило стимулом развития методов МД полимеров как в Ленинграде, так и в Пущино и Москве. Ключевую роль в этом сыграло сотрудничество пущинской группы с Анатолием Анатольевичем Даринским, Юлием Яковлевичем Готлибом и Игорем Михайловичем Нееловым. Начиная с 1976 года, обе группы работали вместе над развитием метода и его применений для исследования полимерных и биополимерных систем.
В те времена именно библиотеки выступали в роли «открытых баз данных» научной информации — поэтому поездки ученых в библиотеки даже в другой город для изучения новых научных трудов были не редкостью. Подробнее мы написали об этом в главе «Научная литература и распространение научной информации».
В 1978 году была опубликована статья в журнале «Высокомолекулярные соединения» под авторством Балабаева, Готлиба, Даринского и Неелова, в которой моделировали полимер из 123 атомов, соединенных жесткими связями [41]. Особенности такой модели знакомы нам уже из второго раздела статьи. В отличие от работы Балабаева (1972), ученые исследовали систему, состоящую из множества одинаковых ячеек. Такую конструкцию еще называют системой в периодических граничных условиях: одной и той же ячейкой с молекулой периодически «мостят» все пространство. В полученную сетку из полимеров — полимерную матрицу — также включали дополнительные частицы, чтобы наблюдать их диффузию сквозь нее. Сами численные эксперименты проводились при трех температурах. В начале генерировалась случайная конформация цепи, а затем запускался расчет (было рассчитано ~61 пс динамики системы, включающей ~13 000 счетных шагов). Каждый отдельный случай занимал два часа расчетного времени БЭСМ-6, то есть за сутки можно было посчитать 732 пс. Для сравнения, современный суперкомпьютер Anton 3 имеет скорость расчета до 100 мкс в день для гораздо более сложных молекулярных систем [42]!
В дальнейшем Готлиб, Даринский и Неелов продолжили свои исследования в области физики полимеров и молекулярной динамики. Их работы сыграли ключевую роль в понимании механизмов движения полимеров — ими были написаны различные учебные пособия и дан импульс развитию ленинградской школы МД полимеров.
В Москве группой Гривцова совместно с Институтом химической физики (там работал бывший аспирант А. Г. Гривцова М. А. Мазо) и НИВЦ в Пущино в 1970–80-х годах также был сделан ряд интересных работ по моделированию молекулярных кристаллов и полимеров, в частности, изучению деформаций кристаллов, процессов стеклования [7].
Вероятно, не менее значимой для развития молекулярного моделирования полимеров (и в дальнейшем биополимеров) была организационная деятельность А. Г. Гривцова в конце 1970-х — начале 1980-х по проведению Всесоюзных семинаров (совещаний) по применению математических методов для исследования полимеров. Последний семинар 1985 года носил название «IV Всесоюзное совещание „Математические методы для исследования полимеров и биополимеров“», что отражало усиление интереса в направлении моделирования биологический полимеров.
Первый такой семинар состоялся в ИФХ в 1978 году, остальные в Пущино в 1979, 1981, 1983 и 1985 годах. А. Г. Гривцов старался привлечь к работе в семинарах ученых, работающих в разных областях естествознания, причем не только немногих в то время специалистов по компьютерному моделированию, но и чистых математиков, физиков-теоретиков и даже экспериментаторов. Он стремился находить новые сферы приложения методов компьютерного моделирования, заинтересовать этими методами как можно больше исследователей. Чтобы участники семинаров были лучше подготовлены к обсуждению докладов, легче воспринимали материал и более активно участвовали в дискуссиях, А. Г. Гривцов просил основных докладчиков подготовить препринты, своевременное опубликование которых было возможно только благодаря его активности и энергии. Препринты содержали, конечно, гораздо больше подробностей, чем можно было донести до слушателей в устном докладе. Эти препринты могли служить полезным руководством по тем или иным проблемам математического моделирования полимеров и биополимеров. В процессе общения участников семинаров друг с другом родилось немало новых идей, создавались неформальных коллективы, начинались оригинальные исследования.
По воспоминаниям Э. Э. Шноля, «в одном из перерывов совещания 1979 г. А. Г. высказал такую мысль: полезно бы устроить в Москве постоянно действующий семинар „Математические методы для исследования полимеров“. Участвовавшие в совещании Александр Юльевич Гросберг и Алексей Ремович Хохлов взялись помочь в организации семинара и, в частности, поговорить со своим научным руководителем Ильей Михайловичем Лифшицем. Илья Михайлович согласился возглавить этот семинар, и семинар вскоре начал работать». Заседания этого «Семинара по теории полимеров» с тех пор регулярно происходят на физическом факультете МГУ.
На пути к моделированию биологических макромолекул — первые расчеты пептидов и белков
После периода гонений на генетику, связанных с деятельностью Т. Д. Лысенко, развитие молекулярной биологии и биофизики активизировалось в СССР с середины 1950-х. Этому способствовало известное письмо трехсот ведущих биологов и физиков в президиум ЦК КПСС в защиту генетики в 1955 году, основание кафедр биофизики биологического (1953) и физического (1959) факультетов МГУ, принятие решения о строительстве Пущинского биологического научного центра (1956), открытие новых лабораторий соответствующего профиля в ведущих институтах АН СССР.
Значительный вклад в развитие теоретического описания биополимеров внес М. В. Волькенштейн, принявший решение сместить фокус своих исследований в сторону биополимеров. Отметим также, что с середины 1970-х гг. в сферу актуальных научных проблем стали входить вопросы динамики белков. Связано это в значительной мере с появившимися новыми экспериментальными возможностями (прежде всего, различные спектроскопические методы). Стало понятно, что подвижность белков необходима для выполнения ими своих функций. Успехи структурной биологии в расшифровке структур белков, хотя и способствовали прояснению функций, но далеко не всегда объясняли их полностью. Классический пример — молекула миоглобина. В ней гем — центр связывания кислорода — находится внутри белковой глобулы, и каким образом туда проникает кислород, из статичной структуры было непонятно.
Одним из наиболее чувствительных методов исследования внутренней динамики на середину 1970-х годов был метод мессбауэровской спектроскопии, основанный на эффекте Мессбауэра, открытом Рудольфом Мессбауэром в 1950-х годах. Научная общественность была сильно взволнована тем, что изменения формы мессбауэровской линии при изменении температуры в случае белков была непохожа на соответствующие эффекты ни в твердых телах, ни в жидкостях или стеклах. После визита Р. Мессбауэра в Москву в 1979 году и обсуждения данной проблемы, теоретическое объяснение эффекта Мессбауэра в белках, а с ним и важные выводы о характере динамики белков были даны сотрудником кафедры биофизики биологического факультета МГУ Константином Вольдемаровичем Шайтаном [43]. Основа наблюдаемых эффектов оказалась в отличии динамики белков (а также многих других макромолекул с конформационной подвижностью) от обычных твердых тел или жидкостей. Это отличие состоит в том, что амплитуды движения атомов в несколько раз больше, чем в твердых телах, но все же ограничены в пространстве, а само движение происходит диффузионным образом. Основной вклад в эффекты дает резкое уменьшение вязкости микроокружения атомных групп при увеличении температуры (впоследствии это стали называть ограниченной диффузией).
Интерес к динамике биологических молекул, знакомство с первыми работами группы Карплюса по динамике белков (1977 [13], 1979 [44] годы) естественным образом ставили вопрос о начале работ по молекулярному моделированию биологических молекул методом МД и в нашей стране. Однако переход к реальным объектам со сложной структурой требовал серьезного совершенствования программного кода — автоматической генерации списков взаимодействующих атомов и параметров их взаимодействий на основе некоторых правил, называемых силовым полем. За такую задачу с конца 1970-х годов взялся Н. К. Балабаев со своими сотрудниками, разрабатывая оригинальную программу PUMA/ПУМА (от слов Пущинский макромолекулярный анализ).
Следует отметить, что, хотя метод Монте-Карло технически более сложен в адаптации к моделированию биологических молекул, которые имеют сложную разветвленную структуру и чья динамика в основном определяется поворотами вокруг химических связей, пионерские работы по моделированию ДНК в СССР были выполнены именно этим методом. В частности, отметим работы Ульянова и Журкина 1982 года из Института молекулярной биологии — первое моделирование ДНК (1982) [45]; Данилова и др. — моделирование урацила в воде (1984) [46]; Теплухина и др. — моделирование ДНК в воде (1989) [47].
Подступаться к моделированию сложных биологических макромолекул начали постепенно. Этому способствовало знакомство Н. К. Балабаева с рядом ученых на Всесоюзных семинарах в Пущино, о которых мы писали выше. Важную роль сыграло знакомство с ученым из Калининского (ныне Тверского) государственного университета Павлом Геннадьевичем Халатуром. С конца 1970-х гг. П. Г. Халатур занимался моделированием полимеров методом Монте-Карло, уделяя особое внимание полимерам, конформационная динамика в которых реализовывалась за счет вращения вдоль химических связей (такие модели уже описывали реальные полимеры — например, полиэтилен) [3], [32]. Он составил несколько учебных пособий по вычислительным методам — например, «Машинный эксперимент в конформационном анализе полимеров» (1982).
Кроме этого, П. Г. Халатур был одним из первопроходцев в изучении программ МД, которые писались на Западе. В частности, с 1978 года уже существовала программа GROMOS, разрабатываемая в университете Гронингена в Голландии. Обмен опытом с П.Г. Халатуром помогал и в разработке программы ПУМА. У ученых завязалось сотрудничество по моделированию молекул липидов — основных компонентов биологических мембран. В 1986 ученые опубликовали статью по моделированию липидного бислоя методом МД в журнале Molecular Physics [48]. В качестве липидов брали модели, состоявшие из 16 «бусин», соединенные абсолютно жесткими связями. При помощи них ученые изучали свойства липидного слоя как такового. Работа послужила важным заделом для построения моделей реальных биологических мембран. В 1986 году у П. Г. Халатура и соавторов вышла статья по моделированию целлюлозы [49].
Свой черед ждали и первые работы по моделированию белков. Важную роль для осмысления МД-подходов к динамике белков сыграла обзорная статья Гривцова и соавторов по МД белков, изданная в 1983 году [50]: фактически с ее публикацией началось активное обсуждение и планирование работ по моделированию полипептидов в СССР.
В 1983 году на Всесоюзном совещании Н. К. Балабаев познакомился с К. В. Шайтаном, который к тому моменту изучал динамику белков с использованием эффекта Мессбауэра (см. выше). Было решено инициировать сотрудничество и начать с наиболее простых белковых объектов — пептидов. Первой совместной работой стало моделирование тетрапептида Триптофан—Лейцин—Фенилаланин—Аланин в вакууме и в гидрофобном растворителе. Всего в системе с растворителем насчитывалось 300 атомов: 257 атомов растворителя и 43 атома системы (использовалось тяжелоатомное приближение, когда атомы водорода как бы эффективно «включались» в атомы кислорода, углерода и азота). Было рассчитано от 6,5 до 14,0 пс динамики каждой системы. Результаты данной работы были включены в диссертационную работу А. Ю. Кузьминова «Молекулярная динамика тетрапептидов и их равновесные структуры» [51], защищенную под руководством К. В. Шайтана 12 марта 1987 года. Результаты также были опубликованы в трудах второй всесоюзной конференции «Математические вычислительные методы в биологии. Биомолекулярные системы» [52].
В результате данной работы был достигнут и значимый результат в молекулярной визуализации — получена анимация траектории МД белкового объекта (видео 1; рис. 17). Этот фильм был снят во Владивостоке в НИИ автоматики и процессов управления ДВНЦ АН СССР благодаря деятельности О. С. Кислюка и сотрудников, которые занимались разработкой программ молекулярной графики. Фильм снимался покадрово с экрана ЭВМ; его съемка потребовала визита московских ученых.
Видео 1. Фильм о динамике тетрапептида — 1985 год. Вот как появление этого фильма было прокомментировано самим автором диссертации: «С этой целью при участии автора и сотрудников Научно-исследовательского Вычислительного центра АН СССР в г. Пущино: Н. К. Балабаева, Л. В. Луневской, А. А. Нурисламова, А. Г. Мурзина, Р. М. Борисюка; и сотрудников кафедры биофизики биологического факультета Московского Государственного университета: К. В. Шайтана, И. В. Упорова, а также сотрудников Научно-исследовательского института автоматики и процессов управления ДВНЦ АН СССР О. С. Кислюка, Т. А. Боровиной был снят десятиминутный научный цветной фильм „Молекулярная динамика тетрапептидных молекул“». Источник цитаты: выдержка из диссертации А. Ю. Кузьминова [51].
VK Видео. Оцифровка видео проведена в.н.с. кафедры биоинженерии биологического факультета МГУ Г. А. Армеевым

Рисунок 17. На такую бобину был записан фильм о МД пептида.
К концу 1980-х — началу 1990-х гг. относятся первые работы по моделированию методом МД целых белков. Первой работой в СССР в этом направлении, по-видимому, является работа Халатура и Павлова 1990 года по моделированию инсулина в сборнике научных трудов Равновесная динамика структуры биополимеров [53]. Для расчета использовался МД-пакет SIMOL, разработанный в КГУ П. Г. Халатуром и Ю. Г. Папуловым [54]. В программе ПУМА первое моделирование белка ферредоксина (100 пс при температуре 300K) стартовало в начале 1990-х гг. и было опубликовано в 1996 году за авторством Н. К. Балабаева, А. С. Лемака и К. В. Шайтана [55].
В 1990-е годы и далее активное развитие и применение методов МД велось в Московском университете в Группе молекулярной динамики под руководством профессора К.В. Шайтана (сегодня сайт группы заархивирован). Целая серия работ конца 1990-х и начала 2000-х была посвящена систематическому изучению динамики небольших пептидов. Была изучена динамика всех 400 дипептидов, 8000 трипептидов, 16000 некоторых тетрапептидов как в условиях виртуального растворителя, так и в водной среде. Кластерный анализ авто- и кросскорреляционных функций поворотов по торсионным углам показал (этого раньше не предполагалось), что имеется очень высокая степень динамического подобия для определенных групп этих углов. Позднее стало понятно, что большой вклад в такого рода эффекты дают корреляции вращений по торсионным углам, вызванные вязкостью среды и минимизацией энергетических потерь на вязкое трение [56], что, по-видимому, способствует быстрому фолдингу белка и выходу из парадокса Левинталя. Работами этой же группы была существенно расширена область применения МД и к другим молекулярным объектам. В частности, стала моделироваться динамика различных наноструктур (нанотрубки, фуллерены и др.), процессы взаимодействия наноструктур с биомембранами и полимерами, процессы функционирования ионных каналов, динамика самосборки пространственной структуры макромолекул и др.
Говоря о других научных центрах, отметим, что в 1990-е годы Балабаев начал сотрудничество с двумя учеными из Карельского научного центра Российской академии наук: Александром Львовичем Рабиновичем и Паули Онниевичем Рипатти. Вместе они приступили к задаче моделирования биологической мембраны с фосфолипидами. Предыдущие наработки сильно помогли, и в результате, начиная с 90-х, начали выходить совместные статьи.
Развитие интернета, доступность персональных ЭВМ и рост их производительности с конца 1990-х годов стали способствовать активному развитию методов МД во многих научных институтах и университетах. В том числе этому способствовали и активизировавшиеся контакты между отечественными и западными учеными, а также возможность распространения по интернету программ, протоколов, структур биологических молекул. Обсуждение развития методов МД биомолекул за последние десятилетия лежит за пределами этой статьи.
Завершая этот раздел, расскажем об исторической встрече советских и западных специалистов по молекулярной динамике (и не только) белков — о семинаре СССР—США «Белки и стекла» (рис. 18). Это был третий семинар в серии советско-американских семинаров по динамике молекулярных систем, организованный Академией наук СССР совместно с Национальной Академией наук США. Он состоялся в Черноголовке летом 1991 года — на излете эпохи СССР. На нем была широко представлена американская и советская наука. С американской стороны присутствовал и будущий нобелевский лауреат и один из основателей метода молекулярной динамики М. Карплюс. С советской стороны присутствовала также весьма представительная делегация: В. И. Гольданский (сопредседатель семинара), М. В. Волькенштейн, А. Б. Рубин, Н. К. Балабаев, Ю. Ф. Крупянский (ученый секретарь семинара), Д. С. Чернавский, К. В. Шайтан и др. Уже в те годы было понятно, что ожидается очень быстрый прогресс в вычислительной технике, и методы молекулярной динамики для изучения функционирования биосистем с атомной точностью станут незаменимыми. Так, в общем-то и случилось.

Рисунок 18. Участники семинара СССР—США «Белки и стекла» в Черноголовке, июнь 1991 г. Слева направо: У. Итон (США), Н. К. Балабаев, О. Энджел (США), М. Карплюс (США), С. Нэджел (США), Л. В. Абатуров, В. А. Бендерский, Д. С. Чернавский, А. Ю. Гросберг, А. С. Плачинда, [нрзб], Л. А. Блюменфельд, А. В. Куликов, В. Н. Морозов, [нрзб], А. И. Демченко, Г. Петско (США), Г. И. Лихтенштейн, Ю. А. Берлин, М. В. Волькенштейн, Н. С. Ованесян, В. Д. Федотов, Г. Фрауэнфельдер (США), В. Седов, В. И. Гольданский, [нрзб], Ю. Ф. Крупянский, Л. И. Трахтенберг, А. С. Давыдов, И. В. Куринов, А. Б. Рубин, В. К. Имшенник, К. В. Шайтан, В. Я. Рочев, П. Волинес (США), И. В. Упоров, Г. Модзолевский (США), Ю. А. Лебедев, И. П. Суздалев, К. Мейо (США), [нрзб], Ф. Стиллинджер (США).
архив Юрия Федоровича Крупянского
Мы предлагаем читателям посмотреть интервью с Николаем Кирилловичем Балабаевым и Константином Вольдемаровичем Шайтаном, в которых они делятся своими воспоминаниями про становление метода МД — во многом именно они стали базой для данной статьи.
Видео 2. Интервью с Николаем Кирилловичем Балабаевым: Молекулярная динамика полимеров, ч. 1. Записано 23 апреля 2025 года на кафедре биоинженерии биологического факультета МГУ. В ходе беседы Н. К. Балабаев рассказал о ранних работах по молекулярной динамике в мире и в СССР, а также дальнейшем развитии этого направления в части молекулярной динамики полимеров и биополимеров. Также обсуждалась история вычислительной техники, прикладной математики, биофизики, включая основание и развитие Научного центра биологических исследований в Пущино.
ВК-канал Кафедры биоинженерии МГУ. Проведение интервью — А. К. Шайтан, монтаж — Г. А. Армеев.
Видео 3. Интервью с Константином Вольдемаровичем Шайтаном. Молекулярная динамика полимеров, ч. 2. Записано 5 сентября 2025 года на кафедре биоинженерии биологического факультета МГУ. В ходе беседы К. В. Шайтан рассказал о развитии представлений о динамике белков начиная с 1960-х годов, в том числе использовании методов Мессбауэровской спектроскопии, и развитии методов молекулярной динамики для исследования этих вопросов.
ВК-канал Кафедры биоинженерии МГУ. Проведение интервью — А. К. Шайтан, монтаж — Г. А. Армеев.
Заключение
Метод МД прошел большой путь с конца 1950-х годов и стал одним из важных подходов изучения структуры, динамики и функций (био)полимеров. Отрадно отметить, что первые работы по моделированию полимеров были выполнены отечественными учеными и способствовали развитию оригинальной школы молекулярной динамики в нашей стране. Запуск расчетов методом МД и получение траекторий молекулярной динамики, визуализации «молекулярного кино» сейчас доступны многим и делаются достаточно просто. Однако получение значимых, статистически и научно достоверных результатов по-прежнему требуют кропотливой работы, глубокого понимания физических и математических аспектов моделирования, осознания границ применимости моделей, использования аппарата теории случайных процессов, статистической физики и термодинамики, умения правильным образом поставить задачу, запрограммировать и запустить вычислительный эксперимент, модифицировать или дополнить программный код, интегрировать различные данные и соотнести расчеты с реальными биофизическими и биологическими экспериментами. По воспоминаниям наших собеседников, основоположник и популяризатор метода молекулярной динамики в нашей стране Аллан Гривцов отзывался об МД как о «деле для настоящих мужчин». Мы полагаем, что в наши дни он бы сформулировал ту же самую мысль несколько иначе: «Молекулярная динамика — дело для настоящих ученых!».
Литература
- Молекулярная динамика биомолекул. Часть I. История полувековой давности;
- Товбин Ю. К. Метод молекулярной динамики в физической химии. М.: «Наука», 1996. — 334 с.;
- Юдович Я. Э., Ермакова Е. А. Московский математик Эммануил Шноль. Сыктывкар: ООО «Коми республиканская типография», 2022. — 292 с.;
- Неелов И.М. Введение в молекулярное моделирование биополимеров. Санкт-Петербург: НИУ ИТМО, 2014. — 101 с.;
- P.G. Khalatur. (2012). Molecular Dynamics Simulations in Polymer Science. Polymer Science: A Comprehensive Reference. 417-460;
- Кирпичников М. П. От биоинженерии к инженерной биологии. М.: «Товарищество научных изданий КМК», 2025. — 174 с.;
- Маленков Г. Г. (2007). Компьютерное моделирование структуры и динамики атомно-молекулярных систем. Современные проблемы физической химии. 48, 119–136;
- Хохлов А. Р. Методы компьютерного моделирования для исследования полимеров и биополимеров. М.: «Либроком», 2009. — 696 с.;
- . (2009). Theory and simulation. Polym. Sci. Ser. A. 51, 49-69;
- Бирштейн Т. М., Шаронова Н. А. Михаил Владимирович Волькенштейн. Воспоминания коллег и учеников. К 100-летию со дня рождения. М., 2012. — 100 с.;
- B. J. Alder, T. E. Wainwright. (1957). Phase Transition for a Hard Sphere System. The Journal of Chemical Physics. 27, 1208-1209;
- A. Rahman. (1964). Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev.. 136, A405-A411;
- J. Andrew McCammon, Bruce R. Gelin, Martin Karplus. (1977). Dynamics of folded proteins. Nature. 267, 585-590;
- J. B. Gibson, A. N. Goland, M. Milgram, G. H. Vineyard. (1960). Dynamics of Radiation Damage. Phys. Rev.. 120, 1229-1253;
- Aneesur Rahman, Frank H. Stillinger. (1971). Molecular Dynamics Study of Liquid Water. The Journal of Chemical Physics. 55, 3336-3359;
- Thomas Haigh, Mark Priestley, Crispin Rope. (2014). Los Alamos Bets on ENIAC: Nuclear Monte Carlo Simulations, 1947-1948. IEEE Annals Hist. Comput.. 36, 42-63;
- Abhishek Singharoy, Christopher Maffeo, Karelia H. Delgado-Magnero, David J.K. Swainsbury, Melih Sener, et. al.. (2019). Atoms to Phenotypes: Molecular Design Principles of Cellular Energy Metabolism. Cell. 179, 1098-1111.e23;
- Миллисекундный барьер взят!;
- Valeri Poltev. (2017). Molecular Mechanics: Principles, History, and Current Status. Handbook of Computational Chemistry. 21-67;
- A.I. Kitaygorodsky. (1960). Calculation of conformations of organic molecules. Tetrahedron. 9, 183-193;
- Björn Hammarfelt, Johanna Dahlin. (2025). Abstracting It All: The Soviet Institute of Scientific Information (VINITI) and the Promise of Centralisation, 1952–1977. Minerva. 63, 115-133;
- Фишер И. З. Статистическая теория жидкостей. М.: Физматлит, 1960. — 280 с.;
- I.Z. Fisher. (1959). Applications of the monte carlo method in statistical physics. Успехи физических наук. 69, 349-369;
- J. D. WATSON, F. H. C. CRICK. (1953). Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature. 171, 737-738;
- B. J. Alder, T. E. Wainwright. (1959). Studies in Molecular Dynamics. I. General Method. The Journal of Chemical Physics. 31, 459-466;
- B. J. Alder, T. E. Wainwright. (1960). Studies in Molecular Dynamics. II. Behavior of a Small Number of Elastic Spheres. The Journal of Chemical Physics. 33, 1439-1451;
- Балабаев Н. К., Гривцов А. Г., Шноль Э. Э. (1975). Численное моделирование движения линейной полимерной цепочки. Докл. АН СССР. 220, 1096–1098;
- Roth P. Formalizing Informal Communication: An Archaeology of the Early Pre-Web Preprint Infrastructure at CERN. ArXiv, 22 p.;
- Ефимов Г. В., Намсрай Х. (1973). К построению нелокальной квантовой электродинамики частиц со спином 0 и 1. Лаборатория теоретической физики. — 27 с.;
- Дарьин Н. А., Мажукин В. И., Самарский А. А. (1987). Конечно-разностный метод решения стационарных двумерных краевых задач на адаптивной сетке, динамически связанной с решением. Институт прикладной математики им. М.В. Келдыша Академии наук СССР. — 32 с.;
- Шноль Э. Э. А.Г. Гривцов и молекулярная динамика — начало. // «Метод молекулярной динамики в физической химии» / Под ред. Товбина Ю.К. М., 1996. С. 10–15;
- Гривцов А. Г. (1970). О структурировании жидкостей у поверхности твердого тела. / А.Г. Гривцов // Доклады Академии наук СССР. 190, 868–871;
- Гривцов А. Г., Шноль Э. Э. (1971). Численные эксперименты по моделированию движения молекул. Ч. 1. Структурирование жидкости у отражающей границы. Институт прикладной математики, Академия наук СССР.;
- Гривцов А. Г., Шноль Э. Э. (1971). Численные эксперименты по моделированию движения молекул. Ч. 2. Адсорбция на гладкой поверхности. Институт прикладной математики, Академия наук СССР.;
- Балабаев Н. К., Гривцов А. Г., Шноль Э. Э. (1972). Численные эксперименты по моделированию движения молекул. Ч. 3. Движение изолированной полимерной цепочки. Институт прикладной математики, Академия наук СССР.;
- Крон А. К. (1965). Метод Монте-Карло для статистических расчетов макромолекул. Высокомолекулярные соединения. 7, 1228–1234;
- M. D. Frank-Kamenetskii, A. V. Lukashin, A. V. Vologodskii. (1975). Statistical mechanics and topology of polymer chains. Nature. 258, 398-402;
- Саркисов Г. Н., Дашевский В. Г. (1972). Расчет термодинамических свойств воды методом Монте-Карло. Журнал структурной химии. 13, 199;
- Саркисов Г. Н., Маленков Г. Г., Дашевский В. Г. (1973). Расчет термодинамических свойств воды методом Монте-Карло. Журнал структурной химии. 14, 6;
- G. N. Sarkisov, G. G. Malenkov, V. G. Dashevskii. (1973). A study of the structure of water by the Monte Carlo method. J Struct Chem. 14, 4-8;
- Балабаев Н. К., Готли pЮ. Я., Даринский А. А., Неелов И. М. (1978). Молекулярная динамика полимерной цепи из взаимодействующих звеньев. Времена релаксации. Высокомолекулярные соединения. 10, 2194–2201;
- David E. Shaw, Peter J. Adams, Asaph Azaria, Joseph A. Bank, Brannon Batson, et. al.. (2021). Anton 3. Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. 1-11;
- Шайтан К. В., Рубин А. Б. (1980). Конформационная подвижность и теория эффекта Мессбауэра в биологических системах (Модель броуновского осциллятора с сильным затуханием для конформационных мод). Молекулярная биология. 14, 1323–1335;
- M. KARPLUS, J. A. MCCAMMON. (1979). Protein structural fluctuations during a period of 100 ps. Nature. 277, 578-578;
- Ульянов Н. Б., Журкин В. Б. (1982). Изучение гибкости комплементарных нуклеозидфосфатов методом Монте-Карло. Молекулярная биология. 16, 1075–1084;
- V.I. Danilov, I.S. Tolokh, V.I. Poltev, G.G. Malenkov. (1984). Nature of the stacking interaction of nucleotide bases in water: a Monte Carlo study of the hydration of uracil molecule associates. FEBS Letters. 167, 245-248;
- A. V. Teplukhin, V. I. Poltev, N. V. Shulyupina, G. G. Malenkov. (1989). Monte Carlo Simulation of Hydration of the Nucleic Acid Fragments. Journal of Biomolecular Structure and Dynamics. 7, 75-99;
- P.G. Khalatur, N.K. Balabaev, A.S. Pavlov. (1986). Molecular dynamics study of a lipid bilayer and a polymer liquid. Molecular Physics. 59, 753-773;
- Khalatur P. G., Marchenko G. N., Pletneva S. G., Khrapkovskii G. M. (1986). Dokl. Akad. Nauk SSSR. 291, 157;
- Grivtsov A. G., Malenkov G. G., Abaturov, L. V. (1983). Numerical modelling of protein molecular dynamics. Mol. Biol. 17, 587–615;
- Кузьминов А.Ю. Молекулярная динамика ряда тетрапептидов и их равновесные структуры: дисс. канд. биол. наук. — Москва, МГУ им. М. В. Ломоносова, 1986;
- Балабаев Н. К., Нурисламов А. А., Упоров И. В., Шайтан К. В. Молекулярная динамика олигопептидов и их структурно-функциональная организация. // Математические и вычислительные методы в биологии. Биомолекулярные системы: Тезисы докладов, Пущино, 08–10 сентября 1987 года / Ответственный редактор В.Н. Буравцев; Академия наук СССР; Научный центр биологических исследований; Научно-исследовательский вычислительный центр. — Пущино: Научный центр биологических исследований АН СССР, 1987. – С. 3–10;
- Халатур П. Г., Павлов А. С. (1990). Молекулярно-динамическое моделирование денатурации глобулярного инсулина. Равновесная динамика структуры биополимеров. 1, 133–147;
- Халатур П. Г., Папулов Ю. Г. Методика численного моделирования на ЭВМ динамики сложных молекул. Описание библиотеки SIMOL. Калинин: КГУ, 1986. — 32 с.;
- Балабаев Н. К., Лемак А. С., Шайтан К. В. (1996). Молекулярная динамика и электронно-конформационные взаимодействия в ферредоксине. Молекулярная биология. 30, 1348–1356;
- Шайтан К. В. (2023). Почему белок сворачивается в уникальную 3D-структуру? И не только это… Химическая физика. 42, 40–62.