12 методов в картинках: «сухая» биология
01 декабря 2017
12 методов в картинках: «сухая» биология
- 14307
- 0
- 51
рисунок Ольги Пташник
-
Авторы
-
Редакторы
-
Иллюстратор
Далеко не вся наука делается в пробирках. Современная молекулярная биология немыслима без привлечения компьютеров. Огромное количество новых биологических знаний сегодня получают в «сухих» — то есть вычислительных — экспериментах. О том, что и как делают молекулярные биологи на компьютерах, вы узнаете из этой статьи.
12 биологических методов в картинках

Генеральный партнер цикла — компания «Диаэм»: крупнейший поставщик оборудования, реагентов и расходных материалов для биологических исследований и производств.
Одна из главных миссий «Биомолекулы» — докопаться до самых корней. Мы не просто рассказываем, какие новые факты обнаружили исследователи — мы говорим о том, как они их обнаружили, стараемся объяснить принципы биологических методик. Как вытащить ген из одного организма и вставить в другой? Как проследить в огромной клетке за судьбой нескольких крошечных молекул? Как возбудить одну крохотную группу нейронов в огромном мозге?
И вот мы решили рассказать о лабораторных методах более системно, собрать воедино в одной рубрике самые главные, самые современные биологические методики. Чтоб было интереснее и нагляднее, мы густо проиллюстрировали статьи и даже кое-где добавили анимации. Мы хотим, чтобы статьи новой рубрики были интересны и понятны даже случайному прохожему. И с другой стороны — чтобы они были так подробны, что даже профессионал мог бы обнаружить в них что-то новое. Мы собрали методики в 12 больших групп и собираемся сделать на их основе биометодический календарь. Ждите обновлений!
Предисловие. Что такое «сухие» методы
Биология зародилась как описательная, а не аналитическая наука. В сущности, таковой она и остается сейчас, с той лишь разницей, что значительно изменилось качество биологических знаний, точность получаемых сведений, и, безусловно, количество информации. Это стало возможным во многом благодаря развитию приборной базы и технического обеспечения науки вообще, и, в частности, компьютерных технологий, а также способов хранения и обработки информации.
«Сухие» методы в молекулярной биологии — довольно разнородная группа подходов, использующая математические методы и физические закономерности для решения разнообразных биологических проблем [1–3]. «Сухими» их назвали в противопоставление лабораторным — «мокрым» — методам, для которых характерна работа с различными биологическими и химическими растворами в пробирках. Совокупность методов и подходов к анализу и систематизации данных о биологических объектах принято называть биоинформатикой, а ученых, которые этим занимаются, соответственно — биоинформатиками [4]. Принципиально в биоинформатике можно выделить три больших направления:
- Структурная биоинформатика (методы, используемые при изучении пространственной структуры биомолекул).
- Биоинформатика последовательностей (методы анализа аминокислотных и нуклеотидных последовательностей).
- Алгоритмическая биоинформатика (математическое моделирование сложных биологических систем и процессов).
От пробирок к цифрам: история «сухой» биологии
Трудно точно определить, когда в биологической науке стали применять «сухие» методы. Известно, что уже в начале тринадцатого века математические подходы опробовали для решения биологических проблем. Так, например, знаменитый математик Леонардо Пизанский (Фибоначчи) применил принципы комбинаторики для решения задачи размножения кроликов. Однако тогда биологический контекст задачи был использован скорее в качестве украшения математической теории, чем ставил реальную и актуальную проблему, поскольку имел много серьезных допущений. Вычислительные подходы для решения реальных биологических задач впервые применили в двадцатых годах XX века. Итальянский математик Вито Вольтерра (и независимо от него американский статистик Альфред Джеймс Лотка) разработал модельные дифференциальные уравнения, описывающие совместное существование двух биологических сообществ по типу «хищник—жертва», что стало основой современной математической теории популяций, а также началом широкого распространения методов математического моделирования в биологии [5]. Тем не менее, наиболее широкое распространение вычислительные подходы получили не в популяционной, а в молекулярной биологии (рис. 1).
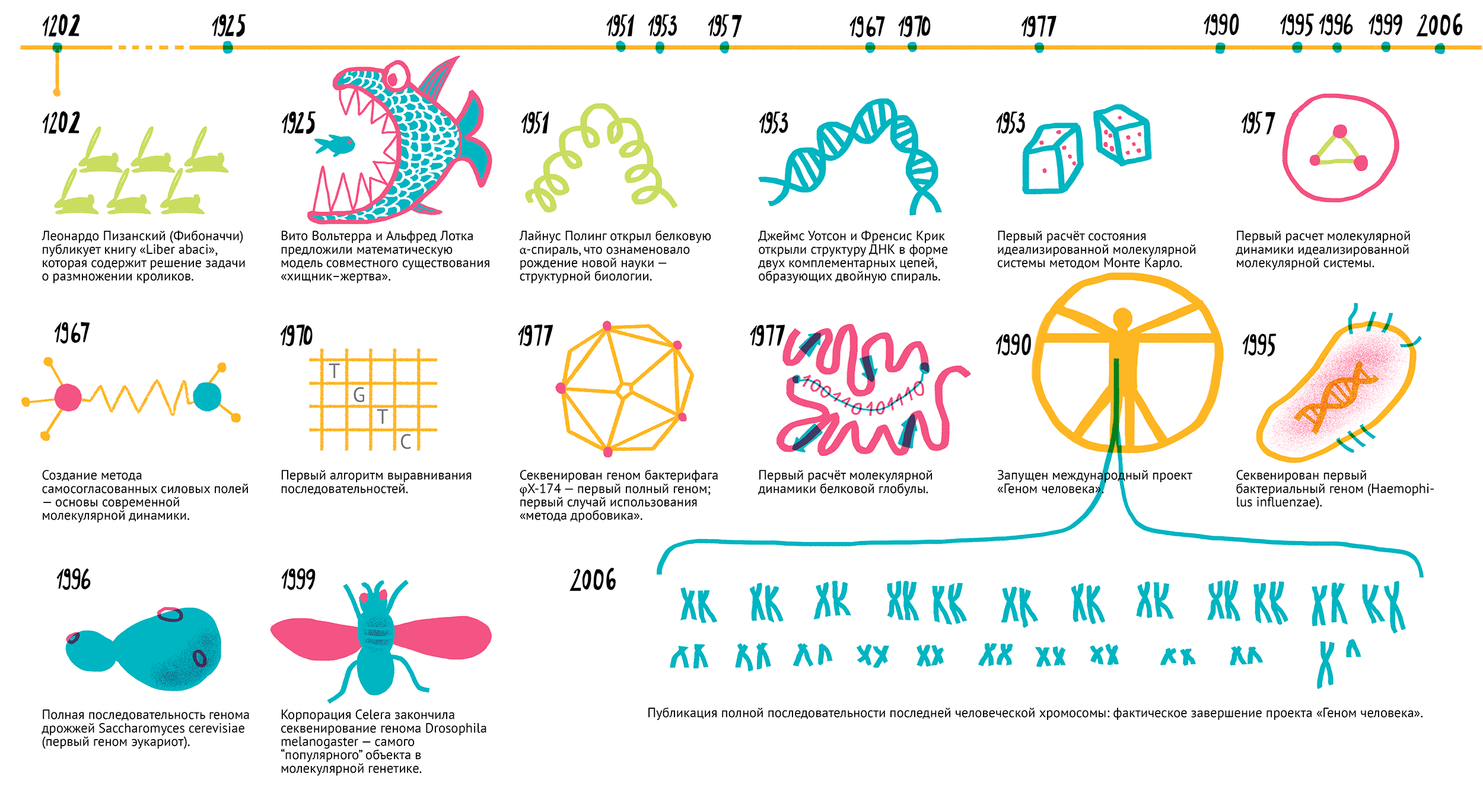
Рисунок 1. Главные вехи в развитии «сухой» биологии. 1202 г. — Леонардо Пизанский (Фибоначчи) опубликовал книгу «Liber abaci», которая содержала решение задачи о размножении кроликов. 1925 и 1926 гг. — Вито Вольтерра и Альфред Лотка предложили математическую модель совместного существования «хищник—жертва». 1950 г. — Пер Виктор Эдман предложил метод секвенирования пептидов. 1951 г. — Лайнус Полинг открыл белковую α-спираль, что ознаменовало рождение новой науки — структурной биологии [6]. 1953 г. — Джеймс Уотсон и Френсис Крик открыли структуру ДНК в форме двух комплементарных цепей, образующих двойную спираль. 1953 г. — Первый расчет состояния идеализированной молекулярной системы методом Монте-Карло. 1957 г. — Первый расчет молекулярной динамики идеализированной молекулярной системы [7]. 1964 г. — Первая система компьютерной визуализации молекул [8]. 1967 г. — Создание метода самосогласованных силовых полей — основы современной молекулярной динамики [7]. 1967 г. — Пер Эдман совместно с Джофри Бэггом создали первый автоматический белковый секвенатор. 1970 г. — Полина Хогевег предложила термин «биоинформатика». 1970 г. — Первый алгоритм выравнивания последовательностей. 1975 г. — Фредерик Сенгер предложил первый метод секвенирования ДНК [9]. 1975 г. — Первая работа по изучению белок—белковых взаимодействий с применением компьютеров. 1977 г. — Фредерик Сенгер опубликовал метод определения последовательности ДНК, «метод терминаторов», который лег в основу современного автоматического секвенирования в капиллярных секвенаторах [9]. 1977 г. — Секвенировали геном бактерифага φX-174 — первый полный геном; первый случай использования «метода дробовика». 1977 г. — Первый расчет молекулярной динамики белковой глобулы [7]. 1981 г. — Секвенировали митохондриальную ДНК человека: 16 659 нуклеотидных пар (п.н.). 1982 г. — Первая программа для молекулярного докинга. 1984 г. — Секвенировали геном вируса Эпштейна—Барр: 172 281 п.н. [10]. 1986 г. — Первый автоматический ДНК-секвенатор (Applied Biosystems, США) [9]. 1990 г. — Разработали программу BLAST. 1990 г. — Запустили международный проект «Геном человека» [11]. 1992 г. — Компания Wellcome Trust и Британский совет медицинских исследований основали The Sanger Centre (сейчас The Wellcome Trust Sanger Institute) для широкомасштабного секвенирования геномов. 1992 г. — Учредили Институт геномных исследований (The Institute for Genome Research) с целью использования секвенирования для коммерческих целей (идентификации генов и разработки лекарств). 1995 г. — Секвенировали первый бактериальный геном (Haemophilus influenzae). 1996 г. — Полная последовательность генома дрожжей Saccharomyces cerevisiae (первый геном эукариот). 1999 г. — Корпорация Celera закончила секвенирование генома Drosophila melanogaster — самого «популярного» объекта в молекулярной генетике. 1999 г. — Опубликовали полную последовательность одной из хромосом человека. 2000 г. — Окончание секвенирования генома человека (в общих чертах). 2003 г. — Реальное окончание секвенирования генома человека [11]. 2006 г. — Публикация полной последовательности последней человеческой хромосомы: фактическое завершение проекта «Геном человека».
рисунок Ольги Пташник
Развитие методов «сухой» биологии так или иначе связано с открытиями и изобретениями в «мокрой» (то есть экспериментальной) молекулярной биологии. Впрочем, это неудивительно, — биоинформатика оперирует данными о реальных биологических системах, и эти данные нужно сначала как-то получить, а уж потом анализировать и систематизировать. В связи с этим большинство ключевых событий в этой истории имеют «сугубо экспериментальные» корни.
В 1950 году шведский биохимик Пер Виктор Эдман опубликовал первую работу по определению последовательности аминокислотных остатков в пептидах с помощью химической деградации [12]; впоследствии метод назвали его именем. В 1951 году Лайнус Полинг открыл α-спираль — наиболее распространенный мотив укладки полипептидной цепи [13], — а в 1953 Джеймс Уотсон и Френсис Крик опубликовали модель структуры ДНК [14]. Этот период ознаменовал рождение новой области биологической науки, занимающейся изучением структуры биологических макромолекул — структурной биологии [6].
Физический анализ молекулярных систем
Тогда на фоне развития компьютерных технологий математику и физику стали активно применять для анализа молекулярных систем. В 1949 году Николас Метрóполис предложил стохастический математический подход, который назвал «метод Монте-Карло» [15]. Уже в 1953 году он с коллегами опубликовал первую работу по применению метода Монте-Карло для компьютерного расчета состояния идеализированной молекулярной системы [16]. Практически одновременно с Метрополисом физик Берни Адлер работал над решением подобной задачи. В результате создал первую в истории программу для расчета молекулярной динамики, названную «STEP», а в 1957 была опубликована первая работа по молекулярной динамике («динамика биллиардных шаров») [7].
В 1958 году впервые в истории установили структуру белка (миоглобина кашалота) [6], что стимулировало развитие способов визуализации и методов компьютерного исследования структуры биомолекул. В 1963 году опубликовали статью, посвященную методу определения генетического родства различных организмов с помощью гибридизации ДНК [17]. На основе этого подхода впоследствии разработали метод ДНК—ДНК гибридизации, который, в свою очередь, стал мощнейшим инструментом молекулярной филогенетики в 1980-е годы.
В 1964 году создали первую электронную систему визуализации молекул [8], что существенно расширило возможности анализа пространственной структуры белков. Спустя три года разработали первую компьютерную программу на основе метода эмпирических силовых полей («фундамент» современной молекулярной динамики), позволяющую рассчитывать потенциальную энергию любых молекул. Тогда же, в 1967 году, сконструировали первый в мире автоматический белковый секвенатор, позволивший устанавливать аминокислотные последовательности белков с невиданной ранее скоростью и точностью [18].
В 1969 году впервые применили подход моделирования структуры белка по гомологии [19]. Тогда модель α-лактальбумина построили из проволоки и пластика на основе структуры лизоцима [20]. В 1970 году предложили первый математический алгоритм выравнивания последовательностей — методическую основу биоинформатики [21]. Кстати, термин «биоинформатика» ввела в 1970 году Полина Хогевег как «изучение информационных процессов в биотических системах» [22], однако его значение со временем трансформировалось (см. предисловие). В 1975 году вышла первая работа по изучению белок—белковых взаимодействий с применением компьютерной техники, посвященная исследованию взаимодействия гемоглобина S в волокнах серповидных эритроцитов [23]. В 1982 году Ирвин Кунитц создал программу DOCK — первый автоматизированный алгоритм для молекулярного докинга [24]. Впоследствии молекулярный докинг стал неотъемлемым подходом, повсеместно применяемым в разработке лекарств [25].
Откуда взялись «большие данные»
Наиболее значимые открытия, определившие направления развития не только структурной биологии, но и биологии в целом, произошли в семидесятых годах двадцатого века. В этот период накопление данных о биомолекулах стало стремительно ускоряться. Уже тогда было известно довольно много аминокислотных и нуклеотидных последовательностей, а также структурных данных о различных белках, поэтому возникла необходимость в их систематизации, развитии способов анализа, сравнения и обмена этими данными, что естественным образом способствовало развитию специализированных баз данных.
В 1971 году Хьелль Клеппе опубликовал статью, в которой предложил подход ферментативной амплификации (копирования) фрагментов ДНК с использованием коротких олигонуклеотидных затравок (праймеров) [32], [33]. Удивительно, но подход оставался без должного внимания вплоть до 1983 года, когда Кэри Мюллис использовал этот принцип для создания метода полимеразной цепной реакции (ПЦР), без которого современная биохимия и медицина просто немыслимы [33], [34]. В частности, ПЦР используется во многих подходах высокопроизводительного секвенирования ДНК [9], [35].
В 1975 году Фредерик Сенгер опубликовал метод прямого ферментативного секвенирования ДНК [36], а уже в 1977 он же представил новый подход, который лежит в основе определения последовательности ДНК современными автоматизированными капиллярными секвенаторами [37], первый из которых создали в 1986 году [38]. Однако еще до этого были полностью расшифрованы довольно протяженные фрагменты ДНК: в 1977 году Сенгер секвенировал геном бактерифага φX-174 (5 386 нуклеотидов), в 1981 секвенировали митохондриальную ДНК человека (16 659 нуклеотидов), а в 1984 — геном вируса Эпштейна-Барр (172 281 нуклеотидов).
Расцвет «текстовой» биоинформатики
Несмотря на то, что методический фундамент биоинформатического анализа последовательностей биополимеров был заложен еще в 1960-х годах пионерскими работами великой Маргарет Дэйхофф (которая, кстати, предложила использовать однобуквенные обозначения аминокислот и еще много чего, что широко используется в «сухой» биологии), масштабное развитие этого направления началось значительно позже.
1990 год можно считать началом очередного этапа развития молекулярной биологии, который характеризуется стремительным накоплением геномной информации. Именно тогда появилась программа BLAST, позволяющая осуществлять очень быстрый и эффективный поиск в базах данных последовательностей [39]. Однако главным событием тогда стало начало реализации «Генома человека» — самого масштабного и амбициозного международного научно-исследовательского проекта за всю историю биологии. Главной целью проекта было определение последовательности нуклеотидов, которые составляют человеческую ДНК, и идентификация генов в человеческом геноме [11]. В 1992 году в Великобритании основали Институт Сенгера (Wellcome Trust Sanger Institute). В том же году Крейг Вентер организовал Институт геномных исследований (The Institute for Genomic Research) в США, а в 1998 году — компанию Celera. Эти организации сыграли огромную роль не только в успешном завершении проекта «Геном человека» (формально завершен в 2000 году, фактически — в 2006), но и стимулировали развитие методов высокопроизводительного секвенирования ДНК [9], [35], что в свою очередь стимулировало развитие методов анализа геномной информации, геномики и биомедицины.
«Сухие» методы
Выравнивание последовательностей
Как отмечено выше, биоинформатика последовательностей занимается изучением нуклеотидных/аминокислотных последовательностей (то есть первичной структуры) основных биополимеров — нуклеиновых кислот (НК) и белков. Такие последовательности принято записывать в виде однобуквенных обозначений (T/U, A, G и C — для обозначения остатков ДНК/РНК (нуклеотидов), и 20 обозначений аминокислотных остатков — для белков). Их сравнительный анализ позволяет [40]:
- соизмерить сходство и установить соответствие между остатками;
- определить консервативные и вариабельные участки;
- высказать соображения об эволюционных взаимосвязях.
О том, чем занимается биоинформатика и где этому можно научиться, более подробно читайте в специальных публикациях на «биомолекуле»: «Я б в биоинформатики пошёл, пусть меня научат!» [4] и «Сome to the bioinformatics side: Институт биоинформатики в Санкт-Петербурге» [41].
Наиболее рутинным подходом в этой области является выравнивание последовательностей — базовый биоинформатический метод, основанный на размещении двух или более последовательностей ДНК, РНК или белков друг под другом таким образом, что можно легко определить сходные/различающиеся участки в этих последовательностях. То есть выравнивание — это определение соответствия между аминокислотными остатками (для белков) или нуклеотидами (для НК) [40].
Как это выглядит. В чем проблема
Вот как это работает. Предположим, есть две последовательности символов: ВООБРАЖЕНИЕ и СОДЕРЖАНИЕ. Принимаем во внимание, что символы в последовательностях переставлять нельзя (поскольку это будут уже другие последовательности).
| Самое простое, но наименее информативное выравнивание выглядит вот так: | Можно попробовать добавить пропуск с другой стороны: | Очевидно, что соответствие в последовательностях будет нагляднее, если добавить пропуск посредине второй последовательности: |
| вОобРажение сОдеРжание- |
воОбраЖеНИЕ -сОдерЖаНИЕ |
вОобРаЖеНИЕ сОдеР-ЖаНИЕ |
Немного усложним задачу. Пусть нашими последовательностями будут GTATAGTCTA и GTTAGTAGTC. Можно попробовать выровнять их.
| Вот так: | Или так: |
| GTaTAGTc-Ta GT-TAGTagTc |
GT-A-TAGTCta GTtAgTAGTC-- |
Однако совершенно не очевидно, какое из этих выравниваний более оптимально (в первом — больше совпадений, но во втором — меньше пропусков). Вообще, количество вариантов выравниваний можно рассчитать с использованием формулы: N = (a + b)! / (a! × b!), где a и b — длины последовательностей. В случае примера, приведенного выше, a = b = 10, a N = 184 756. Если последовательности будут состоять из 20 символов каждая, то N составит уже 1,38 × 1011, а при длине в 100 символов N = 9,05 × 1058. Тут встают два вопроса: во-первых, какое выравнивание считать оптимальным, во-вторых, как его найти среди всех возможных вариантов (ведь очевидно, что простой перебор всех вариантов с использованием существующих вычислительных ресурсов займет годы даже для не очень длинных последовательностей)?
Сравнение сходства последовательностей. Точечные матрицы
Для начала можно представить сравнение последовательностей в виде своеобразной матрицы, в которой строки будут соответствовать остаткам в одной последовательности, а столбцы — остаткам в другой. Если оставить свободными ячейки на пересечении столбцов и строк, где остатки не совпадают, то заполненные ячейки, расположенные на диагонали, отобразят совпадающие фрагменты последовательностей. Такие таблицы называют точечными матрицами сходства последовательностей. Для последовательностей ERWINRUDOLFJOSEFALEXANDERSCHRÖDINGER и ERWINSCHRÖDINGER (полное и короткое имена великого физика Эрвина Шрёдингера) точечная матрица представлена на рисунке 2.

Рисунок 2. Пример точечной матрицы сходства последовательностей и соответствующее оптимальное выравнивание. Самые длинные совпадения, выделенные жирным шрифтом, — первое (ERWIN) и последнее (SCHRÖDINGER) имена. Более короткие фрагменты (ER, IN) являются шумом, как и случайные одиночные совпадения. При движении вправо в вертикальную последовательность в выравнивании вставляется пропуск, а при движении вниз — в горизонтальную; при движении по диагонали пропуски вставлять не нужно — остаток из одной последовательности ставится в соответствие остатку из другой. Движение вверх или влево запрещено, поскольку это приведет к сравнению одного из символов с несколькими из другой последовательности. Путь, указанный стрелками, соответствует очевидному выравниванию внизу рисунка.
рисунок Ольги Пташник
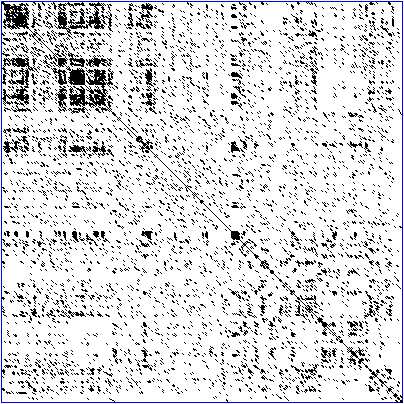
Рисунок 3. Реальная точечная матрица последовательности белка — транскрипционного фактора «цинкового пальца». Непрерывная главная диагональ отражает выравнивание последовательности самой на себя, линии в верхнем левом углу рядом с главной диагональю отражают похожие или повторяющиеся участки последовательности.
Точечная матрица позволяет быстро и наглядно продемонстрировать сходство последовательностей (рис. 2 и 3). Однако сходство «дальнородственных» последовательностей на ней видно плохо. Тем не менее любой путь из ее левого верхнего угла к правому нижнему (если каждый шаг делать либо по диагонали, либо вправо, либо вниз) соответствует возможному выравниванию, что позволяет примерно оценить более-менее оптимальные варианты. Можно воспринимать этот путь как порядок редактирования — серию элементарных операций (замены остатка или вставки пробела), в результате которых горизонтальная последовательность превратится в вертикальную, при том, что каждая из операций соответствует лишь одному шагу по точечной матрице. А минимальное количество таких операций называется редакционным расстоянием. Редакционное расстояние отражает, насколько одна последовательность «не похожа» на другую. Очевидно, что формально задачу выравнивания необходимо свести к определению редакционного расстояния.
Однако само по себе редакционное расстояние не указывает на конкретный оптимальный вариант выравнивания. Для последовательностей GTATAGTCTA и GTTAGTAGTC редакционное расстояние составляет 4, и все же, как отмечено выше, «на глазок» трудно решить какое из двух выравниваний более оптимально. На рисунке 4 показаны порядки редактирования, соответствующие этим выравниваниям.
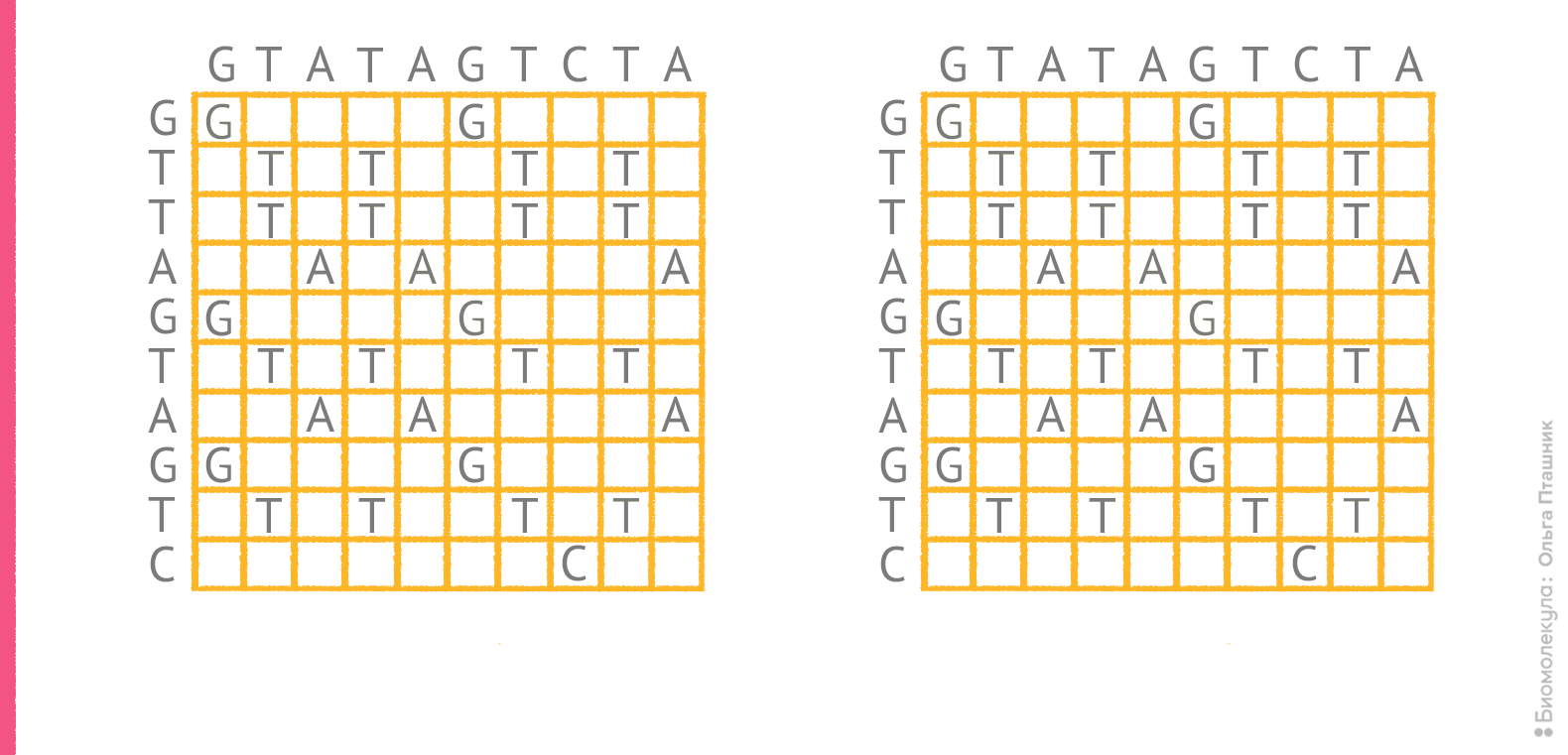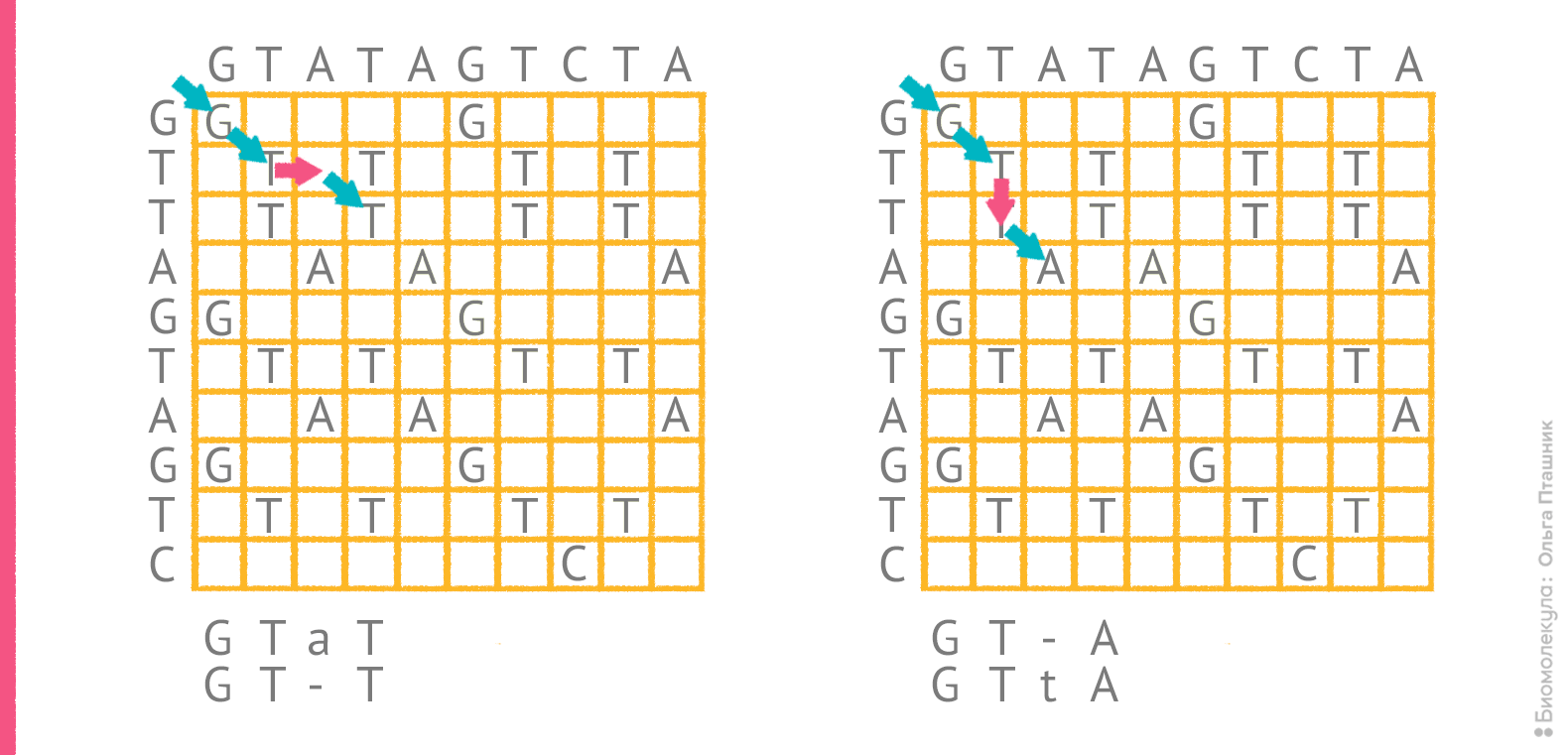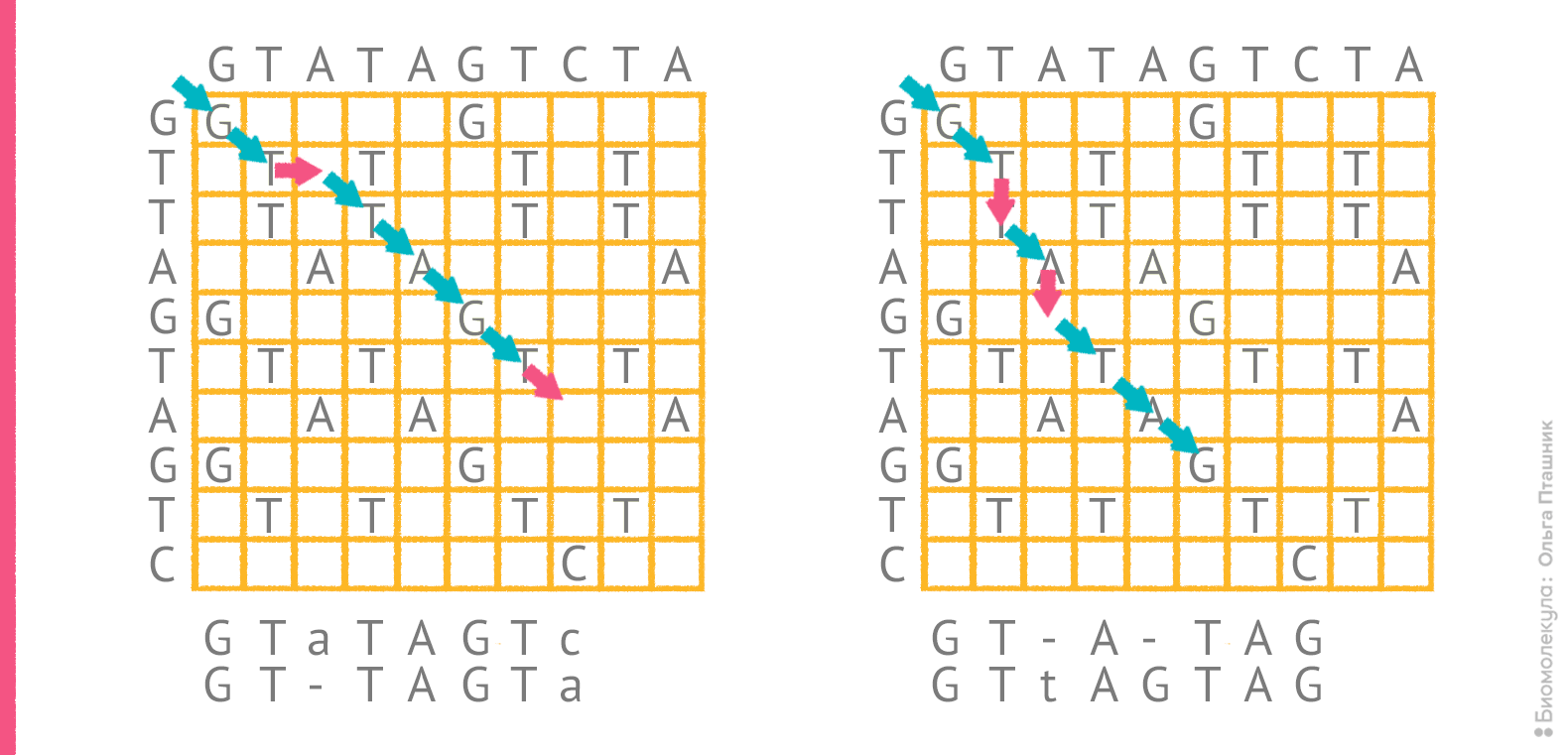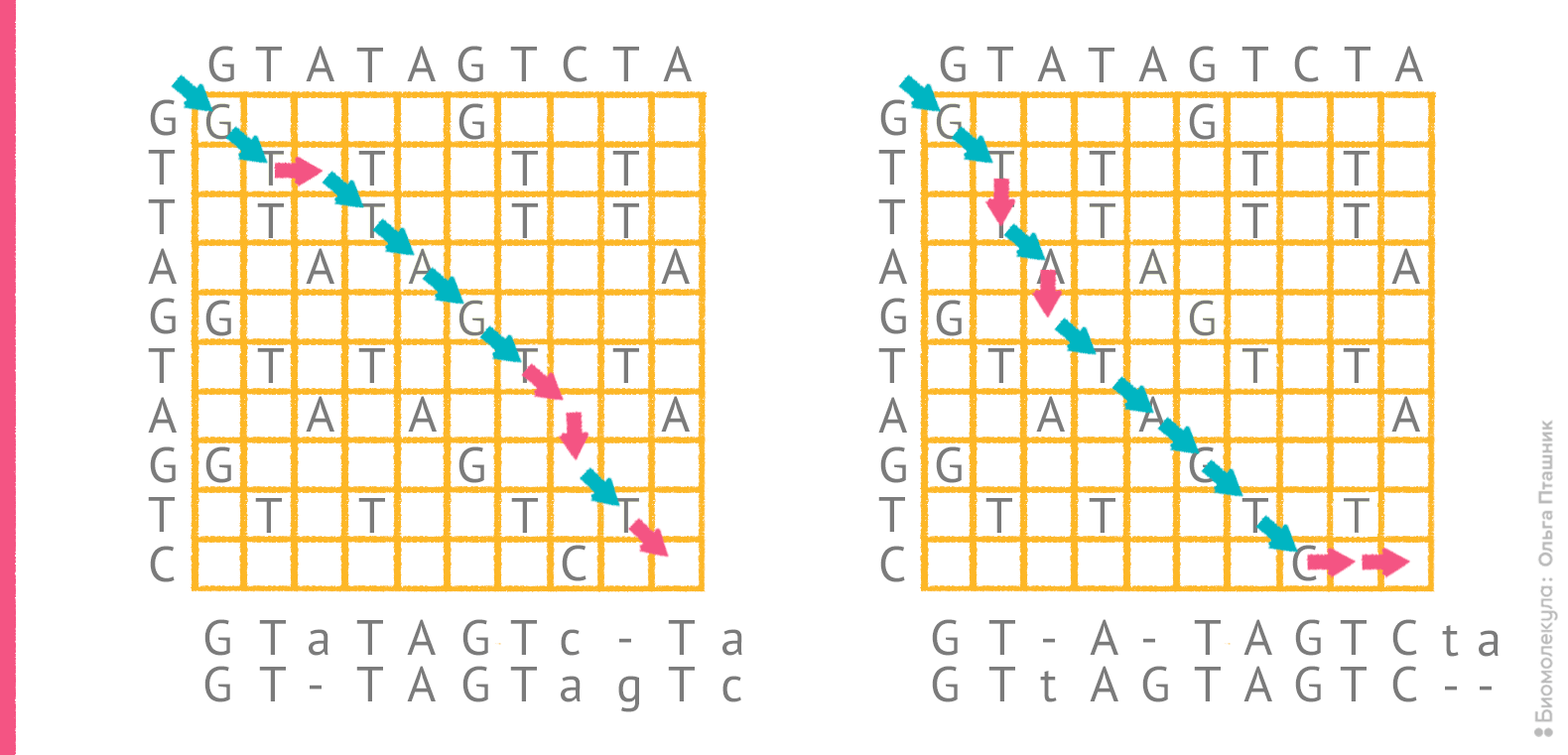
Рисунок 4. Два возможных порядка редактирования для пары последовательностей и соответствующие им выравнивания. Красные стрелки отражают операции, при которых в сопоставление попадают два разных остатка или остаток и пропуск.
рисунок Ольги Пташник
Критерии оценки выравнивания. Матрицы замен
Несложно вывести формулу, по которой можно «взвесить» (оценить), какое выравнивание лучше. Такую формулу называют весовой функцией. В упрощенном виде ее можно представить так: W = (Neq × Keq) + (Nsub × Ksub) + (Nind × Kind), где W — вес выравнивания, Neq, Nsub, Nind — количество совпадений, несовпадений и разрывов (соответственно), а Keq, Ksub, Kind — соответствующие весовые коэффициенты. Если назначить бонус за совпадение остатков в Keq = 1, и штрафы Ksub = −1 (за несовпадение) и Kind = −2 (за разрыв), то наиболее «тяжелое» выравнивание и будет наиболее оптимальным. С такими коэффициентами вес выравнивания для последовательностей GTATAGTCTA и GTTAGTAGTC слева равен 1, а вес выравнивания справа — 0, следовательно, левое выравнивание более оптимально.
Очевидно, что вес выравниваний (а значит и то, какое выравнивание считать оптимальным) сильно зависит от весовых коэффициентов. Существует множество используемых схем присвоения этих коэффициентов. Дело в том, что при выравнивании последовательностей считается, что одна последовательность является «предком» другой, которая получилась из предковой в результате замен, делеций (укорочений) или инсерций (удлинений). В частности, с точки зрения молекулярной эволюции, несколько разрывов, идущих подряд, и такое же их количество, разбросанное по всей длине выравнивания, имеют разный смысл, поэтому их важно различать при построении выравнивания. Многие программы используют не линейные штрафы за разрыв (как в формуле выше: Nind × Kind), а аффинные, то есть K0 + (Nind − 1) × Kind, где K0 — штраф за открытие разрыва, а (Nind − 1) × Kind — штраф за продолжение разрыва). Кроме того, биоинформатика работает с последовательностями, отражающими строение молекул, для которых известно, какие замены происходят чаще, а какие реже. Так, аминокислотные остатки с бóльшей вероятностью заменяются на сходные по свойствам, чем на различные (например, замена V↔I значительно более вероятна, чем V↔R). На основе статистического анализа всех вариантов аминокислотных замен были разработаны матрицы замен — своеобразные таблицы, используемые для присвоения весового коэффициента для каждой конкретной аминокислотной замены с учетом ее вероятности. В настоящее время наиболее популярны матрицы замен BLOSUM и PAM, которые используются практически во всех программах для выравнивания белковых последовательностей. Для выравнивания нуклеотидных последовательностей обычно применяют более «простые» весовые коэффициенты.
Динамическое программирование
Для построения оптимального выравнивания двух последовательностей используют метод динамического программирования [42]. В рамках этого метода считается, что задачу необходимо разбить на конечное число менее сложных подзадач, последовательно решить их и рекурсивно использовать эти решения для решения изначальной задачи. Принцип метода проиллюстрирован на рисунке 5. Вот что это значит для нахождения оптимального выравнивания: от начала до конца сравниваемых последовательностей для каждой пары остатков на основе весов выравнивания трех предыдущих пар остатков находится выравнивание с наибольшим весом, а затем, стартуя от выравнивания конечных остатков, эти веса рекурсивно используются для нахождения такого порядка редактирования, который приводит к тому, что вес выравнивания каждой рассматриваемой пары остатков является наибольшим (рис. 5).

Рисунок 5. Пример работы динамического программирования при выравнивании двух последовательностей. Сначала каждый элемент каждой последовательности выравнивается с элементом, не принадлежащим ни одной из них (естественно, вес таких выравниваний формируется только с использованием весового коэффициента для разрывов). Затем находится вес выравнивания первых двух остатков, как наибольший из возможных весов при переходе от трех предыдущих выровненных элементов. По тому же принципу заполняется вся матрица. Затем матрица «проходится» в обратном порядке от последних двух выровненных элементов таким образом, чтобы на каждом шаге рекурсивно воспроизвести ту из трех операций, в результате которой был получен вес рассматриваемого выравнивания. Зеленые стрелки показывают альтернативный рекурсивный путь по матрице (иногда операция вычисления веса в рассматриваемой ячейке приводит к одинаковому результату для двух или даже сразу трех предыдущих пар выравниваний). Этот пример — реализация самого первого алгоритма выравнивания, предложенного Солом Нидлманом и Кристианом Вуншем в 1970 году, и он подходит для последовательностей, которые похожи по всей длине (глобальное выравнивание) [21]. Позднее, в 1981 году Тэмпл Смит и Майкл Ватерман предложили способ локального выравнивания [43], пригодный для выявления сходных участков последовательностей, которые сходны не по всей длине, а лишь в некоторых участках.
рисунок Ольги Пташник
Множественные выравнивания
При решении задач современной молекулярной биологии зачастую необходимо знать, насколько похожи/различны более чем две последовательности. В таких случаях используют не парное выравнивание, о котором речь шла выше, а множественное (рис. 6). Такое визуальное представление первичных структур белков и НК не только позволяет оценить степень их сходства, но и сделать предположения о том, каким путем шла молекулярная эволюция [44].

Рисунок 6. Пример множественного выравнивания последовательностей. Изображены первые 90 позиций множественного белкового выравнивания на примере рибосомального белка P0 (L10E) из разных организмов. Выравнивание получено с помощью программы ClustalX. Разными цветами в выравниваниях выделяют некоторые (идентчные/гомологичные/консервативные) позиции для удобства визуального восприятия.
Для множественного выравнивания в настоящее время используют разнообразные методы, имеющие свои достоинства и недостатки. Большинство методов выполняет прогрессивное выравнивание, используя эвристические алгоритмы, основанные на множестве парных выравниваний наиболее сходных последовательностей, которые постепенно объединяются для получения одного множественного выравнивания (примеры: Clustal, MAFFT, T-Coffee). Итеративные методы работают подобно прогрессивным, однако при добавлении новых последовательностей в растущее множественное выравнивание исходные выравнивания могут неоднократно перестраиваться (примеры: PRRN/PRRP, MUSCLE, CHAOS+DIALIGN).
Применение выравниваний
Вообще говоря, выравнивание последовательностей как инструмент современной биологической науки используется для двух целей. Во-первых, выравнивания необходимы для получения новых научных знаний. Выше упоминалось, что на основе выравниваний можно устанавливать эволюционные взаимосвязи: выравнивание последовательностей — методический фундамент современной молекулярной филогении и биологической систематики в целом [44]. Кроме того, выравнивания являются алгоритмическим звеном других компьютерных подходов молекулярной биологии, в частности моделирования пространственной структуры белков (чуть подробнее эти методы описаны ниже).
Во-вторых, выравнивания используют для поиска гомологичных (то есть, имеющих единое эволюционное происхождение) молекул — белков или НК — в базах данных. Сегодня репозитории UniProt и GenBank содержат десятки и сотни миллионов последовательностей (разной степени аннотированности), и стандартная логика обычных поисковых машин не подходит для эффективного поиска такого рода информации.
Выравнивания в филогении. Построение деревьев
Современная биологическая систематика для установления родства и систематизации различных биологических видов широко применяет методы, основанные на сравнении и определении сходства структур различных молекул (белков, РНК и ДНК). Этот подход носит название молекулярная филогенетика. Результатом филогенетического анализа является филогенетическое дерево — древовидный граф, отражающий эволюционные взаимосвязи между различными видами, имеющими общего предка (рис. 7). Такие деревья позволяют не только ответить на вопрос «кто кому родня?», но и оценить, кто, от кого и когда произошел, то есть реконструировать эволюцию [44].
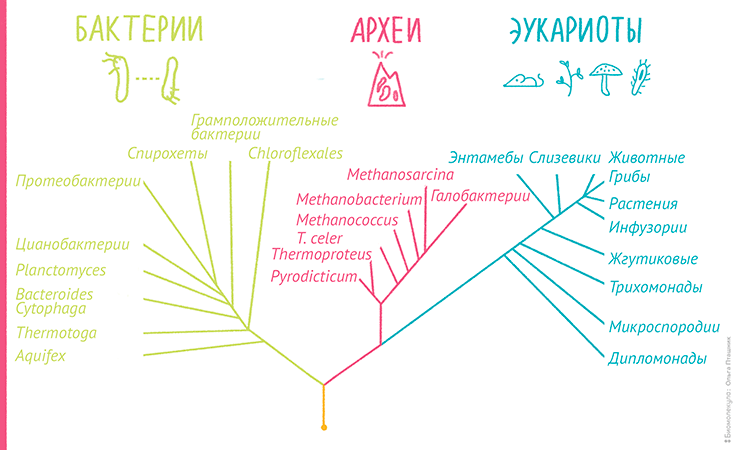
Рисунок 7. Пример филогенетического дерева, построенного на основе сравнения генов рибосомальных РНК, отражающего три домена жизни: бактерии, археи и эукариоты. Кстати, к такому представлению о «родственных взаимосвязях» всех живых существ привела многолетняя кропотливая работа выдающегося американского ученого Карла Вёзе [45].
рисунок Ольги Пташник
Принципиально построение филогенетических деревьев проходит в 4 этапа: создание выборки последовательностей, построение множественного выравнивания, непосредственное построение дерева в виде своеобразной скобочной формулы и визуализация дерева. Несмотря на то, что топология дерева (то есть, количество ветвей и разветвлений, а также их порядок) зависит только от конкретного алгоритма построения, решающее значение имеет качество выравнивания сравниваемых последовательностей, поскольку построить «хорошее» дерево по «плохому» выравниванию просто невозможно.
Использование выравниваний для поиска гомологов
Многие приспособления или изобретения, которые значительно улучшили качество жизни человечества, сегодня кажутся само собой разумеющимися (например, колесо, деньги, лампочка, электронная почта). В науке таких вещей, которые преобразили ее облик и позволили достичь небывалых успехов в развитии технологий и медицины, просто невероятное количество. Их создателей/первооткрывателей стараются отмечать, например, Нобелевскими премиями. Одним из таких изобретений (хотя, вряд ли ее создатели когда-нибудь получат Нобелевскую премию) является программа BLAST (Basic Local Alignment Search Tool) — инструмент для сравнения и поиска последовательностей НК и белков в базах данных.
Логика поиска BLAST достаточно проста. Подобно любой поисковой машине, в BLAST вводится поисковой запрос, представляющий собой исследуемую нуклеотидную или аминокислотную последовательность. Сначала BLAST находит в этой последовательности отдельные «слова» определенной длины (по умолчанию: 3 символа для белков, 11 символов для НК). Затем для каждого слова составляется список похожих слов, имеющих вес при выравнивании с этим словом не менее заданного. Следующий шаг — поиск точного совпадения таких слов в последовательностях базы данных (это занимает немного времени, поскольку все слова заданной длины предварительно занесены в хеш-таблицу — своеобразный указатель того, в какой последовательности и в каком месте встречается каждое слово). Когда соответствие находится, предпринимается попытка «расширить» размеры выравнивания на один символ, затем еще на один — до тех пор, пока вес выравнивания не упадет до порогового значения. Все полученные таким образом выравнивания ранжируются по качеству, и лучшие выводятся пользователю.
BLAST не единственная, не самая быстрая и не самая точная программа в своем роде, но, пожалуй, первая, позволившая выполнять столь качественный поиск в базах данных последовательностей за столь короткое время.
Молекулярное моделирование
Молекулярное моделирование (в широком смысле) — это набор вычислительных методов, позволяющих с разной степенью физической корректности на атомарном уровне изучать молекулярные системы самой разнообразной сложности. Само собой, здесь речь идет о моделировании (то есть, о проведении специфического эксперимента) на компьютере. Кстати, для компьютерного эксперимента существует свой термин — in silico, — что означает буквально «в кремнии» [46]. Сегодня in silico можно смоделировать не только структуру, но и функции биологических молекул, и даже протекание химических реакций. Неудивительно, что Нобелевскую премию по химии в 2013 году вручили Мартину Карплюсу, Майклу Левитту и Арье Варшелю за то, что они заложили фундамент для химического и структурного моделирования биологических молекул [47]. Компьютерным моделированием молекул и их взаимодействий сегодня занимаются два обширных направления, имеющие принципиально разную теоретическую основу: вычислительная химия и собственно молекулярное моделирование.
К вычислительной химии можно отнести все методы, которые используют квантово-механические подходы для расчета свойств и поведения молекулярных систем. Такие подходы в явном виде учитывают строение атома (в частности, электроны и электронные орбитали), в связи с чем требуют огромных вычислительных ресурсов, а также имеют серьезные ограничения по размеру рассчитываемых систем. Обычно квантово-механические расчеты применяют в случаях, когда необходимо рассчитать поведение химических соединений при протекании химических реакций. Такие задачи чаще всего (но не всегда!) относятся к области интересов (био)химии и науки о материалах, а не молекулярной биологии.
Другая группа методов весьма разнородна, однако далее по тексту именно эти методы будут иметься в виду под термином «молекулярное моделирование». Это набор вычислительных подходов, использующих классическую механику, физическую химию и общие представления о химическом строении и физике белка (и других биополимеров) для описания физических свойств атомарных моделей молекул. Соответственно, минимальный неделимый моделируемый объект в таких подходах — атом, хотя степень детализации может быть значительно ниже (например, функциональная группа или аминокислота). Достаточно грубо их можно разделить на несколько ветвей: метод эмпирических силовых полей, методы моделирования структуры по гомологии и молекулярный докинг.
Очень часто моделирование направлено именно на описание (расчет) физических свойств молекулы, а структура при этом слегка «отходит на второй план» (но не теряется там!). В частности, при изучении межмолекулярных взаимодействий, механизмов молекулярного распознавания, особенностей строения конкретных биополимеров и их комплексов, или рациональном конструировании соединений с заданной биологической активностью необходимо учитывать не только геометрию исследуемой системы, но и ее свойства (а точнее, их распределение). Подробнее об этом — в статьях «Роль слабых взаимодействий в биополимерах» [48], «Молекулярная поверхность: что в облике тебе моем?» [49] и «Виртуальные тропы реальных лекарств» [50].
Следует отметить, что существуют подходы к моделированию биологических систем более высокого порядка, позволяющие изучать очень сложные процессы, такие, например, как диффузия или работа клетки целиком [5], [51]. Как правило, уровень детализации изучаемых явлений в этих подходах значительно ниже, чем атом или даже отдельная молекула. Кроме того, к молекулярному моделированию (хотя и с определенными «натяжками») можно отнести структурный анализ биомолекул для, например, исследования природы РНК—белковых взаимодействий и выявления принципов эволюции химических систем в биологические [52]. Однако в этой статье мы не будем подробно останавливаться на этих методах.
Эмпирические силовые поля: что это и для чего
Безусловно, квантовая механика позволяет описать строение молекул и все типы внутримолекулярных (как, впрочем, и межмолекулярных) взаимодействий в явном виде. Однако решение уравнения Шредингера — основного уравнения квантовой механики, — очень сложная задача, практически неразрешимая, когда речь идет о макромолекулах (белки, НК) [53], изучением которых занимается молекулярная биология. Поэтому для описания состояния и расчета динамики макромолекул создали упрощенный подход — молекулярную механику, или метод эмпирических силовых полей.
Идея метода состоит в том, что, вычисляя потенциальную энергию молекулярной системы, можно установить ее динамическое поведение во времени, либо близкую к существующей в природе пространственную структуру. В рамках метода молекула рассматривается как набор частиц, причем каждая пара частиц взаимодействует по известным физическим законам. Энергия взаимодействия каждой пары частиц представляется как сумма энергий различных типов взаимодействий: ковалентных, электростатических, вандерваальсовых и др. (рис. 8). При этом параметры, характеризующие все взаимодействия этих частиц (например, массы, длины валентных связей, вандерваальсовы радиусы, парциальные заряды, валентные и торсионные углы и т.д.), подбирают эмпирически (из условия самосогласованности теоретических и экспериментальных характеристик системы). Набор всех этих параметров и называют эмпирическим силовым полем.
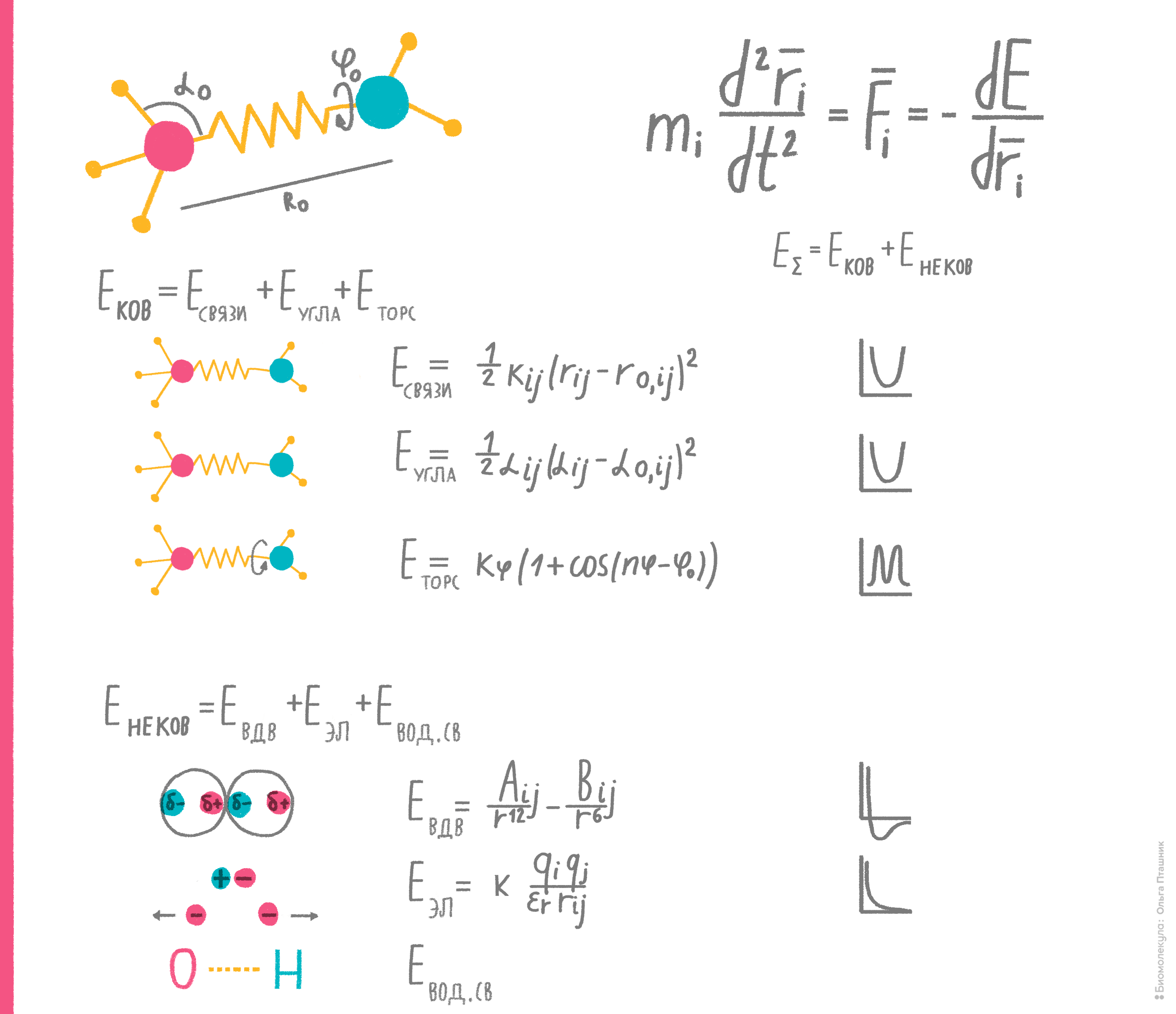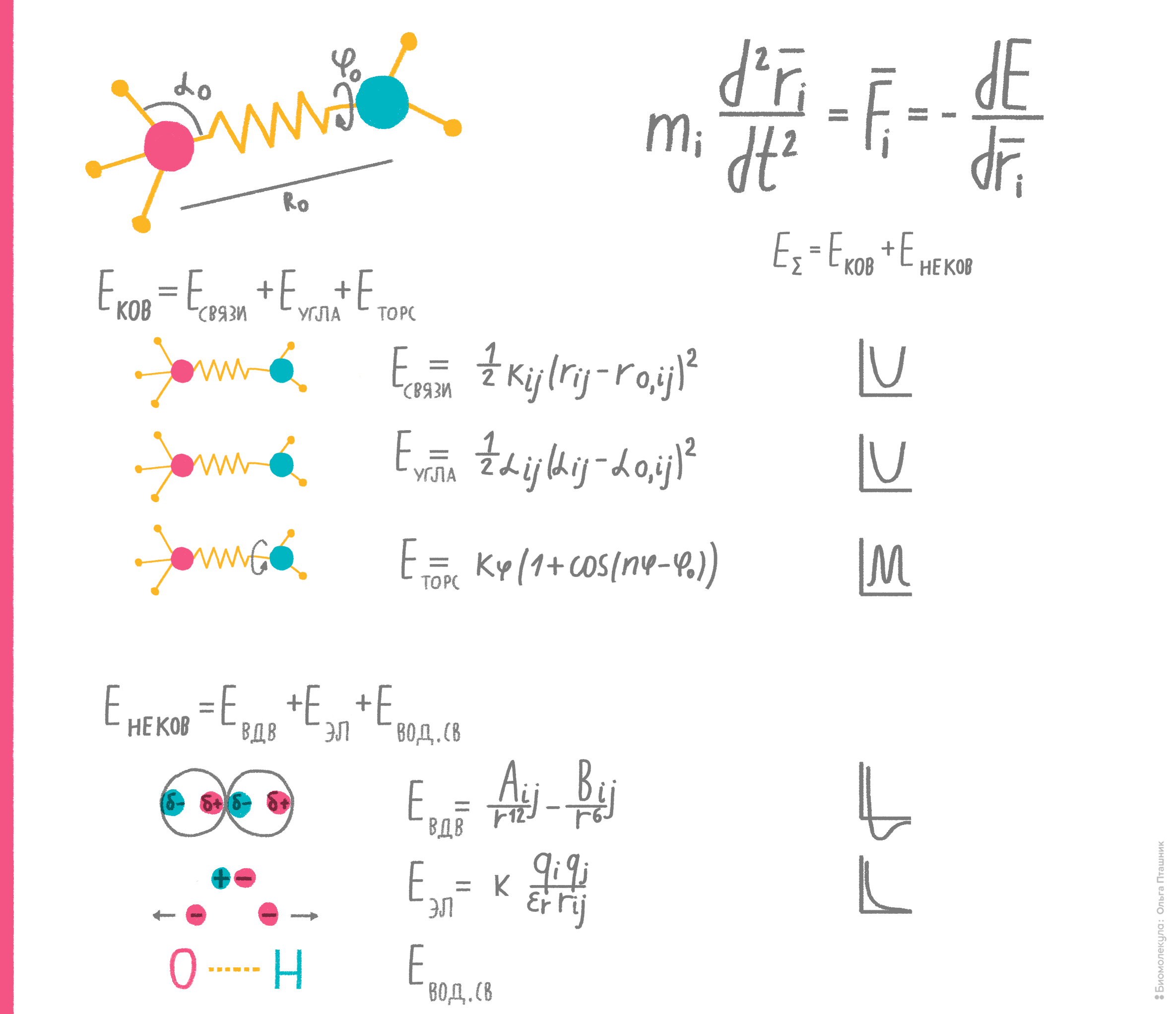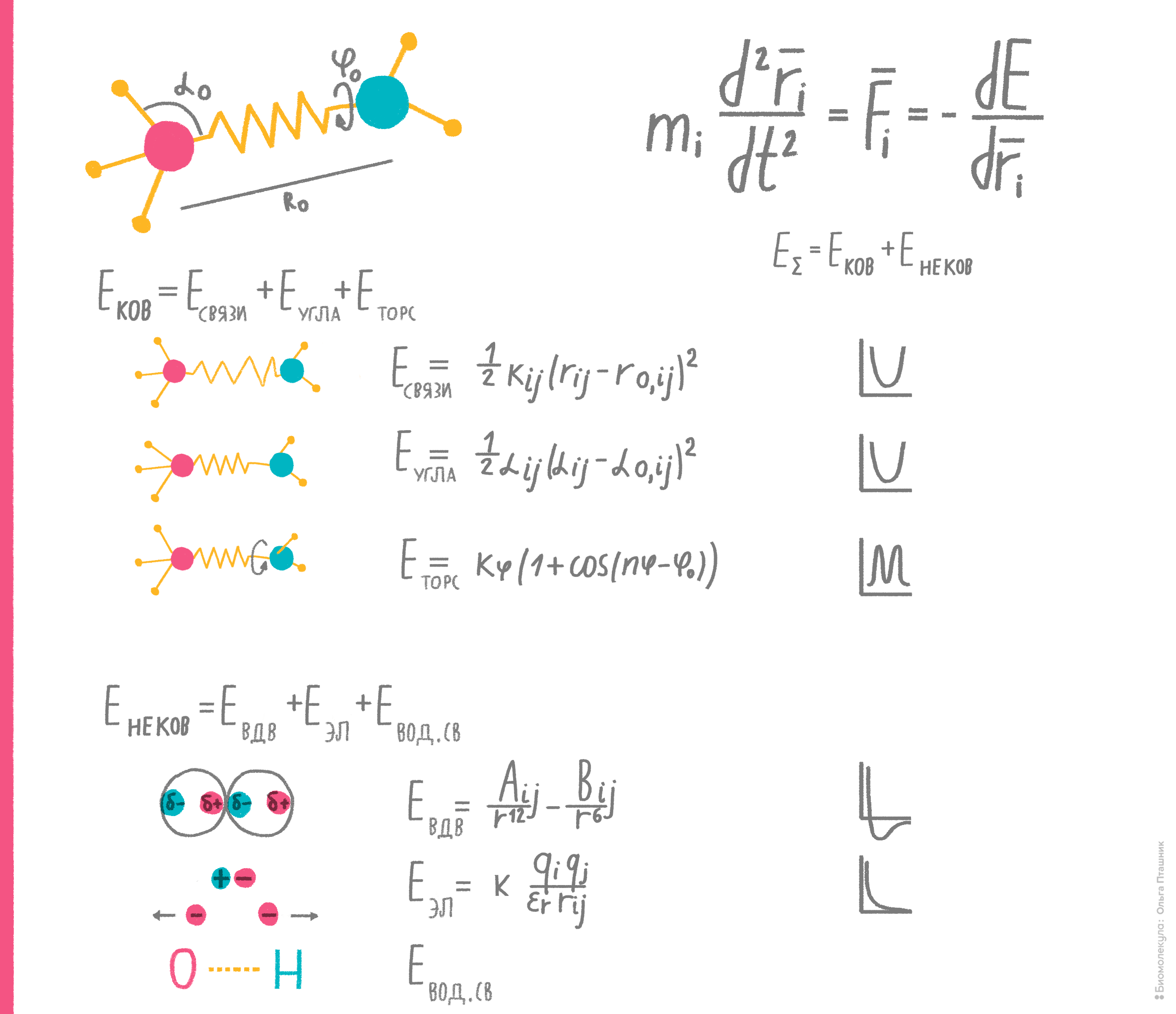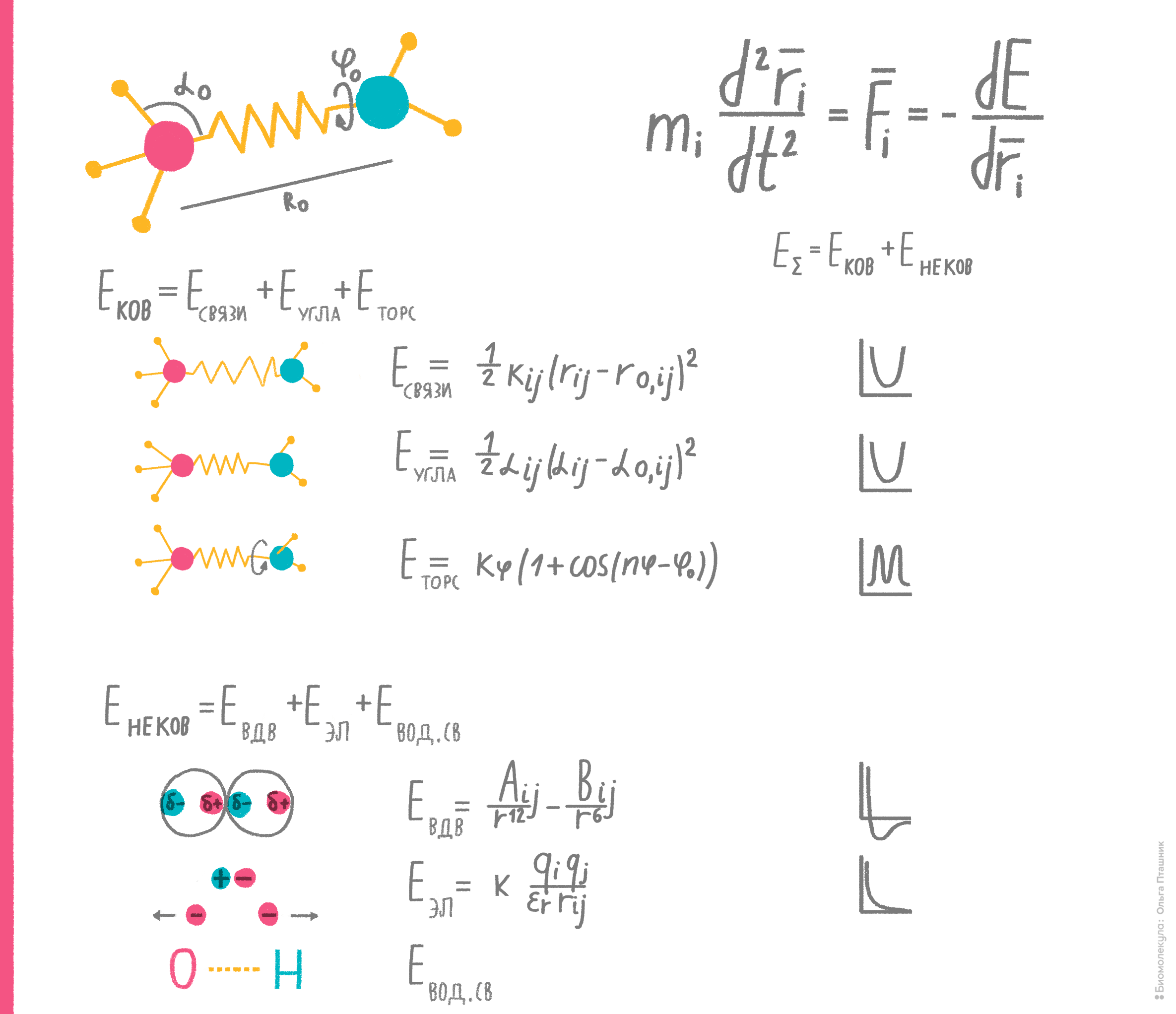
Рисунок 8. Физико-математическая основа самосогласованных силовых полей. Если учесть все типы взаимодействий частицы (атома) и вычислить энергию каждого из них, подставив соответствующие константы в каждое из уравнений, то сумма результатов покажет полную потенциальную энергию. А если проследить изменение этой энергии при движении частицы, то можно вычислить ее ускорение, а значит, и скорость, и относительное положение в пространстве в каждый конкретный момент времени... И наоборот. А взаимное расположение в пространстве химически связанных атомов — это и есть структура молекулы. На этих нехитрых идеях и основан метод эмпирических силовых полей.
рисунок Ольги Пташник
Метод эмпирических силовых полей, как было сказано выше, дает возможность довольно точно (с определенными ограничениями [19]) рассчитать пространственную структуру макромолекулы, что значительно расширяет возможности структурного анализа биомолекул. А корректное представление о строении молекулы, в свою очередь, дает возможность анализировать физические свойства ее поверхности [49], которые по большей части и определяют ее биологическую активность, а также изучать межмолекулярные взаимодействия.
В настоящее время для разных целей применяют довольно много разных силовых полей. Одни поля лучше оптимизированы для расчета молекулярных систем, преимущественно содержащих белки и НК, другие — для липидов, третьи — для низкомолекулярных соединений, а для физических систем, в которых не имеет смысла детализация до моделей отдельных молекул, силовые поля отличаются еще больше. Кроме того силовые поля можно классифицировать по степени детализации самих параметров. Полноатомные (all-atom) силовые поля содержат параметры для каждого типа атома в системе, включая водород, в то время как поля «объединенных атомов» (united atom) учитывают каждую метильную группу и каждый метиленовый мостик как один центр взаимодействия. Крупнозернистые (coarse-grained) поля, которые обычно используют для моделирования больших молекулярных систем (например, большие мембранные белки в липидном бислое, или многокомпонентные комплексы белков с нуклеиновыми кислотами), содержат еще более обобщенные параметры, объединяющие несколько атомов или даже мелких молекул в единый центр со своими эмпирическими свойствами для повышения эффективности вычислений.
Молекулярная динамика
Движение частицы в составе молекулы можно рассматривать как движение частицы во внешнем поле сил. Со школьной скамьи мы знаем, что такие вещи описываются простым уравнением, известным как второй закон Ньютона. Численное решение этого уравнения позволяет изучить динамику молекулы во времени [7], [53]. Проще говоря, если мы знаем законы, по которым двигаются атомы в молекуле (а мы их знаем — см. рис. 8), если мы знаем все константы для этих атомов, составляющие силовое поле (их мы тоже знаем — они установлены экспериментально или подобраны эмпирически), и если мы зададим взаимное расположение атомов в какой-то начальный момент времени, то мы можем рассчитать их взаимное расположение через какой-то отрезок времени, то есть мы можем рассчитать траектории их движения, а, следовательно, и общую молекулярную траекторию и конформацию молекулы. Компьютерный эксперимент, в котором все это проделывается, называется молекулярная динамика (МД).
Фактически, в МД моделируют различные ансамбли — состояния, в которых микроскопические параметры могут быть произвольными, а макроскопическое состояние удовлетворяет заданным условиям (постоянный объем, температура, плотность и т.д.). Как отмечено выше, результатом такого эксперимента является траектория — файл, содержащий координаты и скорости атомов через равные промежутки времени. Причем эти промежутки должны быть очень маленькие, поскольку для адекватного расчета изменения молекулярной системы во времени шаг МД не должен превышать характерных времен колебания химических связей: ≈10−15 c — фемтосекунда.
МД — один из мощнейших подходов современной компьютерной биологии. С использованием данного подхода удается изучить и визуализировать, как работают большие (например ионный канал в клеточной мембране [54]) и даже очень большие (например вирусный капсид целиком [55]; см. видео 1) молекулярные системы.
Видео 1. Молекулярная динамика полного капсида вируса иммунодефицита человека. Флуктуации поверхности капсида ВИЧ-1 в диапазоне от −3 до +3 Å (от красного до синего), наблюдаемые в процессе молекулярно-динамического эксперимента.
Периодические граничные условия
Однако величина молекулярной системы здесь — штука относительная. В одном моле содержится примерно 6,02 × 1023 атомов, но никакой существующий компьютер не осилит такое количество расчетов. Поэтому в молекулярной динамике редко исследуют системы размером более одного миллиона атомов. Кстати такое количество атомов занимает довольно скромную область пространства — если поместить их в кубическую ячейку, то длина ее ребра составит всего около 20 нанометров. Внутрь такой ячейки легко помещаются большие белки или фрагменты клеточной мембраны, а также ионы и молекулы воды (которые обычно добавляют при моделировании динамики реальных биомолекул).
Но в то же время очевидно, что такая ячейка легко разлетится в окружающем ее «компьютерном вакууме», если ее компоненты никак не удерживать. Для этого существует специальный алгоритм, который называется периодические граничные условия. Суть алгоритма достаточно проста: со всех сторон рассчитываемой ячейки создаются ее виртуальные клоны (в случае кубической ячейки генерируют 26 виртуальных ячеек вокруг одной реальной). Идея в том, что учитывают лишь взаимодействия частиц внутри реальной ячейки, а также их взаимодействия с частицами ячеек-клонов, но внутри этих клонов взаимодействий уже нет. Такой подход, во-первых, ускоряет расчет, во-вторых, предотвращает разлетание компонентов молекулярной системы в пространстве, поскольку, если молекула (или ее часть), «выезжает» за границу ячейки c одной стороны, то она одновременно «въезжает» с другой (рис. 9).
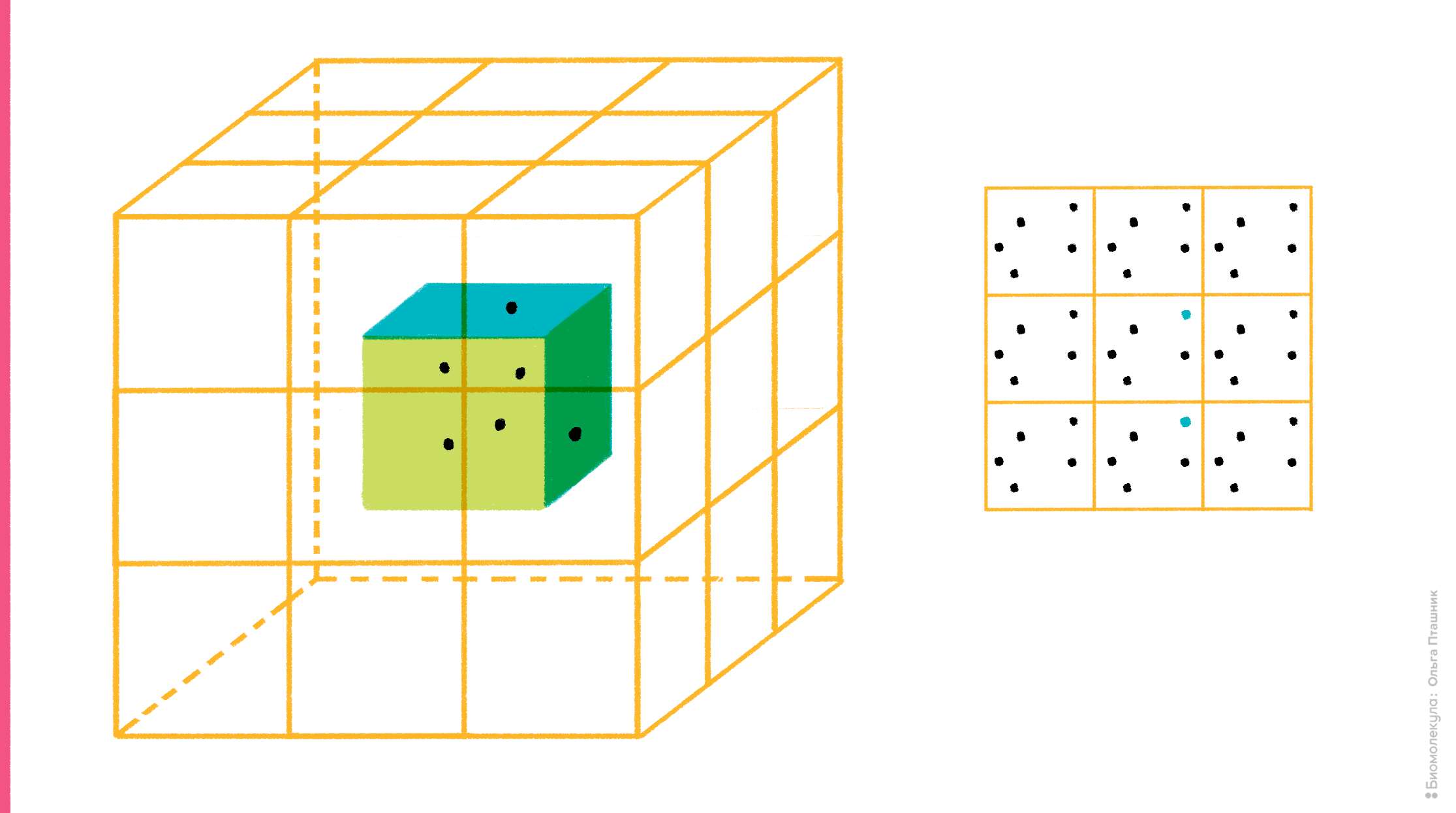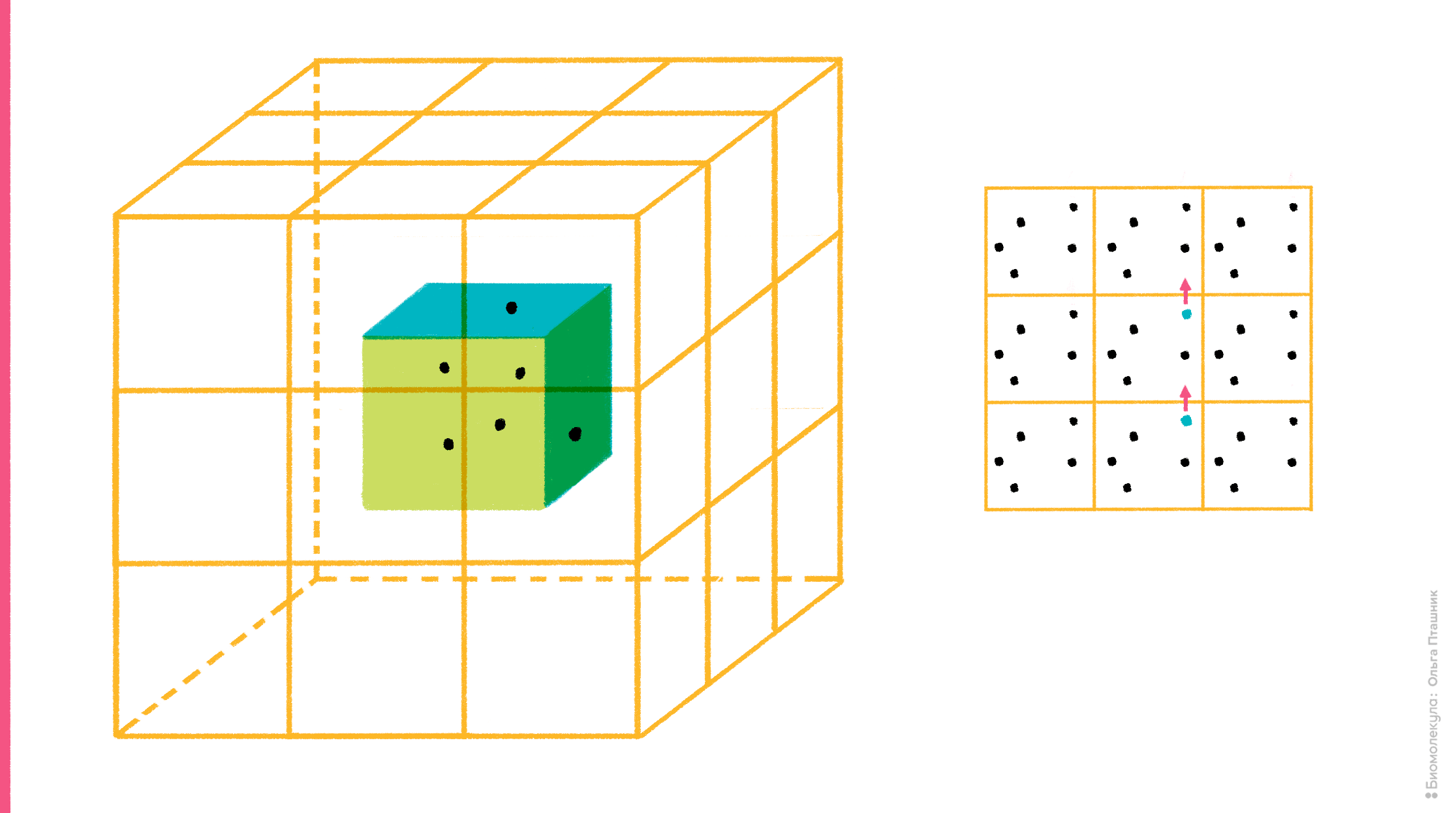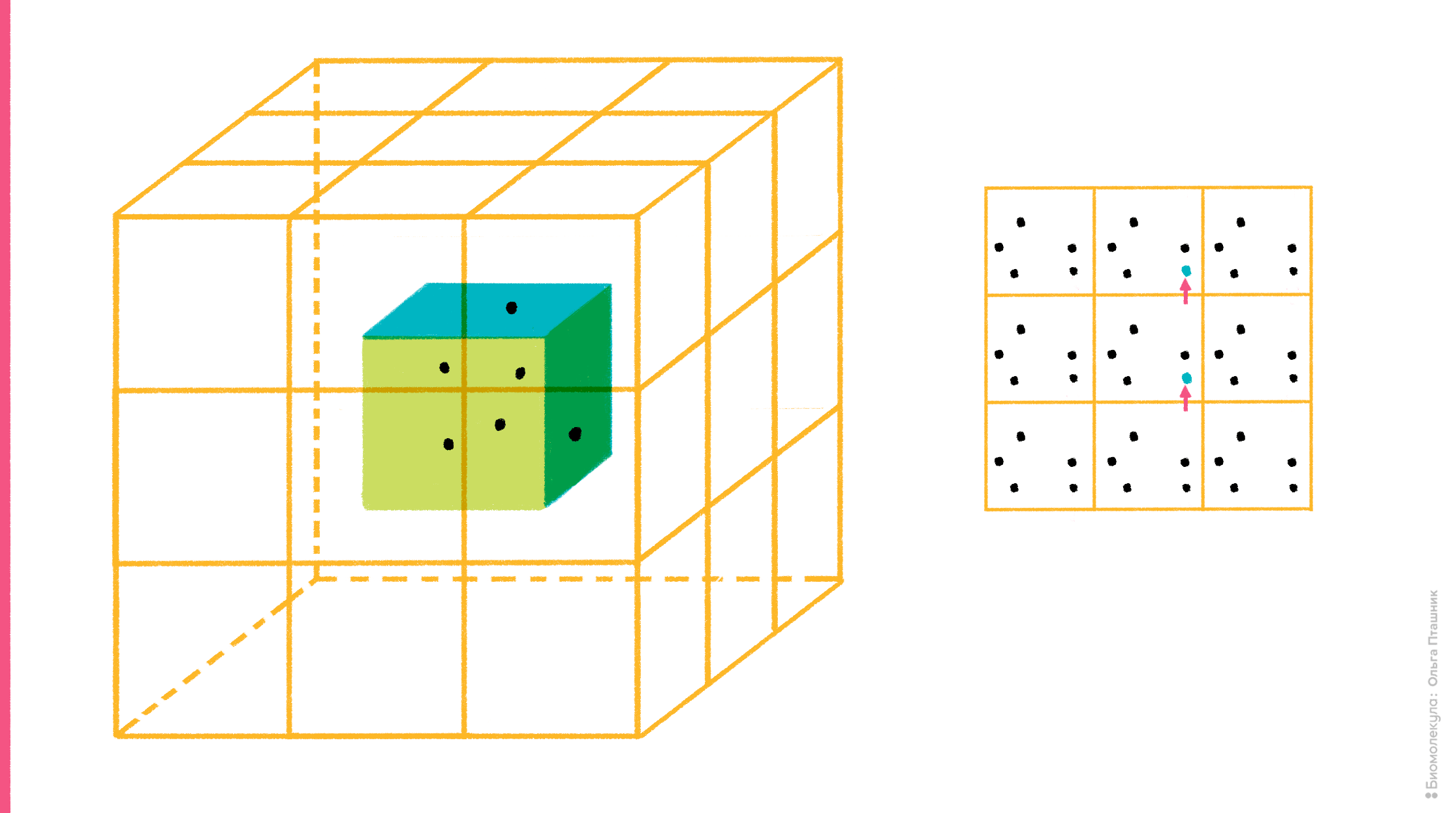
Рисунок 9. Суть алгоритма периодических граничных условий. На рисунке (слева) показана реальная рассчитываемая ячейка, вокруг которой ее виртуальные клоны. Справа показан «переброс» молекулы, когда она «выезжает» за границу ячейки.
рисунок Ольги Пташник
Постоянство термодинамических параметров
Кроме целостности системы, в молекулярной динамике необходимо поддерживать неизменными некоторые макроскопические (термодинамические) параметры, такие как температура, давление и др. Температура здесь определяется исключительно по средней кинетической энергии частиц (кстати, реальная температура тоже) и фактически зависит от их скоростей. Для поддержания постоянной температуры в уравнение движения (рис. 8) добавляют силу, которая пропорциональна скорости движения частицы (аналог вязкого трения). Этот алгоритм контролирует постоянство суммарной кинетической энергии частиц в системе и называется термостат. Подобный алгоритм, контролирующий постоянство давления, называется баростат.
Минимизация свободной энергии
Итак, в силовых полях записаны все константы, определяющие то, как частицы взаимодействуют друг с другом. Имея данные параметры, можно записать математическое выражение для функции потенциальной энергии, которая, как известно, характеризует поведение молекулы (ее структуру и динамику). Самое простое, что можно сделать с использованием такого выражения для энергии — это минимизация свободной энергии, — компьютерный эксперимент, предназначенный в первую очередь для оптимизации геометрии молекулы (видео 2).
Видео 2. Возможное и невозможное в компьютерном моделировании.
Согласно современным представлениям, любая система (как в макро-, так и в микромире) стремится к минимуму энергии (это постулируется, например, вторым началом термодинамики). Следовательно, любая реально существующая молекула находится в энергетическом минимуме, которому соответствует определенная геометрия (взаимное расположение атомов в пространстве) — конформация, или набор конформаций с примерно одинаковой потенциальной энергией. Так вот, эксперимент по минимизации энергии как раз старается найти именно такую конформацию, меняя взаимное расположение атомов в молекуле (за счет вращения вокруг валентных связей) и пересчитывая потенциальную энергию для получившейся конформации.
Минимизация энергии как встроенная функция сегодня есть практически в любом, даже самом незамысловатом программном обеспечении для молекулярного моделирования. С помощью этого метода легко можно избавиться от грубых нарушений геометрии (например, наталкиваний атомов друг на друга, пространственной близости одноименных зарядов, нереалистичных торсионных углов и т.п.), значительно повышающих энергию системы, то есть найти локальные энергетические минимумы. Однако для поиска глобального минимума обычно применяют другие методы.
Метод Монте-Карло
Большинство алгоритмов минимизации энергии представляют собой цепочку пошаговых операций изменения конформации и пересчета потенциальной энергии. Однако такой подход малоэффективен при поиске глобального энергетического минимума молекулярной системы, поскольку он, как правило, «застревает» в локальном, не имея возможности преодолеть потенциальный барьер.
Для того чтобы понять сложность этой задачи, можно сравнить ее с поиском самой нижней точки на поверхности Земли. Уже давно известно, что она находится в Марианской впадине, но человечеству потребовались сотни лет, усилия тысяч людей, и сложное оборудование, чтобы это выяснить. Однако если представить, что некий человек этого не знает и находится, например, в Москве, в его арсенале имеется альтиметр, лот и, скажем, велосипед, то скоро ли он найдет ее, исследуя каждый квадратный метр? Скорее всего, никогда. Так вот функция потенциальной энергии биомакромолекул (белков и НК) значительно сложнее поверхности земли, она имеет огромное количество локальных энергетических минимумов и максимумов (и соответствующих им конформаций), и исследовать все их просто невозможно.
Метод Монте-Карло не исследует все возможные конформации молекул, но вместо этого пытается «совершить путешествие» по поверхности функции потенциальной энергии с тем, чтобы найти низкоэнергетические состояния (видео 2). Для того чтобы не «застрять» в локальном минимуме, ошибочно приняв его за глобальный, в методе предусмотрен алгоритм продолжения поиска. Вот как это работает.
В рамках метода Монте-Карло производится случайное изменение конформации молекулы (например, какого-нибудь торсионного угла) и расчет потенциальной энергии получившейся конформации. Если энергия становится ниже, то конформация запоминается и используется для последующего шага изменения и пересчета потенциальной энергии. Если же энергия становится выше, то такая конформация тоже может быть принята для последующих вычислений с определенной вероятностью, которая пропорциональна разности энергии текущей и предшествующей конформаций. Если эта вероятность выше некой случайной вероятности, то текущая конформация принимается для дальнейших шагов поиска (рис. 10). Процедура сравнения со случайной вероятностью напоминает игру в казино, когда бросают игральные кости, что и дало название методу [7], [15].
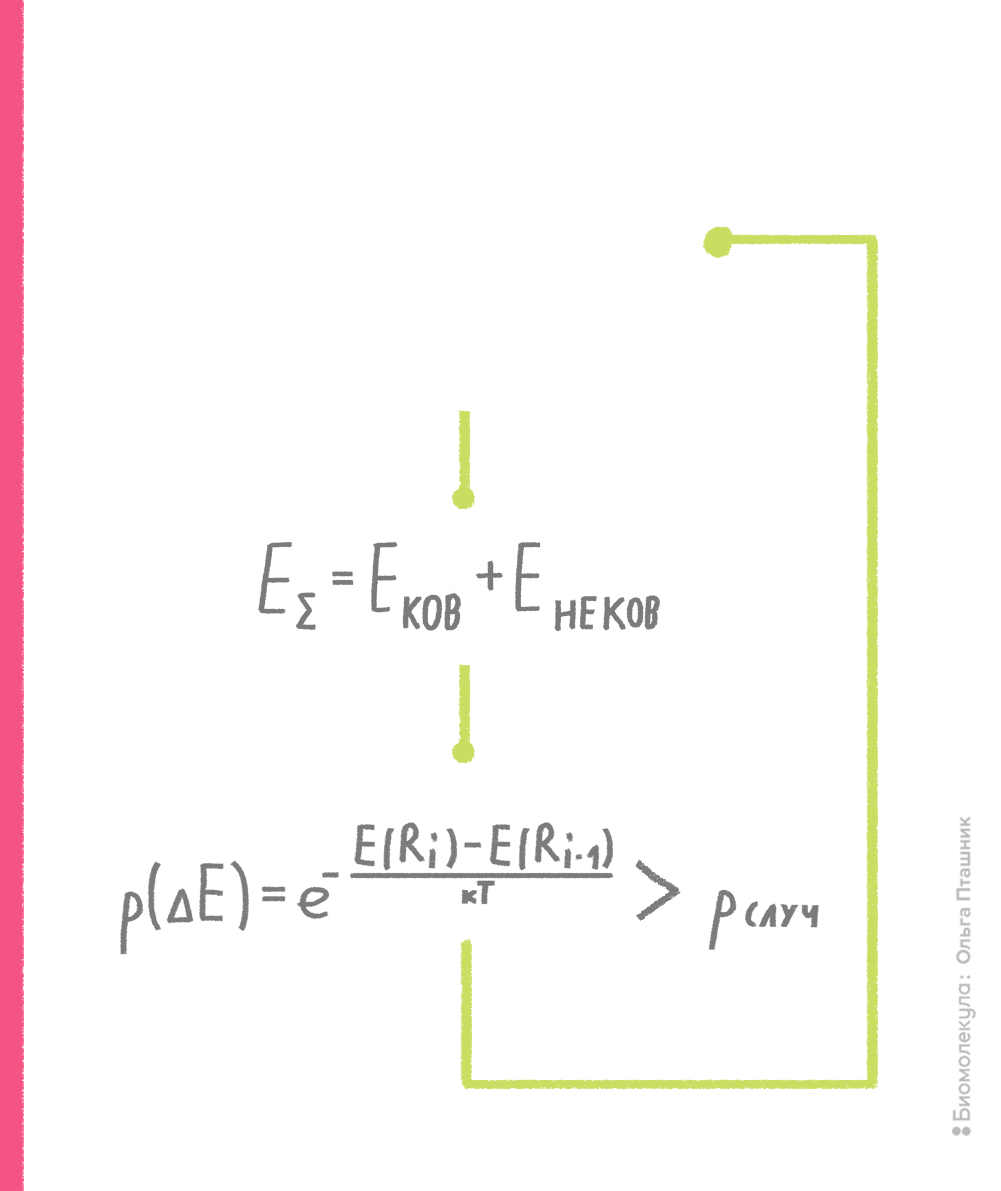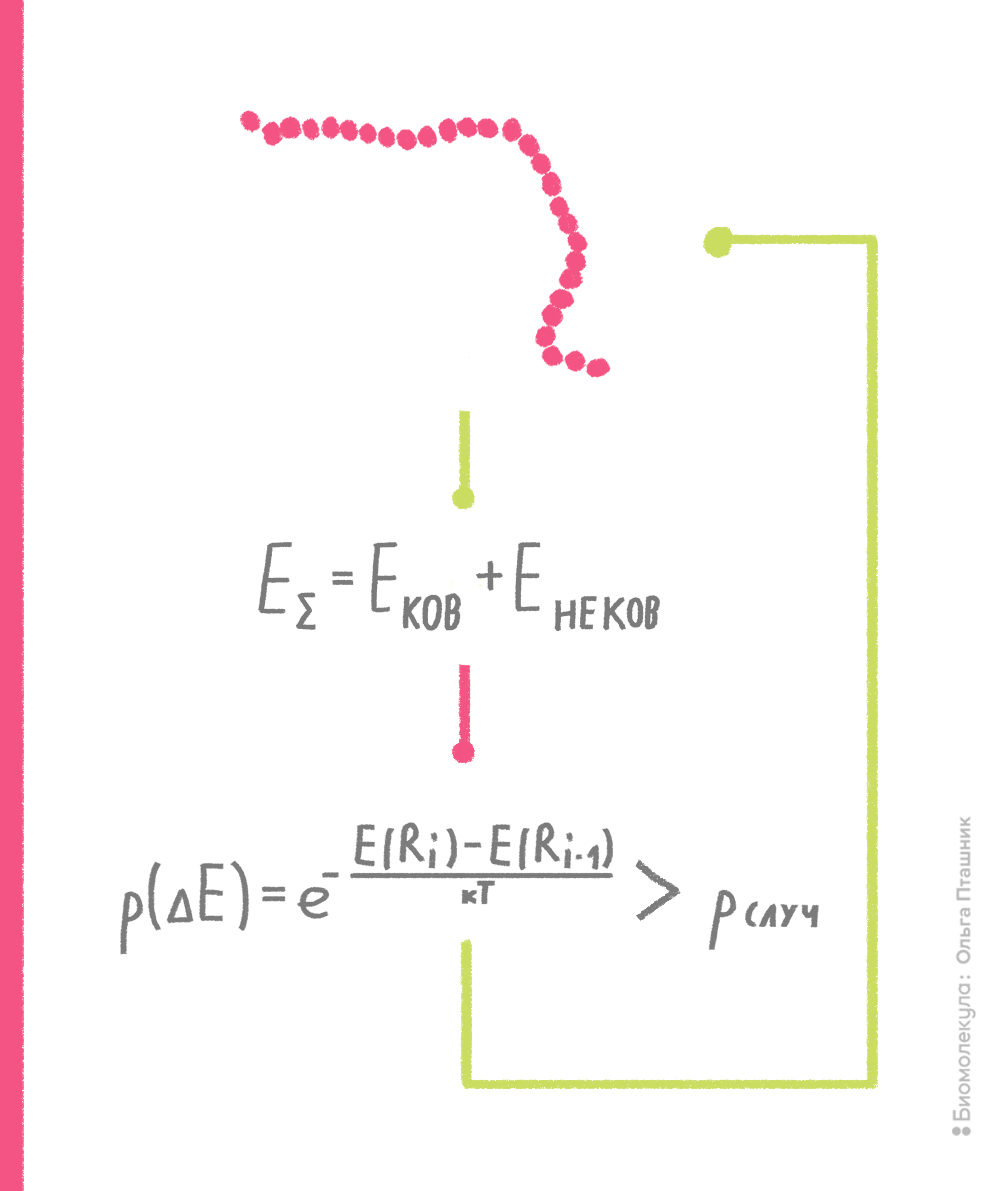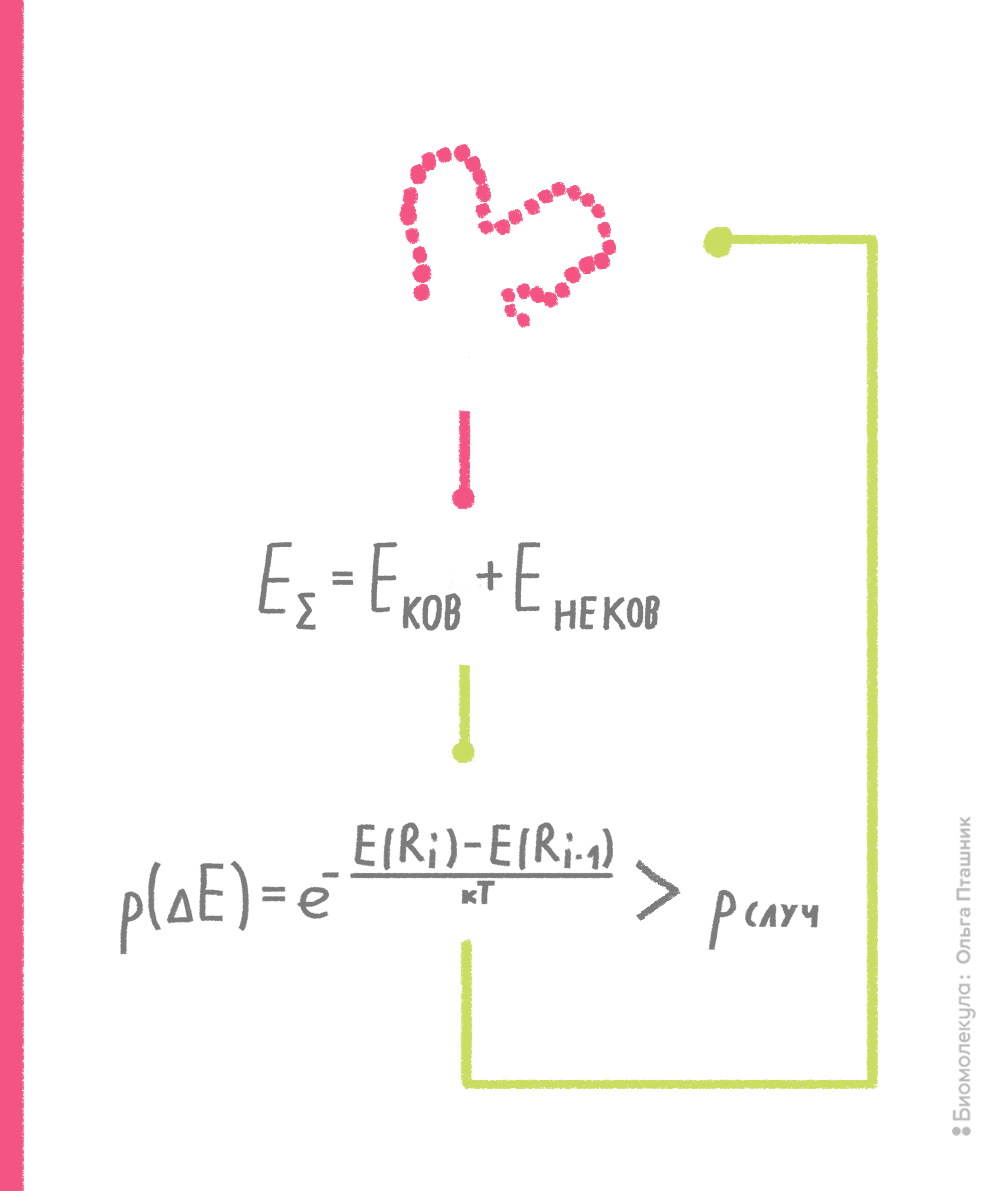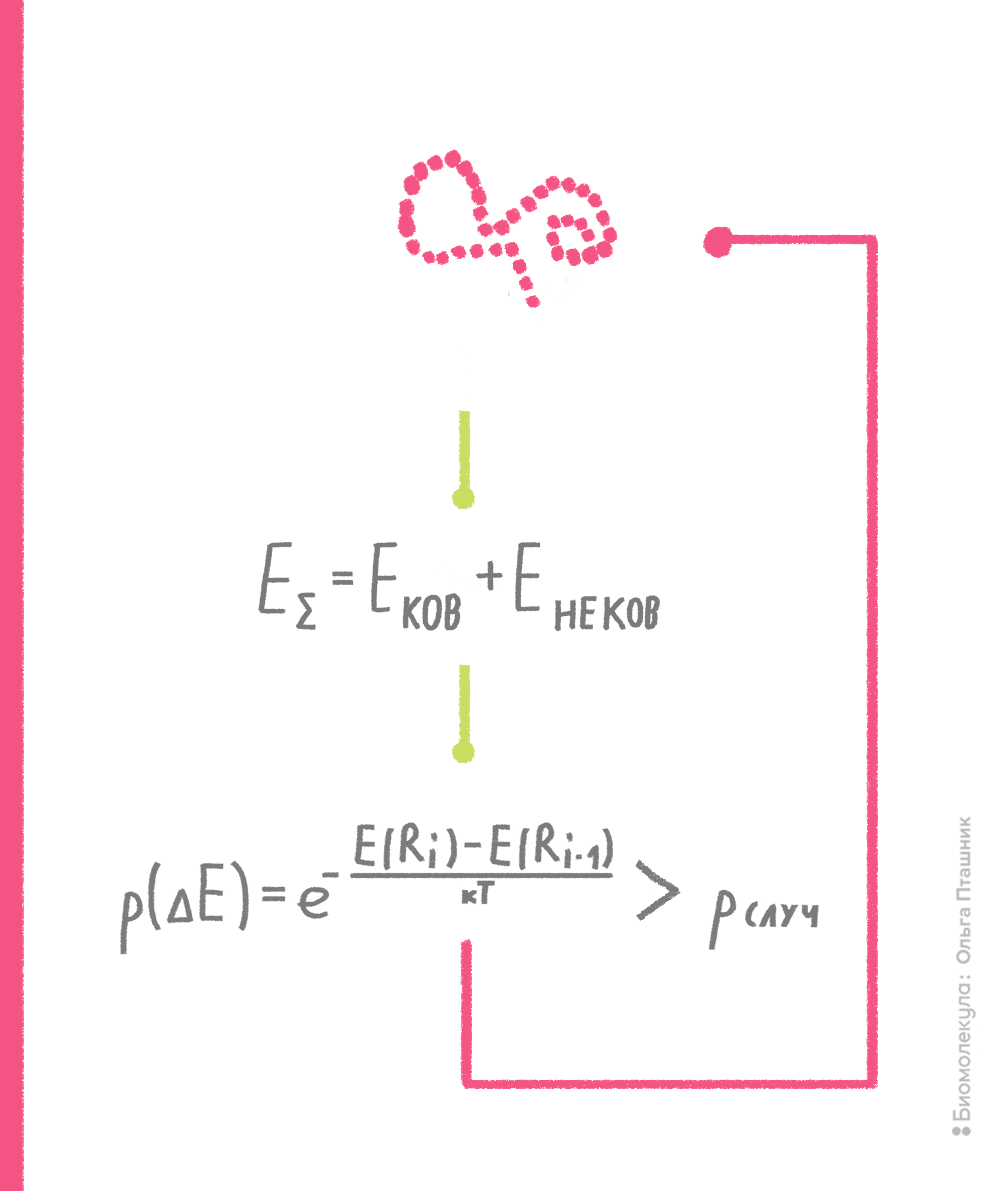
Рисунок 10. Принцип метода Монте-Карло. Нижний блок, отражающий процедуру сравнения вероятностей, называют критерием Метрополиса — в честь создателя метода Николаса Метрóполиса.
рисунок Ольги Пташник
Иногда расчеты с помощью такого подхода называют динамикой Монте-Карло. Однако, в отличие от молекулярной динамики, Монте-Карло не дает динамической картины поведения молекулярной системы, поскольку в этом типе эксперимента не существует такого понятия, как «время»: накапливаемые конформации не связаны друг с другом, каждая последующая конформация случайна по отношению к предыдущей. Кроме того, длительность моделирования для получения представительной выборки «хороших» конформаций нелинейно зависит от размера молекулы. Тем не менее, данный подход позволяет широко представить конформационное пространство исследуемой молекулярной системы, то есть выяснить, какие конформации молекула может принимать с большой вероятностью.
Моделирование пространственной структуры
Если нам известно, как что-то устроено, мы можем понять, как оно работает. Утверждения такого характера справедливы для всех областей интересов человечества, и молекулярная биология не исключение. Знание пространственной структуры молекул, составляющих живые организмы, является необходимым (но, к сожалению, не достаточным) условием для выяснения принципов их функционирования. Именно поэтому так важна структурная биология и ее достижения [6]. Но в ситуации, когда пространственная структура интересующей нас биомолекулы неизвестна, или пока не может быть установлена экспериментально, можно построить ее компьютерную модель на основе уже имеющихся данных.
Следует подчеркнуть, что модель (не только молекулярная, но вообще любая) является абстракцией, используемой для описания реальной системы. Поэтому необходимо понимать и помнить, что корректность выводов, сделанных с использованием модели, зависит от ее качества, которое, чаще всего, чрезвычайно сложно оценить. Нельзя воспринимать модель, как «истину в последней инстанции»!
Проблема фолдинга
Моделирование пространственной структуры белков и НК — задача не из простых. И вот в чем сложность. Из школьного курса биологии мы знаем, что большинство белков имеет три уровня структурной организации: первичная, вторичная и третичная структуры. Фактически белок, или пептид, может выполнять свою биологическую функцию тогда (и только тогда!), когда он имеет «правильную» (нативную) третичную, то есть пространственную структуру, которую на научном жаргоне принято называть фолдом (от англ. fold — клубок). Процесс, при котором белки принимают правильный фолд (фолдинг), происходит во время или сразу после синтеза на рибосоме [56], [57]. В течение фолдинга происходит не только генерация вторичной структуры белка, но и правильная ориентация всех упорядоченных и неупорядоченных участков молекулы друг относительно друга. Иными словами, происходит высокоточная настройка всех торсионных углов. А торсионных углов в белках сотни и тысячи, поэтому существует колоссальное число вариантов сворачивания одной и той же белковой молекулы, из которых лишь один является правильным . Именно его и пытаются найти/предсказать/рассчитать методы моделирования пространственной структуры. В данной статье основные подходы этой группы рассматриваются лишь обзорно, более детальную информацию можно найти в статье «Торжество компьютерных методов: предсказание строения белков» [19].
На самом деле, нативная конформация не одна, а одно «семейство» — группа близких конформаций. Иногда, таких семейств для одного и того же белка может быть несколько [58], [59], а порой даже много [60], [61]. В связи с этим необходимо учитывать как можно больше экспериментальных данных о моделируемом белке, чтобы не тратить время впустую в поисках артефактов.
Моделирование по гомологии
Наиболее распространенным и надежным методом моделирования пространственной структуры белков на сегодняшний день является моделирование по гомологии. Существует множество разнообразных модификаций данного подхода. При использовании некоторых программ для моделирования по гомологии каждый этап приходится делать «вручную» (например MODELLER), в других программах абсолютно все делается автоматически (например SWISS-MODEL). Однако все они базируются на одной и той же идее: предсказание пространственной структуры полипептида на основе сравнения его аминокислотной последовательности с последовательностью прототипа (шаблона), для которого пространственная структура уже известна.
Реализуется это следующим образом. Сначала для интересующего нас белка нужно найти гомолог-шаблон (или несколько), структура которого известна, то есть занесена в PDB. Затем необходимо построить выравнивание последовательностей шаблона и целевого белка, чтобы на следующем шаге программе было понятно, какие участки структуры можно просто скопировать, а какие все-таки придется достраивать. Этап построения модели заключается в «натягивании» последовательности моделируемого белка на молекулярный остов шаблона согласно выравниванию. Участки, не имеющие гомологии с шаблоном, достраиваются независимо, а геометрия результирующей модели оптимизируется с помощью метода эмпирических силовых полей. Заключительный этап метода — оценка качества полученной модели с помощью полуэмпирических алгоритмов (это делает компьютерная программа) и с учетом всей доступной экспериментальной информации об этом белке (а вот тут без человека уже не обойтись) [19].
Моделирование de novo
Принципиально другие подходы создания компьютерной молекулярной модели белка — без какого-либо шаблона, — принято называть моделированием de novo (лат. «с начала»). Большинство из них стараются осуществить мечту всех структурных биоинформатиков — фолдинг (любого) белка in silico на основе данных только о первичной структуре . Идея подходов de novo в том, чтобы заставить полипептидную цепь (то есть «развернутый» белок) принять близкую к нативной конформацию (то есть «свернуться» в нативный фолд) под действием внешних сил (например эмпирического силового поля). Успехи в этой области пока малочисленны, но впечатляют и обещают новые открытия. Подробнее об одном из них можно почитать в статье «Миллисекундный барьер взят!» [62].
Следует заметить, что когда если такая затея станет реальностью, то экспериментальные методы структурной биологии утратят свое нынешнее значение.
Rosetta
«Промежуточным» подходом можно назвать принципы работы программы Rosetta. Она использует конформации олигопептидных фрагментов, которые встречаются в белках с известной структурой, как конструктор, из которого собирается полная структура исследуемого белка. Затем с помощью динамики Монте-Карло производится поиск наиболее оптимальной (низкоэнергетической) конформации. Грубо говоря, проблема фолдинга in silico здесь решается за счет уменьшения количества торсионных углов, которые необходимо оптимизировать, а, соответственно, и степеней свободы полипептидной цепи, которые необходимо учитывать при расчете. Следует отметить, что Rosetta — не единственная программа, использующая такой принцип. Подобным образом работает и сервер I-TASSER, а также другие проекты, решающие проблему de novo моделирования структуры [19].
Волонтерские вычисления и краудсорсинг
Для моделирования структуры и динамики биомолекул необходимы значительные вычислительные ресурсы. Конечно, многие подходы используют для этих целей многопоточные суперкомпьютерные вычисления, однако это связано с большими финансовыми затратами. Сложность и количество задач молекулярного моделирования, вынуждают исследователей придумывать оригинальные способы их решения.
Нередко для решения задач какой-либо узкой области привлекаются люди, которые не имеют никакого отношения к решаемой проблеме — сегодня это называют краудсорсингом. Один из примеров краудсорсинга связан с вышеупомянутой программой Rosetta. Для ее работы используются персональные компьютеры десятков тысяч людей по всему миру, что позволяет моделировать структуру белков с суперкомпьютерной производительностью. Любой человек может стать участником проекта под названием Rosetta@home, предоставив часть ресурсов своего компьютера для выполнения небольшой части расчета оптимальной конформации реального белка, и таким образом внести свой вклад в текущие биохимические/биомедицинские исследования. Такая разновидность краудсорсинга получила название «добровольные вычисления», и сегодня применяется не только в компьютерной биологии, но в самых разнообразных областях, требующих больших расчетов, таких как астрофизика, математика, квантовая механика, изучение климата, искусственный интеллект и др.
Более интересным и оригинальным примером краудсорсинга в компьютерной биологии является программа FoldIt, которую совместными усилиями создали основатели и участники проекта Rosetta@home. Она тоже направлена на поиск нативной конформации белка. Однако ее отличие в том, что для оптимизации геометрии молекулы здесь используются не компьютерные алгоритмы, а логика и интуиция пользователя, потому что FoldIt — это... компьютерная игра. Ее может скачать и установить кто угодно, причем пользователь не обязан иметь каких-либо знаний в химии, физике или биологии, поскольку фактически это «просто» трехмерная головоломка. За изменение структуры начисляются очки, которые напрямую связаны с потенциальной энергией молекулы — так игрок и понимает, что движется в правильном направлении. Самое замечательное, что результаты решения такой головоломки могут стать реальным новым биологическим знанием (подробнее об этом читайте в статьях «Тетрис XXI века» [63] и «Проблема фолдинга белка» [57]).
Молекулярный докинг
Очевидно, для того чтобы отдельные молекулы провзаимодействовали друг с другом, им нужно на какое-то время сблизиться в пространстве и «соприкоснуться», то есть образовать молекулярный комплекс. Это замечание справедливо как для протекания химической реакции (когда образуются/разрушаются химические связи), так и для любого биохимического процесса. Более того, зная строение целого молекулярного комплекса (а не отдельных его частей), гораздо проще понять, как протекает этот самый процесс. Надежнее всего, то есть «напрямую», это удается сделать с использованием методов структурной биологии [6], а в случае действительно больших межмолекулярных систем применяют микроскопию [64] (все чаще — криоэлектронную, за которую в 2017 году вручена Нобелевская премия по химии [30]). Кроме того, «косвенно», но довольно точно, в ряде случаев это можно сделать с использованием данных мутагенетических исследований [25], направленных на установление конкретных элементов молекул, которыми они «соприкасаются» (то есть взаимодействуют). Тем не менее очень часто приходится прибегать к использованию моделирования для предсказания структуры молекулярных комплексов. Одна из самых распространенных методик, которые для этого применяют — молекулярный докинг.
Молекулярная стыковка
«Докинг» переводится с английского как «стыковка» — и в этом буквально заключается суть данного компьютерного эксперимента (рис. 11). Одна молекула фиксируется в пространстве (рецептор), а другая (лиганд) стыкуется к ней в определенной ориентации, и реалистичность результирующего комплекса оценивается с помощью специального алгоритма — оценочной функции. Затем ориентация лиганда и/или место стыковки на рецепторе меняется и процедура повторяется. Программы для молекулярного докинга повторяют этот цикл от нескольких тысяч до нескольких десятков тысяч раз. Таким образом генерируется большой набор вариантов молекулярного комплекса, которые ранжируются по величине оценочной функции; варианты, имеющие низкую оценку, отсеиваются как нереалистичные. Обычно в результате получается несколько десятков или сотен моделей комплекса, имеющих наивысшие оценки. Очень часто задача исследователя сводится к тому, чтобы понять, какая из этих моделей отражает то, что происходит на молекулярном уровне в действительности, и здесь не обойтись без экспериментальных данных об этой (или максимально схожей с ней) молекулярной системе, а также глубоких знаний в области молекулярной биофизики.

Рисунок 11. Молекулярный докинг. Лиганд в различной ориентации и с разных сторон «подсовывают» неподвижному рецептору, а потом оценивают какой из получившихся комплексов «крепче».
рисунок Ольги Пташник
Рецептором в таком эксперименте называют макромолекулу с известной структурой: белок (например фермент), НК (например субъединицу рибосомы) или даже их комплекс. В качестве лиганда обычно выступает низкомолекулярное соединение, для которого экспериментально доказано наличие взаимодействия с этим рецептором или имеются веские основания считать, что такое взаимодействие возможно (подробнее об этом можно узнать из статьи «Драг-дизайн: как в современном мире создаются новые лекарства» [25]). Однако существует и белок—белковый докинг, требующий значительно бóльших вычислительных ресурсов для генерации и оценки реалистичности комплексов, а также времени на обработку результатов, чем белок—лигандный докинг.
Вообще говоря, программы для молекулярного докинга имеют значительные различия как в способах стыковки молекул, так и в алгоритмах оценочной функции. В самом простом случае рецептор и лиганд учитываются программой, как жесткие объемные фигуры (жесткий докинг). Более продвинутые разновидности докинга стараются учесть конформационную гибкость лиганда (полугибкий докинг), некоторых элементов рецептора (гибкий докинг), влияние растворителя и даже проводить оптимизацию результирующих комплексов с использованием метода силовых полей и молекулярной динамики [65]. Но, безусловно, самым важным и тонким звеном любой докинговой программы является оценочная функция, которая в той или иной мере должна коррелировать с изменением свободной энергии при связывании лиганда. Существует огромное количество таких функций, обычно они основаны на учете поверхностной комплементарности, электростатических и вандерваальсовых взаимодействий, гидрофобности [66] и др. Однако, несмотря на многообразие подходов к оценке результатов докинга, пока ни одна оценочная функция не способна однозначно указать на правильную структуру комплекса двух молекул.
О других «сухих» методах
Перечисленные выше методы компьютерной биологии — это далеко не все. Рассказывать о них в одной статье, очевидно, нецелесообразно (интересно, многие ли дочитали до этого абзаца?). Попробуем, однако, перечислить основные области современной биологии, где, не отрываясь от компьютера, получают наибольшее количество реальных научных данных, необходимых для развития знания о живых системах.
В системной биологии [67] используют специфические аналитические подходы к установлению взаимосвязей разных (всех сразу) биохимических процессов (на «Биомолекуле» есть парочка статей, посвященных этой теме [68], [69]).
Геномика, метаболомика, интерактомика и другие «омики» [2] применяют свои хитроумные методики для выявления принципов функционирования живых систем и причин развития различных патологических состояний [70]. «Сухая» нейробиология моделирует на компьютере работу головного мозга, устанавливая важнейшие принципы его работы (об этом «Биомолекула» тоже рассказывала в нескольких публикациях [71–73]).
Анализ структурированных и неструктурированных данных огромных объемов и значительного многообразия (big data), полученных в результате биохимических, медицинских и геномных исследований позволяет устанавливать очень сложные и неочевидные взаимосвязи, например, эпигенетических изменений со старением и патологическими возрастными явлениями [74] (кстати, о том, как такие исследования развивают отечественные ученые, «Биомолекула» рассказывала в статье про одну из лабораторий «Сколтеха» [75]).
С помощью анализа биологических текстов (последовательностей НК и белков) биоинформатика проливает свет на принципы организации и реализации наследственной информации, что необходимо для развития таких прикладных областей, как биотехнология и биомедицина (пример того, как это делают, читайте в статье «Такие разные синонимы» [76]).
Существуют также методы компьютерной обработки естественного языка применительно к биологическим и медицинским текстам [77] для автоматизации поиска, классификации, обобщения и «резюмирования» научных данных, что значительно ускоряет и облегчает работу исследователей.
Наконец, статистический анализ экспериментальных данных — это тоже «сухой» метод (причем, самый старый!), применяемый в молекулярной биологии [78].
Кому и зачем это нужно?
Поскольку «сухие» методы являются неотъемлемой частью современной молекулярной биологии, то не будет преувеличением сказать, что все они нужны исследователям, посвятившим себя этой области. А если без шуток, то эти методы произвели несколько революций в биотехнологии и медицине, не говоря уже о фундаментальной науке. Здесь приведено несколько конкретных примеров, но гораздо больше и подробней об этом можно узнать в других статьях на «Биомолекуле» в разделе «„Сухая“ биология».
Пожалуй, самый яркий пример — это современная концепция создания лекарств [25]. Методы молекулярного моделирования широко применяют для анализа строения конкретных мишеней в организме, их лигандов, выяснения того, как они взаимодействуют друг с другом, а также для моделирования структуры и свойств новых соединений, которые можно применять в терапевтических целях.
Зачастую в медицине и биотехнологии возникают такие ситуации, когда очень нужна молекула с определенными свойствами или биологической активностью, но она пока не открыта. Хотя такая задача очень сложна, методы молекулярного моделирования позволяют рассчитать строение необходимой молекулы, и дело остается лишь за малым — получить ее синтетически или биотехнологически. Так, например, были созданы формолаза, «сшивающая» три молекулы формальдегида в дигидроксиацетон [79]; фермент, осуществляющий элиминацию Кэмпа [80], [81]; фермент KumaMax, расщепляющий глютеновые пептиды [82]; гемагглютинин-связывающие белки, показавшие на животных свою высочайшую эффективность в лечении гриппа [83].
Другой пример связан с «сухим» анализом нуклеотидных последовательностей различных организмов. Так был обнаружен феномен смещения частоты кодонов [76] — одни триплеты чаще используются для кодирования аминокислот, чем другие, и соотношение частых и редких кодонов уникально для довольно узких групп организмов. Более того, показали, что количество т-РНК тем выше, чем «чаще» кодон, аминокислоту которого она несет. Соответственно, если мы попытаемся запихать человеческий ген в кишечную палочку, и будем ждать, что она начнет производить наш белок, скорее всего, этого не произойдет, поскольку бактерия будет постоянно «запинаться при чтении» этого гена — у нее просто не будет хватать т-РНК «нужного сорта». Поэтому в современной биотехнологии и генной инженерии перед внесением генетических модификаций в какой-либо организм принято проверять частоту встречаемости кодонов в его генах и in silico подгонять последовательность под эту частоту. Фактически, вносимый ген является искусственным, но кодирует тот же самый человеческий белок. Все это проделывают, например, при получении фрагментов человеческих антител в бактериях.
Третий пример связан с анализом данных геномного секвенирования человека, а точнее, людей, и при том разных. С каждым годом (да что там — с каждым месяцем!) становится все доступнее «генотипироваться», то есть сравнить свой генотип с генотипами других людей. Зачем это нужно? Дело в том, что имеется значительный и постоянно растущий объем данных о том, как различные заболевания связаны с конкретными мутациями. Таким образом можно выявлять предрасположенность к опасным заболеваниям (по крайней мере, так утверждают компании, предлагающие услуги по генетическому тестированию [84]), например, к диабету или сердечной недостаточности, еще до того, как появятся первые симптомы. А ведь если предупрежден, значит, вооружен — можно принять меры, чтобы патология вообще не развилась в будущем или хотя бы не повлияла на качество жизни. И все это было бы просто невозможно без методов анализа геномной информации, то есть огромного массива нуклеотидных последовательностей.
Как отмечено в предисловии, биология всегда была и всегда будет «мокрой», то есть экспериментальной наукой. Однако «сухие» методы, точнее, возможности, которые они дают, приобретают все бóльшее значение, причем не только для фундаментальной науки, но и для таких прикладных областей, как (био)медицина и (био)технология. Можно с интересом наблюдать за совместным развитием «мокрой» и «сухой» наук... или присоединится к этому увлекательному процессу (подробнее об этом — в статье «Я б в биоинформатики пошел, пусть меня научат!» [4], а также в статьях раздела «Места» на «Биомолекуле»).
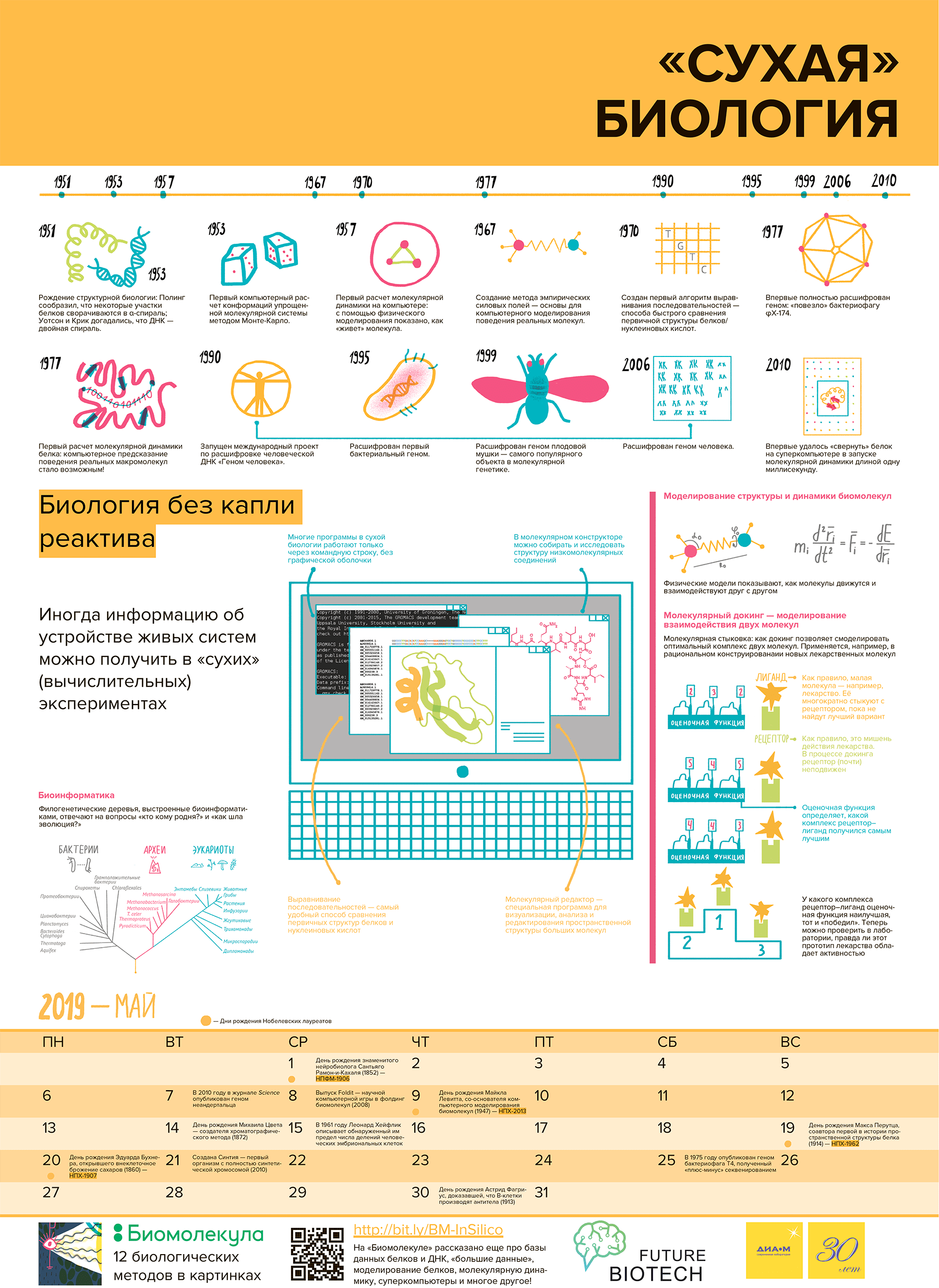
Календарь
На основе статей спецпроекта мы решили сделать календарь «12 методов биологии» на 2019 год. Эта статья представляет май.
Литература
- Вычислительное будущее биологии;
- «Омики» — эпоха большой биологии;
- Жизнь — это компьютер;
- Я б в биоинформатики пошёл, пусть меня научат!;
- Пространственно-временное моделирование в биологии;
- 12 методов в картинках: структурная биология;
- Молекулярная динамика биомолекул. Часть I. История полувековой давности;
- На заре молекулярной графики;
- 12 методов в картинках: секвенирование нуклеиновых кислот;
- От поцелуя до лимфомы один вирус;
- Геном человека: как это было и как это будет;
- Pehr Edman, Erik Högfeldt, Lars Gunnar Sillén, Per-Olof Kinell. (1950). Method for Determination of the Amino Acid Sequence in Peptides.. Acta Chem. Scand.. 4, 283-293;
- Pauling L., Corey R.B., Branson H.R. (1951). The structure of proteins; two hydrogen-bonded helical configurations of the polypeptide chain. Proc. Natl. Acad. Sci. USA. 37, 205–211;
- J. D. WATSON, F. H. C. CRICK. (1953). Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature. 171, 737-738;
- Nicholas Metropolis, S. Ulam. (1949). The Monte Carlo Method. Journal of the American Statistical Association. 44, 335;
- Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, Edward Teller. (1953). Equation of State Calculations by Fast Computing Machines. The Journal of Chemical Physics. 21, 1087-1092;
- McCarthy B.J. and Bolton E.T. (1963). An approach to the measurement of genetic relatedness among organisms. Proc. Natl. Acad. Sci. USA. 50, 156–164;
- P. Edman, G. Begg. (1967). A Protein Sequenator. Eur J Biochem. 1, 80-91;
- Торжество компьютерных методов: предсказание строения белков;
- W.J. Browne, A.C.T. North, D.C. Phillips, Keith Brew, Thomas C. Vanaman, Robert L. Hill. (1969). A possible three-dimensional structure of bovine α-lactalbumin based on that of hen's egg-white lysozyme. Journal of Molecular Biology. 42, 65-86;
- Saul B. Needleman, Christian D. Wunsch. (1970). A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology. 48, 443-453;
- Paulien Hogeweg. (2011). The Roots of Bioinformatics in Theoretical Biology. PLoS Comput Biol. 7, e1002021;
- C. Levinthal, S. J. Wodak, P. Kahn, A. K. Dadivanian. (1975). Hemoglobin interaction in sickle cell fibers. I: Theoretical approaches to the molecular contacts.. Proceedings of the National Academy of Sciences. 72, 1330-1334;
- Irwin D. Kuntz, Jeffrey M. Blaney, Stuart J. Oatley, Robert Langridge, Thomas E. Ferrin. (1982). A geometric approach to macromolecule-ligand interactions. Journal of Molecular Biology. 161, 269-288;
- Драг-дизайн: как в современном мире создаются новые лекарства;
- B. J. Strasser. (2008). GENETICS: GenBank--Natural History in the 21st Century?. Science. 322, 537-538;
- Stevens H. Life out of sequence: a data-driven history of bioinformatics. Chicago: University of Chicago Press, 2013. — 303 p.;
- Edgar E Meyer. (1997). The first years of the Protein Data Bank. Protein Sci.. 6, 1591-1597;
- Helen M. Berman. (2008). The Protein Data Bank: a historical perspective. Acta Cryst Sect A. 64, 88-95;
- Крупные подробности микроскопического мира: Нобелевская премия по химии 2017;
- PDB Current Holdings Breakdown;
- K. Kleppe, E. Ohtsuka, R. Kleppe, I. Molineux, H.G. Khorana. (1971). Studies on polynucleotides. Journal of Molecular Biology. 56, 341-361;
- 12 методов в картинках: полимеразная цепная реакция;
- Rabinow P. Making PCR: a story of biotechnology. Chicago: University of Chicago Press, 1996. — 198 p.;
- 454-секвенирование (высокопроизводительное пиросеквенирование ДНК);
- F. Sanger, A.R. Coulson. (1975). A rapid method for determining sequences in DNA by primed synthesis with DNA polymerase. Journal of Molecular Biology. 94, 441-448;
- Sanger F., Niclein S., Coulson A.R. (1977). DNA sequencing with chain-terminating inhibitors. Proc. Natl. Acad. Sci. USA. 74, 5463–5467;
- C. A. Hutchison. (2007). DNA sequencing: bench to bedside and beyond. Nucleic Acids Research. 35, 6227-6237;
- Stephen F. Altschul, Warren Gish, Webb Miller, Eugene W. Myers, David J. Lipman. (1990). Basic local alignment search tool. Journal of Molecular Biology. 215, 403-410;
- Lesk A.M. Introduction to bioinformatics. Oxford: Oxford University Press, 2002. — 400 p.;
- Сome to the bioinformatics side: Институт биоинформатики в Санкт-Петербурге;
- Sean R Eddy. (2004). What is dynamic programming?. Nat Biotechnol. 22, 909-910;
- T.F. Smith, M.S. Waterman. (1981). Identification of common molecular subsequences. Journal of Molecular Biology. 147, 195-197;
- Как прочитать эволюцию по генам?;
- Карл Вёзе (1928–2012);
- In vivo — in vitro — in silico;
- «Виртуальная» Нобелевская премия по химии (2013);
- Роль слабых взаимодействий в биополимерах;
- Молекулярная поверхность: что в облике тебе моём?;
- Виртуальные тропы реальных лекарств;
- Рождение виртуальной клеточной биологии;
- У истоков генетического кода: родственные души;
- Компьютерные игры в молекулярную биофизику биологических мембран;
- Калиевый канал in silico;
- Juan R. Perilla, Klaus Schulten. (2017). Physical properties of the HIV-1 capsid from all-atom molecular dynamics simulations. Nat Comms. 8, 15959;
- Фолдинг «воочию»;
- Проблема фолдинга белка;
- Одна последовательность — одна структура: был ли Анфинсен неправ?;
- Непохожие «гомологичные» белки;
- Недоупорядоченные белки;
- За пределами порядка;
- Миллисекундный барьер взят!;
- Тетрис XXI века;
- 12 методов в картинках: микроскопия;
- DOCK 6. The Official UCSF DOCK Web-site;
- Физическая водобоязнь;
- Гельфанд М. (2013). Системная биология. «Постнаука»;
- Биоинформатика: большие БД против «большого Р»;
- ACSN — глобальный атлас сигнальных путей. От молекулярной географии рака к новым информационным технологиям в биологии;
- По карте интерактома можно найти неожиданные связи между болезнями;
- Хаос в мозге;
- Blue brain project: связи и хаос;
- Blue Brain Project: как все связано?;
- Старение и долголетие: эпигеном раскрывает тайны;
- Исследовательская группа Филиппа Хайтовича, или Как биологи работают с большими массивами данных;
- Такие разные синонимы;
- Что хотел сказать автор?;
- Статистика: наглядное пособие;
- Justin B. Siegel, Amanda Lee Smith, Sean Poust, Adam J. Wargacki, Arren Bar-Even, et. al.. (2015). Computational protein design enables a novel one-carbon assimilation pathway. Proc Natl Acad Sci USA. 201500545;
- Дизайнерские ферменты на службе общества;
- Daniela Röthlisberger, Olga Khersonsky, Andrew M. Wollacott, Lin Jiang, Jason DeChancie, et. al.. (2008). Kemp elimination catalysts by computational enzyme design. Nature. 453, 190-195;
- Sydney R. Gordon, Elizabeth J. Stanley, Sarah Wolf, Angus Toland, Sean J. Wu, et. al.. (2012). Computational Design of an α-Gliadin Peptidase. J. Am. Chem. Soc.. 134, 20513-20520;
- Merika Treants Koday, Jorgen Nelson, Aaron Chevalier, Michael Koday, Hannah Kalinoski, et. al.. (2016). A Computationally Designed Hemagglutinin Stem-Binding Protein Provides In Vivo Protection from Influenza Independent of a Host Immune Response. PLoS Pathog. 12, e1005409;
- Константинов А. (2016). Просто наплевать. «Кот Шрёдингера».