В поисках новых лекарств: математическое моделирование поведения живой клетки
08 ноября 2018
В поисках новых лекарств: математическое моделирование поведения живой клетки
- 2232
- 0
- 10
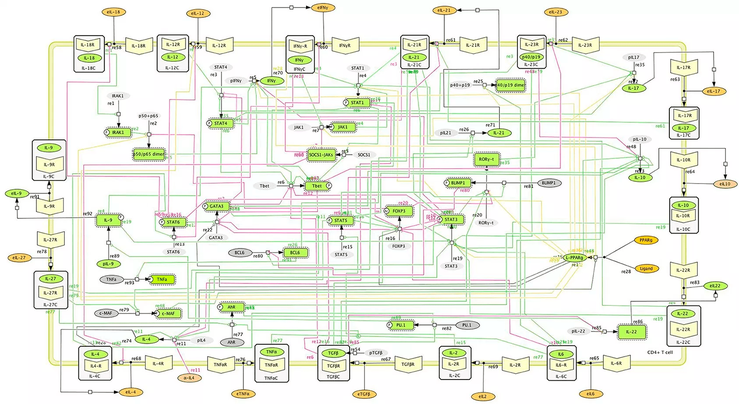
При взгляде на эту упрощенную схему сигнальной сети живой клетки очень трудно разобраться, как клетка работает. А предсказать поведение такой системы после воздействия на любой узел оказывается и вовсе нетривиальной задачей. Рисунок в полном размере можно посмотреть здесь.
-
Автор
-
Редакторы
Темы
Статья на конкурс «био/мол/текст»: Какие механизмы лежат в основе развития того или иного заболевания? И как найти необходимое лекарственное средство для того, чтобы справиться с болезнью? Ответы на эти вопросы может дать системная биология — область знаний, рассматривающая клетку как сложную систему взаимодействующих элементов. Ее основным методом является математическое моделирование свойств динамических биологических систем. В этой статье будут разобраны принципы такого моделирования.
Конкурс «био/мол/текст»-2018
Эта работа опубликована в номинации «Биофармацевтика» конкурса «био/мол/текст»-2018.

Партнер номинации — медицинская компания «Инвитро».

Генеральный спонсор конкурса — компания «Диаэм»: крупнейший поставщик оборудования, реагентов и расходных материалов для биологических исследований и производств.

Спонсором приза зрительских симпатий выступил медико-генетический центр Genotek.

«Книжный» спонсор конкурса — «Альпина нон-фикшн»
Одной из причин развития того или иного патологического состояния является дисрегуляция каких-либо сигнальных путей в клетке. Логическое моделирование играет особую роль при построении моделей клеточного сигналинга. Основная идея этого подхода заключается в создании модели с использованием логических операторов (AND, OR, NOT), которая будет предсказывать поведение клетки при воздействии на какие-либо компоненты сигнальной сети, например, при использовании потенциального лекарственного препарата.
В данной статье рассмотрены принципы построения таких логических моделей на примере гипотетического сигнального пути, а также представлены результаты моделирования реальных сигнальных сетей в клетках рака печени и рака простаты. Логическое моделирование клеточного сигналинга наглядно демонстрирует отличия в сигнальных путях между здоровой и злокачественной клеткой. В перспективе это может облегчить исследователям задачу по поиску новых мишеней для таргетной терапии рака, избавив их от рутинной работы в лабораториях при скрининге десятков потенциальных молекул-кандидатов. Кроме того, логическое моделирование может изменить наше представление о медицине, а именно, сделать возможным индивидуальный подход при установлении причин заболевания, прогнозировании его течения и подборе лекарственных препаратов.
Как исследователи открывают новые лекарства?
Поиск новых лекарственных препаратов является весьма трудоемкой задачей. И задача эта становится подчас непосильной, когда неизвестны причины, которые привели к развитию заболевания. Существуют два принципиально разных подхода, которые применяются для поиска новых препаратов.
Первый заключается в тестировании потенциального лекарства в биологической системе — культуре клеток, изолированных тканях и органах или животных, чтобы увидеть, оказывает ли исследуемое вещество желаемый эффект (phenotypic screening). Однако при таком подходе фактический механизм действия препарата остается неизвестным, подчас даже в течение многих лет после открытия лекарства [2].
Другой подход заключается в выборе мишени в клетке, на которую мы хотим целенаправленно воздействовать с дальнейшим «перебором» молекул-кандидатов на роль нового лекарственного препарата, который лучше всех справится с поставленной задачей (target-based screening) [2].
Хотя у каждого метода есть как свои достоинства, так и недостатки, их общей чертой является трудоемкость. Существуют методики, позволяющие повысить производительность «поиска» новых лекарств (CRISPR-Cas [3–5], shRNA [6–8], микрофлюидика [9], [10]). Однако найденные потенциальные кандидаты, дающие многообещающие результаты, очень часто не обладают желательным терапевтическим эффектом в клинических испытаниях.
Ключом к успеху может стать системный подход в биологии. Исследователи часто рассматривают клетку как своеобразный «черный ящик»: ей дают интересующее вещество и затем наблюдают за ответной реакцией. Конечно, ученые пытаются «приоткрыть завесу тайны» и понять, что же происходит внутри клетки, например, какие гены / белки / белковые комплексы стоят за тем или иным заболеванием. И человечество накопило уже огромный фактический материал и про генетические нарушения, и про белковые взаимодействия в различных клетках/тканях/органах в норме и патологии. Иногда исследователям везет, и они могут «поймать за руку» виновника, как, например, в случае моногенных заболеваний . Но так бывает далеко не всегда. В связи с этим возникает вопрос: стали ли мы ближе к пониманию истинных причин развития того или иного заболевания при накоплении большого количества данных? Или, проще говоря, видим ли мы лес за деревьями?
Эти заболевания определяются одним геном и наследуются согласно законам Менделя.
Клетка как система
Системный подход подразумевает рассмотрение живой клетки как сложной системы взаимодействующих элементов. Отличительной чертой этой системы является ее способность воспринимать различные стимулы окружающей среды и в ответ на эти стимулы изменять свое поведение и фенотип , осуществляя тонкую подстройку к изменившимся условиям среды.
Совокупность биологических свойств и признаков организма, сложившаяся в процессе его индивидуального развития.
В этой системе можно выделить несколько уровней организации (рис. 1). Первый уровень представляет собой ДНК — носитель генетической информации. В ДНК находится информация о последовательности белков, а также многочисленные «инструкции» о том, как реализовывать эту информацию, — регуляторные последовательности. Второй уровень — это мРНК (матричные РНК), которые синтезируются на базе ДНК и, в свою очередь, являются матрицами для синтеза белков . Третий уровень представляет собой белки — «клеточные машины». Они выполняют огромное количество функций — в частности, являются биологическими катализаторами многочисленных клеточных реакций, выполняют строительные и моторные функции, отвечают за передачу сигналов о действии различных факторов среды на клетку и т.д. Таким образом, можно применять системный подход к клетке на разных уровнях: можно исследовать ее геном (различные мутации, вариации в последовательностях и пр.), транскриптом, протеом . Важно помнить то, что эти уровни тесно связаны между собой, и то, что различные факторы среды, будь они химической природы (гормоны, факторы роста, цитокины, аутокринные факторы и т.д.) или физической природы (температура, давление, электрический импульс) оказывают влияние на клетку на всех этих уровнях. Принято говорить, что они создают особый «контекст» для клетки (рис. 1).
Кроме мРНК в клетке синтезируется большое количество РНК, которые не кодируют белки — некодирующие РНК (нкРНК), которые, как правило, выполняют регуляторные функции [8].
«Омы» (геном, трансриптом, протеом и т.д.) в биологии обозначают совокупность каких-либо однородных объектов. В частности, геном — совокупность всех генов, транскриптом — совокупность всех молекул РНК, которые синтезируются в клетке/ткани/организме, протеом — совокупность всех синтезированных белков в клетке/ткани/организме. Причем в современной биологии появились самостоятельные направления — «омики», которые изучают эти совокупности: геномика, трансриптомика, протеомика и т.д (или «омиксные» технологии) [11].
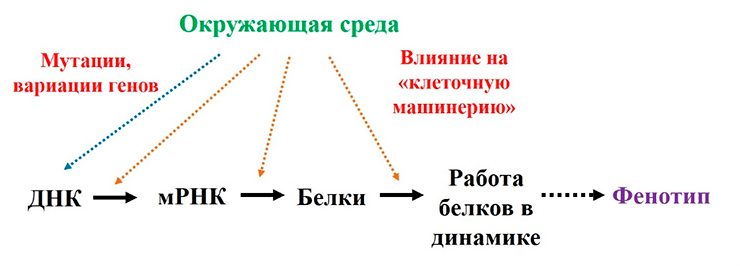
Рисунок 1. Уровни организации клетки как системы. Факторы окружающей среды оказывают влияние на всех уровнях, создавая определенный «контекст».
[21], рисунок с изменениями
Можно привести изящный пример, который иллюстрирует необходимость применения системного подхода и принятия во внимание «клеточного контекста» при исследовании действия лекарственных препаратов. Известно, что специфическая мутация в гене BRAF (V600E) в клетках меланомы приводит к усилению деления раковых клеток. Вещество вемурафениб (vemurafenib, V600E mutated BRAF inhibition), применяемое при лечении меланомы, точечно действует на мутантный белок и препятствует росту опухоли. Однако пациенты с раком толстого кишечника с точно такой же мутацией не отвечают на лечение вемурафенибом. Разница в этих двух ответах на лекарство как раз и заключается в тех стимулах, которые получают клетки меланомы и клетки рака толстого кишечника. В данном случае в клетках рака толстого кишечника активируется сигнальный путь через рецептор EGFR, что в конечном счете и приводит к усилению клеточного деления даже в присутствии вемурафениба [12]. Этот пример наглядно показывает, как важно понимать процессы, протекающие внутри «черного ящика», и ту роль, которую играют внешние стимулы.
Рассмотрением клетки как системы занимается область знаний под названием системная биология. Эта активно развивающаяся междисциплинарная наука анализирует сложные биологические системы с учетом их многокомпонентности, наличия прямых и обратных связей, разнородности и большого количества экспериментальных данных. Основной задачей системной биологии является моделирование свойств биологической системы на различных уровнях ее организации, начиная от регуляции экспрессии генов, клеточного метаболизма и заканчивая клеточной динамикой и взаимодействиями в клеточной популяции. На рисунке 2 представлена схема, иллюстрирующая, какое место занимает системная биология среди наук, использующих математический инструментарий для исследования живых систем, так называемых «сухих» методов биологии [13], [14].
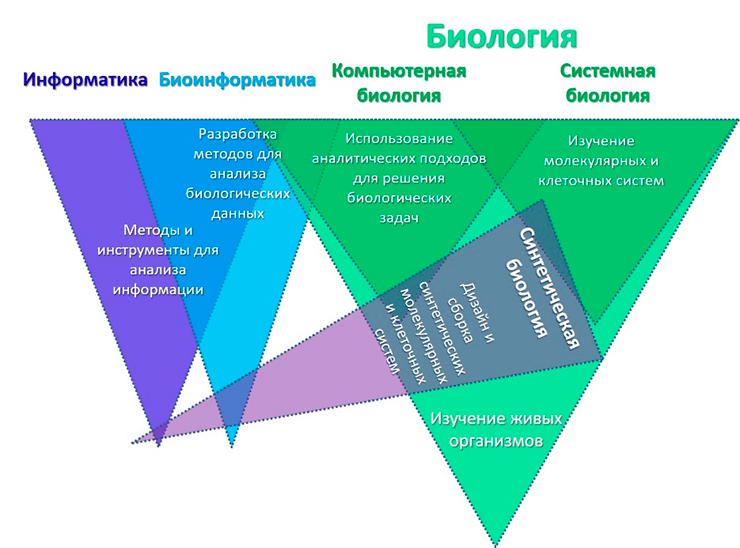
Рисунок 2. Пересечение различных дисциплин, использующих математический инструментарий для изучения живых систем. Биоинформатика [15] занимается разработкой новых методов анализа биологических данных (последовательности, пространственные структуры молекул, молекулярные взаимодействия — докинг) и новых баз данных для хранения этой информации. Компьютерная биология использует методы биоинформатики и другие аналитические подходы для решения определенных задач (например, создание новых лекарств [16], [17] путем определения макромолекул-мишеней, поиск низкомолекулярных компонентов). Системная биология занимается моделированием свойств динамических биологических систем на молекулярном и клеточном уровнях. Синтетическая биология относится к инженерным наукам и занимается дизайном и построением синтетических биологических систем [18].
[33], рисунок с изменениями
Передача информации в клетке в норме и патологии
Какие же механизмы лежат в основе развития тех или иных патологических состояний в клетке, например, трансформации нормальной клетки в злокачественную? На эту проблему можно посмотреть с разных точек зрения. Например, можно исследовать геном в поисках различных генетических нарушений, которые могут быть ассоциированы с развитием того или иного заболевания. В примере с меланомой кандидатом на роль главного «злодея» стал ген BRAF, несущий мутацию. Есть и другие примеры. На рисунке 3 представлена схема, иллюстрирующая генетические нарушения (каждый столбик представляет собой десятки разнообразных мутаций), выявленные при анализе рака поджелудочной железы у 24 пациентов. Из схемы следует, что сотни разнообразных генетических нарушений, которые варьируют от пациента к пациенту, приводят к одному и тому же результату — злокачественному перерождению клеток поджелудочной железы [19]. Подобная картина характерна и для многих других видов рака, например, рака молочной железы, толстого кишечника, опухоли мозга и т.д. [20].
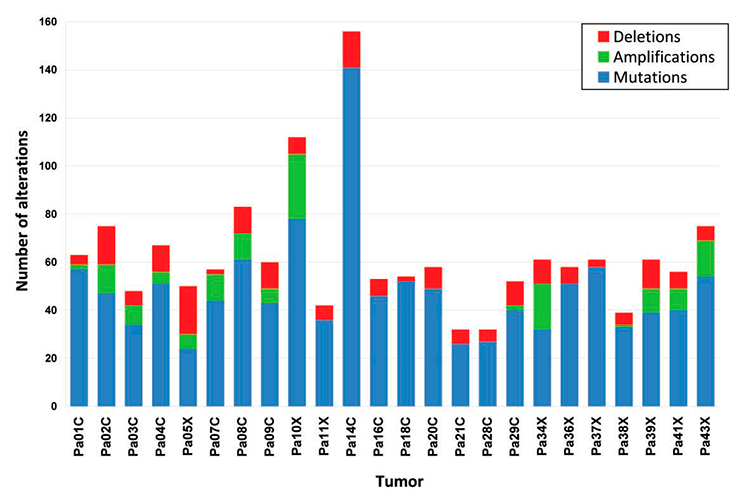
Рисунок 3. Генетические нарушения, выявленные методами секвенирования и количественного анализа у 24 пациентов с раком поджелудочной железы. Обозначения: делеции — красным цветом; амплификации — зеленым; мутации — синим.
Однако если посмотреть на эту проблему с другой стороны, то разнообразные нарушения на генном уровне «затрагивают» ограниченный набор ключевых сигнальных путей на уровне белков.
Для того чтобы понять, что такое клеточный сигналинг, рассмотрим в качестве примера действие на клетку агента химической природы — например, гормона. Передача информации о приходящем стимуле внутрь клетки — многоступенчатый процесс. Молекула гормона связывается со специфическим белком-рецептором, находящимся на поверхности клетки. При связывании с молекулой гормона рецептор переходит в активированное состояние, «привлекает» других участников сигнального пути и передает информацию далее по цепочке. С механистической точки зрения сигнальный путь представляет собой каскад биохимических реакций, в ходе которых вышестоящий и нижестоящий участники — белковые молекулы — находятся в отношениях «фермент—субстрат»: фермент взаимодействует со своим субстратом и модифицирует его (часто путем фосфорилирования/дефосфорилирования ). Модифицированный субстрат далее передает информацию ниже по цепочке.
Процесс переноса остатка фосфорной кислоты от фосфорилирующего агента-донора к субстрату.
Дисрегуляция каких-либо сигнальных путей может стать причиной развития патологического состояния, например, злокачественной трансформации клеток [21]. В случае рака поджелудочной железы можно обрисовать круг тех метаболических путей, которые наиболее часто нарушаются при злокачественном перерождении клетки (рис. 4). И хотя ситуация выглядит лучше, если при изучении клеточного сигналинга «спуститься» с уровня ДНК на уровень белков (рис. 1), за каждым названием сигнального пути (Jnk signaling, TGFβ signaling и т.д.; рис. 3) стоит большое количество белков-участников. Более того, сигнальные пути часто пересекаются, взаимодействуют друг с другом (crosstalk), дополняют или дублируют друг друга. Поэтому в биологии принято говорить о сигнальных сетях.
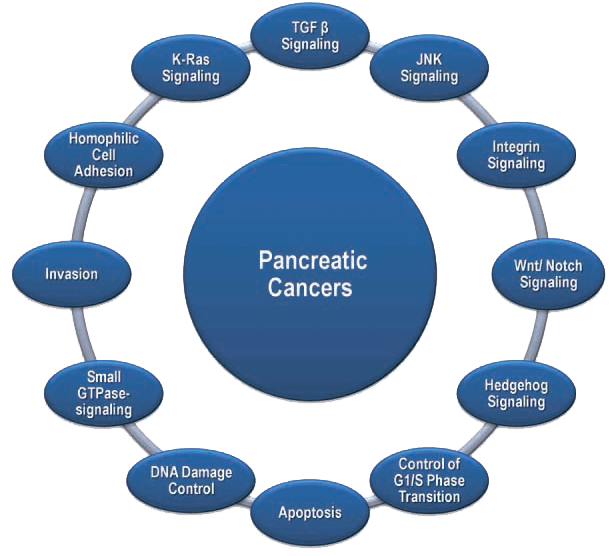
Рисунок 4. Сигнальные пути и клеточные процессы, нарушение которых характерно для разных типов рака поджелудочной железы
В качестве заглавной иллюстрации к этой статье изображена упрощенная схема сигнальной сети клетки иммунной системы Т-лимфоцита CD4+ [1]. Несмотря на то, что на ней показаны только ключевые участники сети (полная картина выглядит куда более сложно), эту и подобные ей схемы крайне трудно интерпретировать. Большой объем информации не только не вносит больше понимания в принципы работы сигнальных сетей, но и, наоборот, подчас не позволяет уловить логику процесса. Также используя такой подход представления информации, исследователи не могут предсказать поведение клетки в ответ на действие того или иного стимула или комбинации стимулов. Таким образом, необходимо применение принципиально новых подходов для решения поставленных задач.
Принципы логического моделирования клетки
На помощь приходит математическое моделирование поведения клетки. В зависимости от объема «первичной информации» (prior knowledge) о системе, которой мы располагаем, все компьютерные методы моделирования условно можно представить в виде спектра (рис. 5) [16], [17], [22], [23]. Для моделирования сигнальных сетей клетки может использоваться различный математический инструментарий, среди которого логическое моделирование занимает особое место. Этот подход применяется преимущественно при моделировании клеточного сигналинга и процессов генной регуляции, хотя существуют логические модели и других биологических процессов (гематопоэз [24], апоптоз). По сравнению с другими методами математического моделирования, логические модели лучше подходят для «описания» достаточно больших сигнальных сетей, в случае, когда исследователи не обладают всей полнотой информации о системе. В таком случае схематическое представление может облегчить понимание сути процессов и улучшить интерпретируемость полученных результатов.
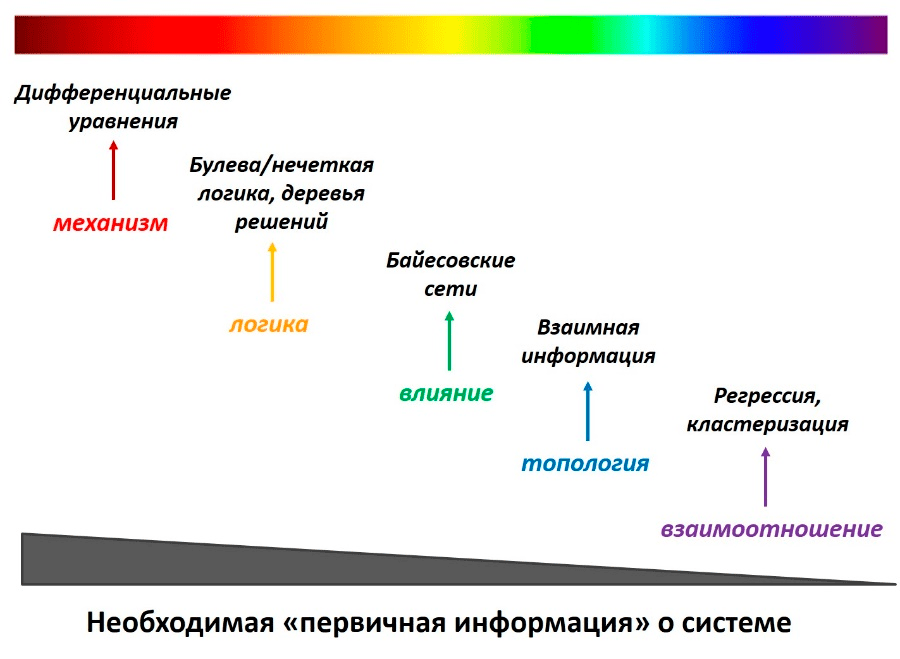
Рисунок 5. Спектр компьютерных методов моделирования. В зависимости от объема «первичной информации» о системе методы моделирования можно представить в виде спектра, причем с уменьшением этой информации растет уровень абстракции модели. Например, на одном крае спектра находится дифференциальное исчисление, которое используют в случае наличия «механистической информации», то есть когда известны точные механизмы взаимодействия участников сигнальной сети и можно оценить константы скоростей реакций. Таким образом, написав дифференциальные уравнения для десятков компонентов, можно предсказать их взаимодействие в динамике. На другом крае спектра находятся такие методы, как кластеризация и регрессионный анализ, которые позволяют оценить влияние одной или нескольких независимых переменных на зависимую переменную или разбить множество объектов на классы по тем или иным признакам соответственно.
«Первичную информацию» о клеточном сигналинге можно почерпнуть из литературных данных, а также из специализированных баз данных. Можно выделить две группы таких баз данных: «интерактомы» (interactomes) [25], или, как их по-другому называют, PINs (protein interaction networks) и PSNs (protein signaling networks). PIN представляет собой граф, в узлах которого находятся белковые молекулы-участники сигнального каскада (клеточные рецепторы, киназы, фосфатазы и др.), а стрелки показывают взаимодействия между ними. PSN также является графом, но в отличие от PIN он содержит информацию о характере взаимодействия белковых молекул (активация — «+» — или ингибирование — «−») (рис. 6) [22].
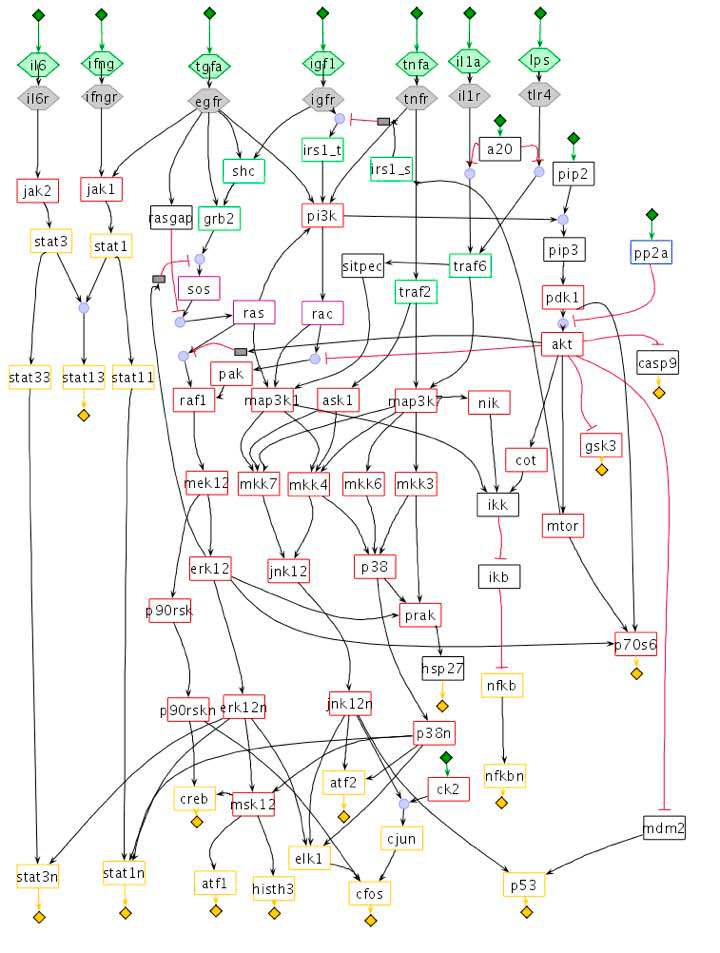
Рисунок 6. Пример участка сигнальной сети типа PIN, иллюстрирующей ответ клетки на действия цитокинов и различных факторов роста. Сигнальная сеть содержит ключевые рецепторы и суммарно насчитывает 82 узла и 116 дуг.
Основная идея логического моделирования заключается в том, чтобы при использовании «первичной информации» создать модель, описывающую различные компоненты системы и их взаимодействия, а также способную предсказывать поведение клетки в результате влияния (активация/ингибирование) на какие-либо компоненты этой системы. Для этого на основе «первичной информации» строится так называемая топологическая карта типа PSN. Затем с помощью специальных алгоритмов переходят к логической модели, где используют операторы AND, OR, NOT. Операторы OR и AND соответствуют состоянию активации нижестоящего участника сигнального каскада при действии хотя бы одного или одновременно двух вышестоящих «исполнителей» соответственно. Оператор NOT, в свою очередь, соответствует процессу ингибирования нижестоящего участника сигнальной сети вышестоящим игроком (рис. 7).
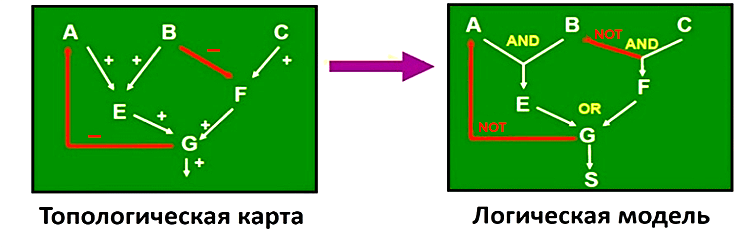
Рисунок 7. Переход от качественной модели сигнальной сети к логической модели. В узлах находятся компоненты сети (киназы, фосфатазы и др.). Стрелки показывают направленность действия: «+» — активация; «−» — ингибирование.
[21], рисунок с изменениями
На следующем этапе полученную логическую модель «обучают» с использованием экспериментальных данных и оптимизируют. Наконец, построенную модель можно применить для «предсказания» поведения системы.
Создание, сборка и анализ логической модели клеточного сигналинга
Рассмотрим вначале процесс построения логической модели клеточного сигналинга на примере гипотетической сигнальной сети (toy pathway), включающей всего 18 участников (настоящие сигнальные сети включают несколько десятков игроков). Участники пути в данном примере представляют собой внутриклеточные белки, которые активируются при стимуляции рецептора к эпидермальному фактору роста (epidermal growth factor receptor, EGFR) или рецептора фактора некроза опухоли (tumor necrosis factor receptor, TNFR) (рис. 8а) [22]. «Первичную информацию» об этой сигнальной сети для построения карты типа PSN мы предположительно могли взять из данных литературы и/или различных баз данных.
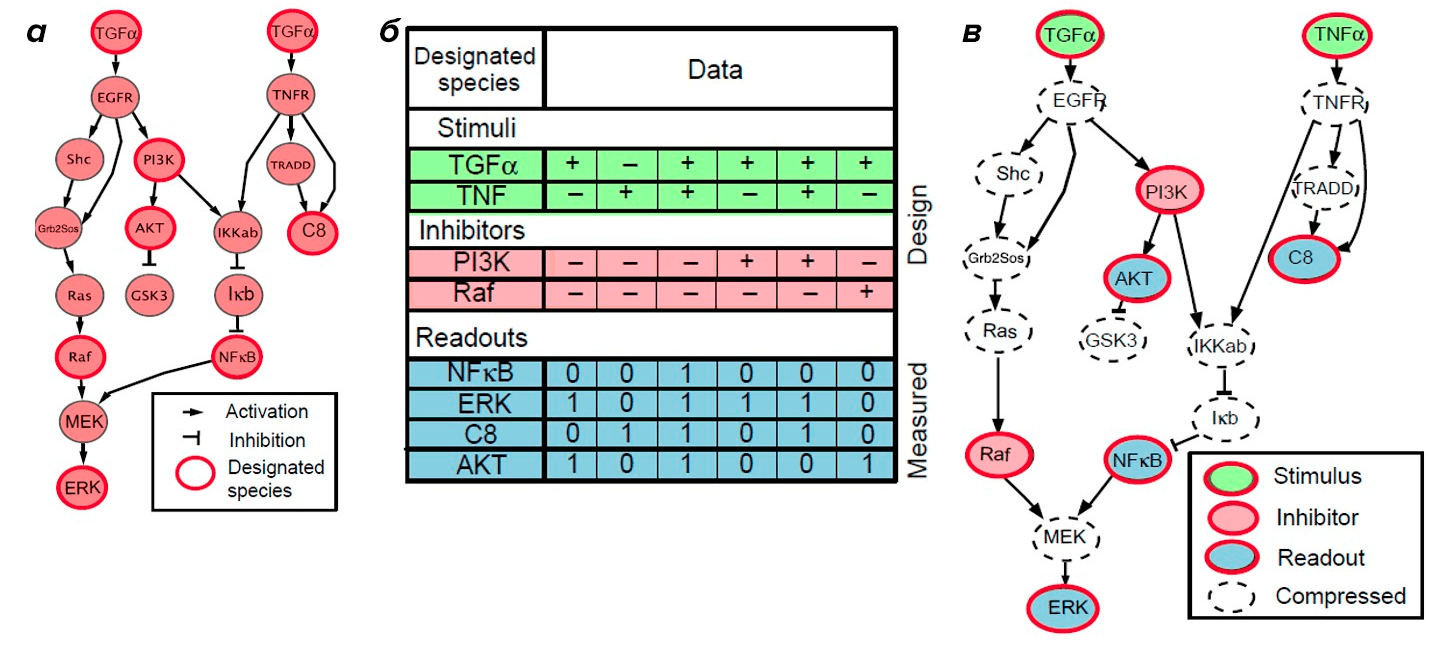
Рисунок 8. Сборка гипотетической сигнальной модели. а — PSN, или топологическая карта, представляющая собой ориентированный граф, то есть совокупность множества вершин и множества связей между вершинами (ребра), которые имеют направление. б — Схема гипотетического эксперимента по «обучению» модели: зеленым цветом показаны лиганды; красным цветом — белки-мишени для ингибиторов; а синим — белки, у которых был измерен уровень фосфорилирования. Присутствие/отсутствие лиганда или ингибитора отмечено знаками «+» и «−» соответственно. Значения 0/1 показывают результат воздействия на участника сигнальной сети при действии определенной комбинации лигандов и ингибиторов. в — Компрессия графа: пунктиром отмечены узлы, которые были удалены.
[22], рисунок с изменениями
Получение экспериментальных данных
Следующий этап моделирования предполагает проведение серии экспериментов для получения «сырых данных» для «обучения модели» (model training). Эти эксперименты заключаются в использовании химических агентов в различных комбинациях для стимуляции/ингибирования одних участников сигнальной сети с последующим «считыванием» (readout) информации о состоянии других участников. В данном случае таким сигналом о состоянии системы после воздействия служит уровень фосфорилирования белков-участников относительно нулевой точки во времени, соответствующей времени до воздействия. Сложность здесь заключается в том, что для моделирования реальной сигнальной сети необходимо собрать информацию об изменении уровня фосфорилирования нескольких десятков белков. Эту задачу можно решить с помощью высокопроизводительного иммунологического анализа xMAP Technology (x-Multi-Analyte Profiling Technology, где х обозначает исследуемый биомаркер). Суть xMAP Technology состоит в использовании наборов (сетов, sets) микроскопических шариков, которые различаются по своим спектральным свойствам (рис. 9а и 9б). Далее к каждому набору таких микросфер химически «пришивают» строго определенные антитела, которые способны «узнавать» свою мишень — антиген. После этого смесь разных наборов микросфер добавляют к пробе (рис. 9в и 9г). Далее специальный анализатор при использовании двух различных источников возбуждающего света вызывает эмиссию флуоресценции и регистрирует тип набора и, при наличии мишени, комплекс антиген—антитело. Таким образом за один эксперимент можно определить порядка 500 мишеней [26]! В данном случае предложенным способом можно определять уровень фосфорилирования белков-участников сигнальной сети.
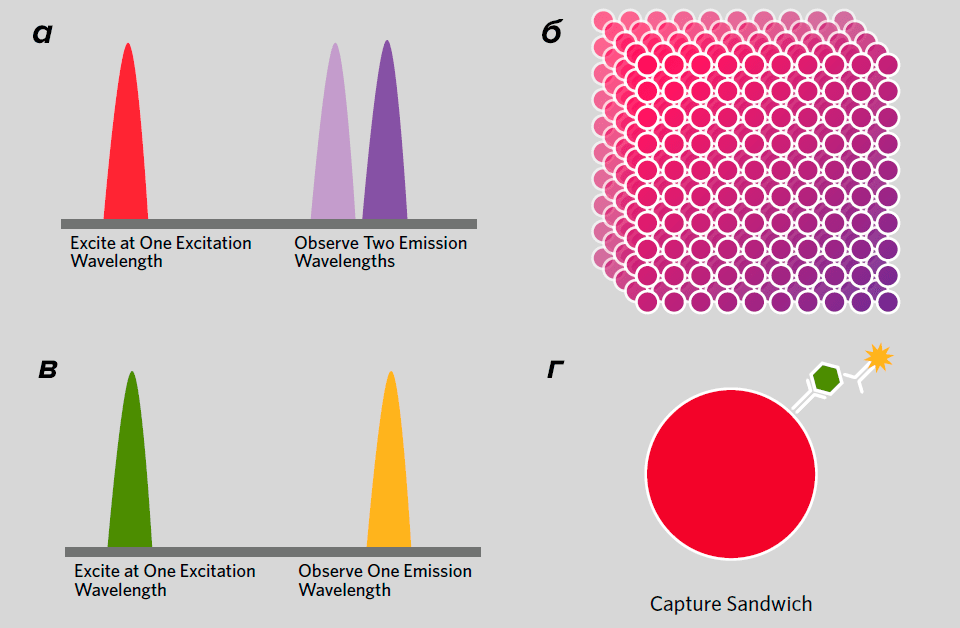
Рисунок 9. xMAP Technology. а — Микросферы включают в себя три красителя, так что при их возбуждении светом определенной длины волны можно регистрировать флуоресценцию на трех длинах волн. б — Различное соотношение трех красителей позволяет получить 500 наборов микросфер, которые различаются спектрами флуоресценции . в — Возбуждение микросфер светом другой длины волны позволяет регистрировать комплекс антиген—антитело. г — Схематическое изображение комплекса антиген—антитело: красным цветом показана микросфера, зеленым цветом — мишень (белок); белым цветом — «сшитое» с микросферой антитело и детекторное антитело, содержащее флуоресцентную метку (желтую).
Флуоресценция — это излучение света веществом, атомы которого получили избыточное количество энергии в результате поглощения другого, как правило, более коротковолнового излучения. Спектр флуоресценции — это зависимость интенсивности флуоресценции от длины волны детекции; в простейшем случае зависимость имеет вид асимметричной кривой с одним максимумом [27].
[26], рисунок с изменениями
Далее полученный сигнал нормируют таким образом, чтобы конечное значение находилось на отрезке [0; 1] (рис. 10). Для этого исследователи разработали специальное программное обеспечение DataRail software [22]. Причем значения, приближающиеся к 1, соответствуют активации, а к 0 — дезактивации участника сигнальной сети.

Рисунок 10. Нормализация экспериментальных значений. Sk,l,t — Уровень сигнала при измерении в k условиях в эксперименте l в точке времени t. Sl,N — Уровень «шума», ниже которого сигнал нельзя идентифицировать. Sl,SAT — Максимально допустимый уровень «насыщения» сигнала. Таким образом, были рассмотрены только те значения Sk,l,t, которые входят в интервал (Sl,N, Sl,SAT). Далее с помощью метода нелинейной нормализации получали конечные значения, которые принадлежали отрезку [0; 1].
[22], рисунок с изменениями
В рассматриваемом нами примере гипотетической сигнальной сети использовали только две крайние точки {0; 1}, тогда как при проведении реальных экспериментов значения лежат на отрезке [0; 1]. Как видно из рисунка 7б, стимуляции гипотетически подвергались рецепторы к EGF и TNF. С помощью молекул-ингибиторов информационные сигналы «прерывали» на уровне PI3K и Raf. Уровень фосфорилирования измеряли у молекул NFkB, ERK, C8 и AKT.
Построение первичной логической модели и ее оптимизация
На следующем этапе моделирования на основе топологической карты строили первичную логическую модель. Для этой цели в лаборатории Хулио Саез-Родригеса (Julio Saez-Rodriguez) разработали специальное программное обеспечение (CellNetOptimazer, CNO) для «сжатия» (компрессии, compression) PSN, которое заключается в удалении из схемы тех узлов, которые не задействованы в эксперименте (рис. 7в) [22]. Далее происходит собственно построение первичной логической модели, включающей операторы AND, OR и NOT [28]. Однако существует множество моделей, которые с той или иной точностью «описывают» сигнальную сеть. Их представляют в виде суперпозиции, в которой реализованы все варианты взаимодействия участников сигнальной сети. Это и есть первичная логическая модель (рис. 11а).
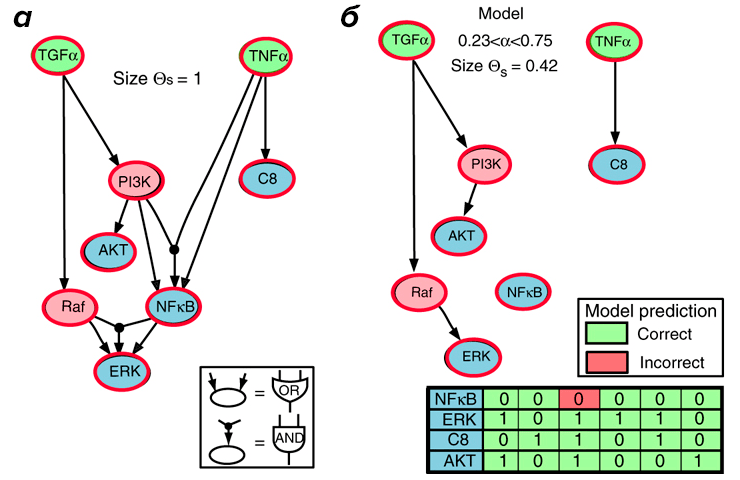
Рисунок 11. Оптимизация логической модели. а — Первичная логическая модель. б — Оптимизированная логическая модель. Таблица показывает соответствие между теоретическими значениями и экспериментальными данными (красным цветом отмечено несоответствие).
[22], рисунок с изменениями
Следующим шагом является «обучение» и оптимизация модели с использованием экспериментальных данных. Для этого исследователи используют целевую функцию Θ(P), включающую два слагаемых [21], [22]:
Θ(P) = Θf(P) + α×Θs(P)
Первое слагаемое Θf(P) (f — от англ. fit) показывает, насколько реальные данные, полученные в ходе эксперимента, соотносятся с модельными значениями, причем чем сильнее расхождение между теоретически предсказанными значениями и «сырыми данными», тем больше слагаемое Θf. Второе слагаемое Θs(P) (s — от англ. size) отвечает за размер модели: чем больше дуг соединяет узлы, тем больше Θs(P). Коэффициент α (penalty) учитывает веса двух слагаемых и подбирается «вручную». Оптимизация заключается в том, чтобы найти среди множества различных вариантов модель наименьшего размера, которая будет наиболее точно «описывать» экспериментальные данные. На языке математики это означает, что нужно найти минимум целевой функции Θ(P) [21], [22].
Для поиска лучшей логической модели используют генетический алгоритм, который включает следующие шаги (рис. 12) [21], [22]:
- Старт: создание популяции моделей.
- Соответствие: определение значения целевой функции для каждой модели.
- Создание новой популяции моделей: новая популяция моделей создается на базе старой в процессе отбора моделей с наименьшим значением целевой функции (селекция), внесения случайных изменений (мутаций) и генерирования новых моделей путем заимствования каких-либо участков у родительских моделей (кроссинговер).
- Замена: новая популяция моделей заменяет старую, причем пять лучших моделей из старой популяции переходят в новое поколение без изменений.
- Цикл: переход к п. 2.
- Стоп: алгоритм будет «работать» до тех пор, пока значение целевой функции перестанет значимо изменяться.
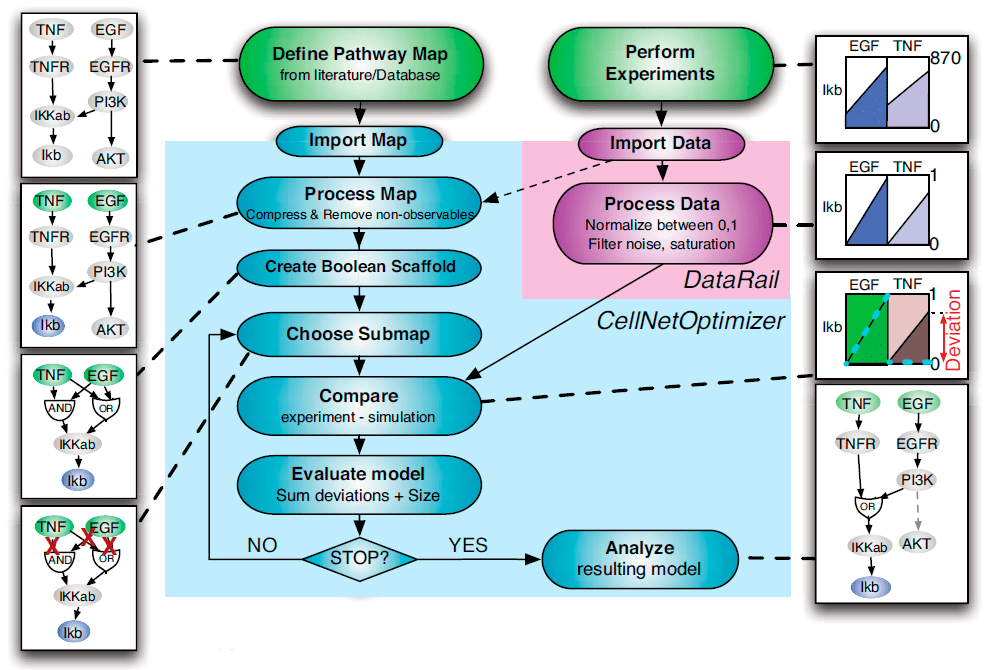
Рисунок 12. Основные этапы построения логической модели клеточного сигналинга
[21], рисунок с изменениями
После нахождения лучшей логической модели приступают к самому интересному — анализу полученных результатов и предсказанию поведения клетки в ответ на добавление каких-либо стимуляторов, ингибиторов, лекарственных веществ и т.д.
Моделирование сигнальной сети различных клеточных линий гепатоцитов
Результаты логического моделирования сигнальной сети клетки выглядят поистине впечатляющими. Рассмотрим в качестве первого примера логическое моделирование сигнальной сети клеток печени — гепатоцитов. Модель наглядно демонстрирует различия в клеточном сигналинге между гепатоцитами здорового донора (первичные клетки) и клетками рака печени (HCC cells) (рис. 13) [21], [29]. То есть с помощью логического моделирования можно вычислить «слабое звено», которое привело к злокачественной трансформации, и целенаправленно на него воздействовать.
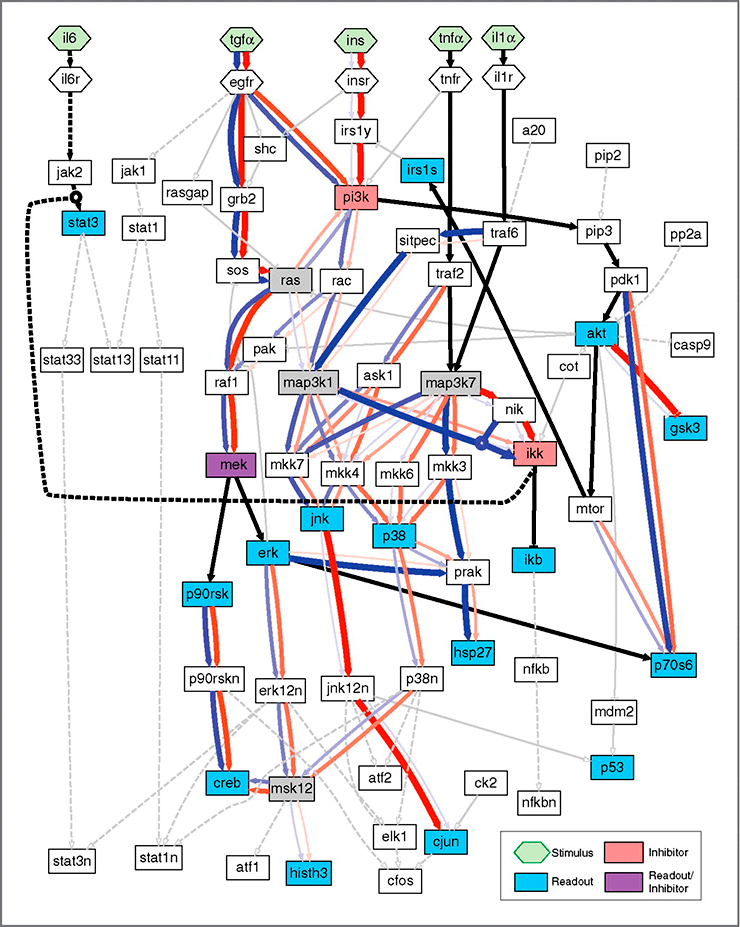
Рисунок 13. Сравнение сигнальной сети первичных гепатоцитов и клеток рака печени (HCC cells). Сигнальные пути первичных гепатоцитов отмечены голубым цветом, а раковых клеток — красным; черным показаны общие сигнальные пути. Тонкие серые дуги соответствуют сигнальным путям, которые отсутствуют во всех моделях. Пунктирные серые линии обозначают дуги, которые были удалены в процессе обучения первичной логической модели. Черная пунктирная линия соответствует дуге, которая изначально отсутствовала в PSN.
Интересным в данном примере является дуга, обозначенная черным пунктиром, соединяющая Ikk и Stat3. При изучении литературных данных исследователи не нашли информации о взаимодействии этих белков. В ходе дальнейших экспериментов выяснилось, что используемый при «обучении» модели химический ингибитор TPCA-1 взаимодействовал не только со своей основной мишенью Stat3, но и с Ikk. Причем это нецелевое взаимодействие даже оказалось более эффективным. Таким образом, с помощью моделирования было установлено, что TPCA-1 впредь можно использовать в качестве эффективного ингибитора Ikk, причем не только в лаборатории, но и в медицинских целях при терапии некоторых видов рака, где задействован Ikk [21], [29].
Как было написано выше, дисрегуляция различных сигнальных путей приводит к различным подтипам рака. Рисунок 14 иллюстрирует отличия в сигнальных путях между различными подтипами рака печени. Таким образом, логическое моделирование может помочь найти индивидуальный подход к терапии рака, что открывает широкие возможности для персонализированной медицины [30].
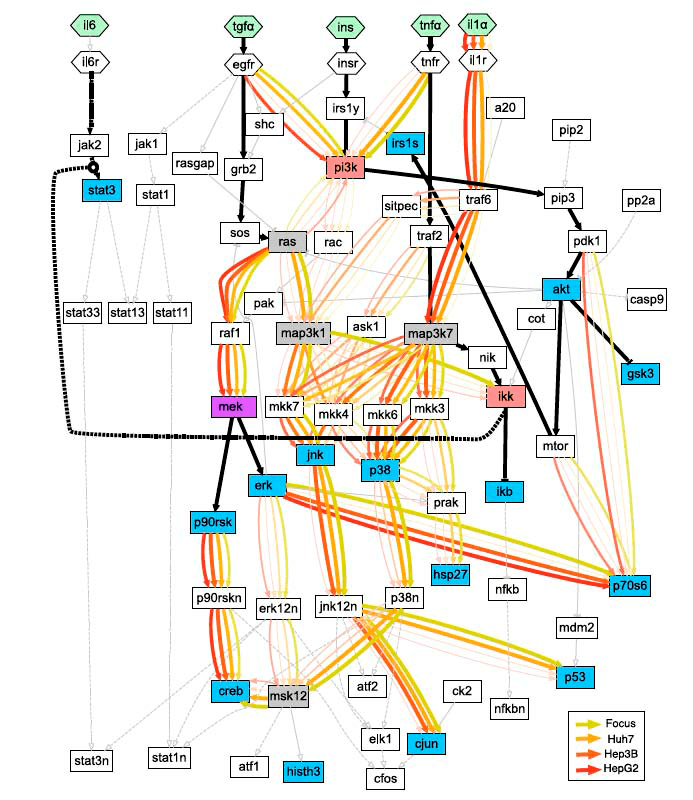
Рисунок 14. Отличия в клеточном сигналинге между различными подтипами рака печени. Обозначения аналогичны таковым на рис. 12.
Моделирование основных сигнальных путей рака простаты
Другим примером логического моделирования клеточного сигналинга является построение модели рака простаты для предсказания вероятности выживания клеток в различных условиях (рис. 15) [2].
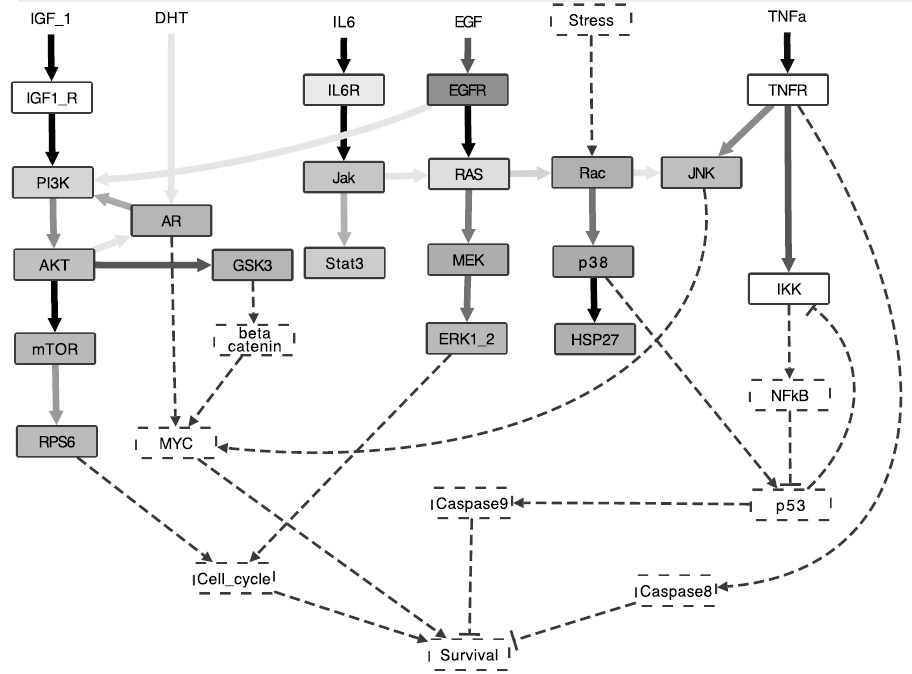
Рисунок 15. Оптимизированная модель основных сигнальных путей при раке простаты. Пунктирными линиями показаны узлы, которые были удалены после компрессии.
Здесь стоит остановиться на важном усовершенствовании при построении модели. Дело в том, что существенным недостатком использования логических операторов является то, что мы работаем с дискретными величинами, которые могут принимать только два значения — 0 или 1. То есть такая «грубая модель» предусматривает только два состояния «включено»/«выключено» для участников сигнальной сети. Здесь можно привести аналогию с лампочкой: мы предсказываем включение или отключение лампочки в ответ на нажатие различной комбинации выключателей. Однако у реальных биологических систем существуют различные переходные состояния, то есть мы должны учитывать силу нажатия на выключатель и «интенсивность свечения» лампочки.
Исследователи в области системной биологии разработали способ перехода от бинарной логической модели к непрерывной модели, которая позволяет преобразовать бинарные значения логического оператора в функцию, область значений которой находится на отрезке [0; 1]. Причем такая модель неплохо работает при описании достаточно больших сигнальных сетей [31].
В этой модели исследовали, как воздействие на разных участников сигнальной сети скажется на выживаемости раковых клеток. С помощью модели удалось оценить вероятность выживания клеток при активации AR- и PI3K-зависимых сигнальных путей. И эти «предсказания» модели находятся в согласии с известными ранее экспериментальными данными [2].
Далее исследователи симулировали ингибирование различных участников сигнальной сети (рис. 16). Модель «предсказала», что ингибирование AKT, MYC и PI3K окажет сильный негативный эффект на выживаемость раковых клеток. И этот результат также согласуется с данными литературы [2].
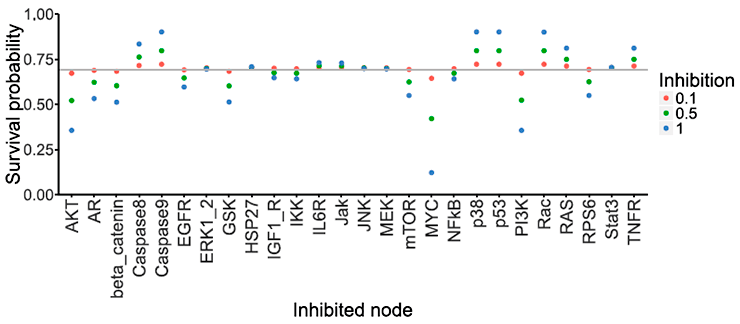
Рисунок 16. Вероятность «выживания» раковых клеток при симуляции ингибирования различных участников сигнальной сети. Вероятность «выживания» в контроле отмечены серой линией.
Тогда исследователи задались вопросом, как на систему может повлиять «коктейль» из различных ингибиторов: будут ли какие-то ингибиторы усиливать эффекты друг друга или наоборот подавлять действие друг друга, и как все это скажется на выживаемости раковых клеток? Например, из рисунка 17 видно, что существует синергизм между Ras- и PI3K-пути, что характеризует их параллельное влияние на фенотип. Таким образом, модель предсказывает, что одновременное влияние на оба этих сигнальных пути сильно скажется на выживаемости клеток.
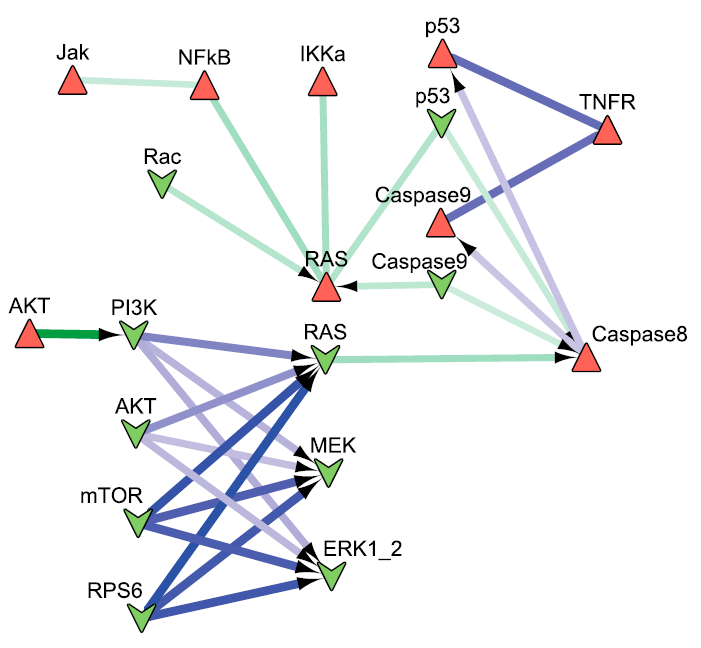
Рисунок 17. Сеть синергетических и антагонистических взаимодействий, рассчитанная со случайными начальными условиями. Красными треугольниками отмечены «активированные» участники, а зелеными глифами — участники, потерявшие свою функциональную активность. Синие дуги обозначают уменьшение вероятности выживаемости, а зеленые дуги — увеличение этой вероятности. Несимметричные взаимодействия показаны стрелками.
Эту схему можно интерпретировать и по-другому. Представим, что на систему не действуют химические агенты, и активация и ингибирование тех или иных участников сигнальной сети достигаются путем генетических нарушений, например, активирующих и инактивирующих мутаций. Таким образом, «прочитав» генетический код пациента, исследователи смогут сопоставить совокупность уникальных генетических нарушений с определенным фенотипом.
Логическое моделирование и персонализированная медицина
Математическое моделирование поведения клетки представляется той технологией, которая может перевернуть наше представление о медицине. Представьте, что пациент приходит к врачу, который делает биопсию и далее строит математическую модель, с помощью которой можно в случае необходимости установить причины заболевания, сделать прогноз о его течении и подобрать необходимый «коктейль» лекарств. На сегодняшний момент лимитирующим фактором является этап сбора материала, так как для обучения модели необходимо довольно большое количество клеток. Относительно недавно разработанная технология ex vivo скрининга образцов ткани пациентов под названием «микрофлюидика» [32] позволяет использовать небольшие объемы препарата для тестирования действия различных лекарств в различных комбинациях. Однако пока с помощью данного метода можно «просчитать» только один узел логической модели [2]. Тем не менее математическое моделирование поведения клетки находит все более широкое применение в области науки под названием «системная фармакология», которая занимается поиском новых лекарственных средств и исследованиями влияния препаратов на системном уровне.
Таким образом, логическое моделирование представляется тем инструментом, с помощью которого можно приоткрыть «черный ящик» под названием «живая клетка», понять, как она функционирует, и использовать эти знания для борьбы с различными заболеваниями.
Литература
- Adria Carbo, Raquel Hontecillas, Tricity Andrew, Kristin Eden, Yongguo Mei, et. al.. (2014). Computational modeling of heterogeneity and function of CD4+ T cells. Front. Cell Dev. Biol.. 2;
- Pauline Traynard, Luis Tobalina, Federica Eduati, Laurence Calzone, Julio Saez-Rodriguez. (2017). Logic Modeling in Quantitative Systems Pharmacology. CPT Pharmacometrics Syst. Pharmacol.. 6, 499-511;
- Junwei Shi, Eric Wang, Joseph P Milazzo, Zihua Wang, Justin B Kinney, Christopher R Vakoc. (2015). Discovery of cancer drug targets by CRISPR-Cas9 screening of protein domains. Nat Biotechnol. 33, 661-667;
- Просто о сложном: CRISPR/Cas;
- CRISPR-эпопея и ее герои;
- Elizabeth Iorns, Christopher J. Lord, Nicholas Turner, Alan Ashworth. (2007). Utilizing RNA interference to enhance cancer drug discovery. Nat Rev Drug Discov. 6, 556-568;
- Есть ли смысл в антисенсах?;
- Обо всех РНК на свете, больших и малых;
- Pavel Neužil, Stefan Giselbrecht, Kerstin Länge, Tony Jun Huang, Andreas Manz. (2012). Revisiting lab-on-a-chip technology for drug discovery. Nat Rev Drug Discov. 11, 620-632;
- 12 методов в картинках: проточная цитофлуориметрия;
- «Омики» — эпоха большой биологии;
- Anirudh Prahallad, Chong Sun, Sidong Huang, Federica Di Nicolantonio, Ramon Salazar, et. al.. (2012). Unresponsiveness of colon cancer to BRAF(V600E) inhibition through feedback activation of EGFR. Nature. 483, 100-103;
- 12 методов в картинках: «сухая» биология;
- In vivo — in vitro — in silico;
- Я б в биоинформатики пошёл, пусть меня научат!;
- Драг-дизайн: как в современном мире создаются новые лекарства;
- Виртуальные тропы реальных лекарств;
- Синтетическая биология: от наблюдения к вмешательству;
- S. Jones, X. Zhang, D. W. Parsons, J. C.-H. Lin, R. J. Leary, et. al.. (2008). Core Signaling Pathways in Human Pancreatic Cancers Revealed by Global Genomic Analyses. Science. 321, 1801-1806;
- Ibiayi Dagogo-Jack, Alice T. Shaw. (2017). Tumour heterogeneity and resistance to cancer therapies. Nat Rev Clin Oncol. 15, 81-94;
- Saez-Rodriguez J. (2011). Logic modeling of cell signaling networks. MIT;
- Julio Saez-Rodriguez, Leonidas G Alexopoulos, Jonathan Epperlein, Regina Samaga, Douglas A Lauffenburger, et. al.. (2009). Discrete logic modelling as a means to link protein signalling networks with functional analysis of mammalian signal transduction. Mol Syst Biol. 5;
- Пространственно-временное моделирование в биологии;
- Как работает свертывание крови?;
- По карте интерактома можно найти неожиданные связи между болезнями;
- Angeloni V.S.S., Cordes R., Dunbar S., Garcia C., Gibson G., Martin C. xMAP Cookbook (1st Edition). Luminex, 2014. — 116 p.;
- Флуоресцентные репортеры и их молекулярные репортажи;
- Steffen Klamt, Julio Saez-Rodriguez, Jonathan A Lindquist, Luca Simeoni, Ernst D Gilles. (2006). . BMC Bioinformatics. 7, 56;
- J. Saez-Rodriguez, L. G. Alexopoulos, M. Zhang, M. K. Morris, D. A. Lauffenburger, P. K. Sorger. (2011). Comparing Signaling Networks between Normal and Transformed Hepatocytes Using Discrete Logical Models. Cancer Research. 71, 5400-5411;
- От медицины для всех — к медицине для каждого!;
- Dominik M Wittmann, Jan Krumsiek, Julio Saez-Rodriguez, Douglas A Lauffenburger, Steffen Klamt, Fabian J Theis. (2009). Transforming Boolean models to continuous models: methodology and application to T-cell receptor signaling. BMC Systems Biology. 3, 98;
- Eduati F., Utharala R., Madhavan D., Neumann U.P., Cramer T., Saez-Rodriguez J., Merten C.A. (2016). Rapid identification of optimal drug combinations for personalized cancer therapy using microfluidics. bioRxiv;
- Burge C., Gifford D., Fraenkel E. (2014). Introduction to computational and systems biology. MIT.